有界函数

在本文中，我们解释什么是有界（上限和下限）函数。此外，我们还将向您展示函数在一点上有界意味着什么，最后您将发现此类函数的属性。

什么是有界函数？

有界函数是其图形在界限内的函数。也就是说，如果存在数字 K 且不存在大于 K (f(x)≤K) 的函数值，则函数在上方有界；如果存在数字 K 使得函数在下方有界，则函数在下方有界小于函数的所有值(f(x)≥K)。因此，有界函数是上下有界的函数。

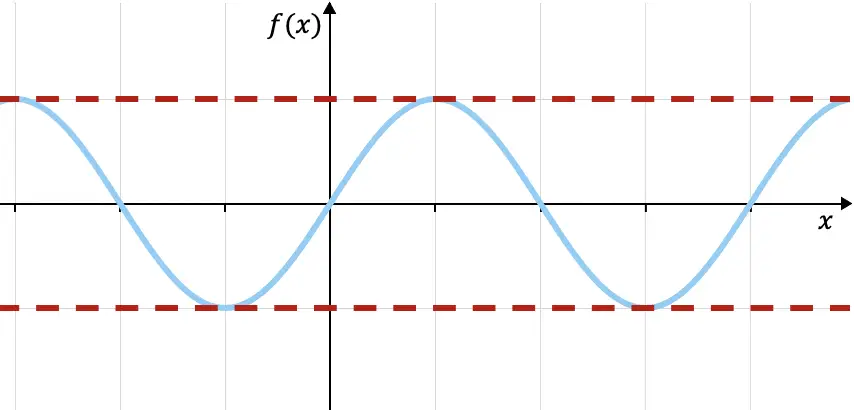
例如，上图所示的三角正弦函数的顶部边界为 f(x)=1，底部边界为 f(x)=-1（红色虚线），因为函数都在这两个限制之内。您可以在以下链接中查看该函数的更多属性：

➤请参阅：正弦函数的特性

上面有界的函数

然而，并非所有函数都有上下界，函数只能有上下界。

上述有界函数是指不超过某个值的函数，即满足以下条件：

其中 K 值是函数的上限。

例如，下面的抛物线在顶部以 K=7 为边界，但该函数在底部没有边界，因为它的分支延伸至无穷大。

从逻辑上讲，如果函数以 K=7 为界，那么它也以 K=8 和更高值为界。

最小的上界称为上界，用sup(f)表示。此外，如果函数在其定义域中达到所述上限，我们会说该点是函数的绝对最大值。

➤看： 函数的最大值和最小值是多少？

在我们的例子中，函数的几何边界为 K=7，因此它是函数的上极值和绝对最大值。

下面分隔的函数

下面界定的函数是那些值不小于某个数字的函数，即它们满足以下数学表达式：

其中K值是函数的下界。

下面是指数函数的图形表示，下面用 K=3 分隔：

显然，该函数也受到小于 K=3 的值的限制。

如前所述，最大下界称为下界，用inf(f)表示。此外，如果函数在其定义域中达到所述下极值，我们会说该点是函数的绝对最小值。

在这种情况下，K=3 不是函数的绝对最小值，因为函数在无穷远处达到该值，因此它在其域之外。换句话说，f(x)=3 是函数 的水平渐近线。

有一个定理可以让您知道函数是否在顶部和底部有界，而无需其图形表示。单击此处查看维尔斯特拉斯定理是什么。

➤参见： 维尔斯特拉斯定理

函数有界于一点

我们刚刚研究了一般函数有界的概念，但也可以分析函数是否在较小的邻域内（即函数的一部分）有界。

是的

是函数域中的一个点并且

任何值，我们都会说该函数在该点的上方/下方有界

如果有一个环境

其中函数在上方/下方有界。

因此，函数有界于点

如果它是在邻域的顶部和底部界定的

显然，如果一个函数总体上是有界的，那么它在它的每个点上也将是有界的。然而，相反的情况是错误的，也就是说，函数可以在其每个点上有界，但不能在其整个域上有界。

例如，以下仿射函数在其每个点处都有部分有界，但它不是有界函数。

有界函数的性质

有界函数具有以下性质：

• 是的

  

  和

  

  是两个有界函数，两个函数的加（或减）

  

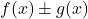
  也是有界函数。

• 是的

  

  和

  

  是两个有界函数，两个函数的乘积

  

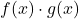
  也恰好是一个有界函数。

• 如果函数有垂直渐近线，则它不能完全有界。另一方面，函数可以在上方或下方有界。
• 区间上的任何连续且有界的函数都是可积的。