在这里您将发现什么是有理函数。此外,我们还解释了如何计算有理函数的域和渐近线。不仅如此,您还会看到有理函数的所有特征是什么。最后,您可以逐步练习有理函数。
什么是有理函数?
有理函数的定义如下:
有理函数是由两个多项式的商形成的函数,也就是说,有理函数是分子和分母中都有多项式的分数。
有理函数的特征是在分母消失的点处存在奇点。
![]()
有理函数也称为分数函数。
另一方面,有理函数不应与无理函数混淆。无理(或激进)函数是由根组成的函数。
有理函数的例子
为了更好地理解有理函数的概念,我们将看到此类函数的几个示例。
- 分子和分母为一次多项式的有理函数:
![]()
这些类型的有理函数也称为单应函数。
- 分子为常数、分母为多项式的有理函数:
![]()
这些类型的有理函数称为反比例函数,用于在数学上定义反比例量。
- 分子为三次多项式、分母为二次多项式的有理函数:
![]()
有理函数的域
一个数除以 0 是一个不确定性,它给出无穷大 (∞),因此除非分母为 0,否则有理函数将始终存在。
因此,有理函数的域由除分母相消的值之外的所有实数组成。
因此,要获得有理函数的定义域,我们需要找到分母何时为 0,因为这一点将是唯一不属于该定义域的点
让我们通过求解一个例子来看看如何计算有理函数的域:
![]()
我们首先将分母设置为 0,然后求解所得方程:
![]()
![]()
因此,当x为-2时,分母将为0,因此该函数将不存在。因此,函数的域由除 x=-2 之外的所有实数组成。声明如下:
![]()
有理函数的渐近线
有理函数的主要属性之一是它们的渐近线,因为它们决定了它们的图形表示。
➤请参见:函数的图形表示
有理函数的渐近线是函数图形无限接近但从未接触的线。
渐近线有三种类型:垂直渐近线、水平渐近线和倾斜渐近线。
下面是有理函数可以用红色绘制的三种类型的渐近线。
有理函数的垂直渐近线

有理函数的水平渐近线

有理函数的斜渐近线

正如您所看到的,从函数的图形确定函数的渐近线非常简单,但是在没有图形表示的情况下计算有理函数的渐近线则相当复杂。这就是为什么我们建议您在我们的网站上了解如何计算函数的渐近线。
有理函数的特征
有理函数具有以下特点:
![]()
- 正如我们在上面看到的,有理函数的域包括除消除分数分母的值之外的所有实数。
- 一般来说,有理函数的值域(或范围)包括除函数具有水平渐近线的值之外的所有实数。
- 有理函数在其整个域内是连续的。或者换句话说,有理函数在不属于其定义域的点处表现出不连续性。
- 大多数有理函数的图形表示由两条双曲线组成。
- 有理函数渐近线的一些规则可以从多项式分子推导出来。

和分母多项式
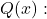
- 有理函数在作为根的点处有一条垂直渐近线

但这些不是根源
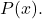
- 如果程度

的程度小于

,线 y=0 是有理函数的水平渐近线。
- 如果程度

大于的程度

,有理函数没有水平渐近线。
- 如果程度

是一个大于度数的单位

并且两个多项式没有共同根,有理函数有斜渐近线。
- 有理函数在作为根的点处有一条垂直渐近线
解答了有理函数的练习
练习1
求以下有理函数的域:
![]()
它是一个有理函数,因此定义域由除分母相消的数字之外的所有数字组成,因为这样该函数将给出 ∞。
所以我们将整数分母设置为零,看看哪个数字不属于该域:
![]()
我们求解所得方程:
![]()
![]()
因此,函数的定义域仅由除 -2 之外的数字组成:
![]()
练习2
找到以下有理函数与笛卡尔轴的截止点:
![]()
X轴切削点
为了找到函数与 X 轴的交点,需要求解
![]()
![]()
![]()
![]()
![]()
![]()
![]()
我们得到了二次方程的两个解,因此有理函数与横坐标轴相交于两个不同的点,即:
![]()
Y轴切削点
要找到与 Y 轴的交点,您必须计算
![]()
![]()
任何数字除以零都是不确定的,会得到无穷大。因此,有理函数不会经过Y轴上方的任何点,即与y轴没有交点。
练习3
在图上绘制以下有理函数:
![]()
首先要做的是计算函数的域:
![]()
![]()
![]()
![]()
一旦我们知道了函数的域,我们就构建一个值表:

最后,只需在图表上表示获得的点并绘制双曲线,从而绘制有理函数:

练习4
确定下图有理函数的渐近线:
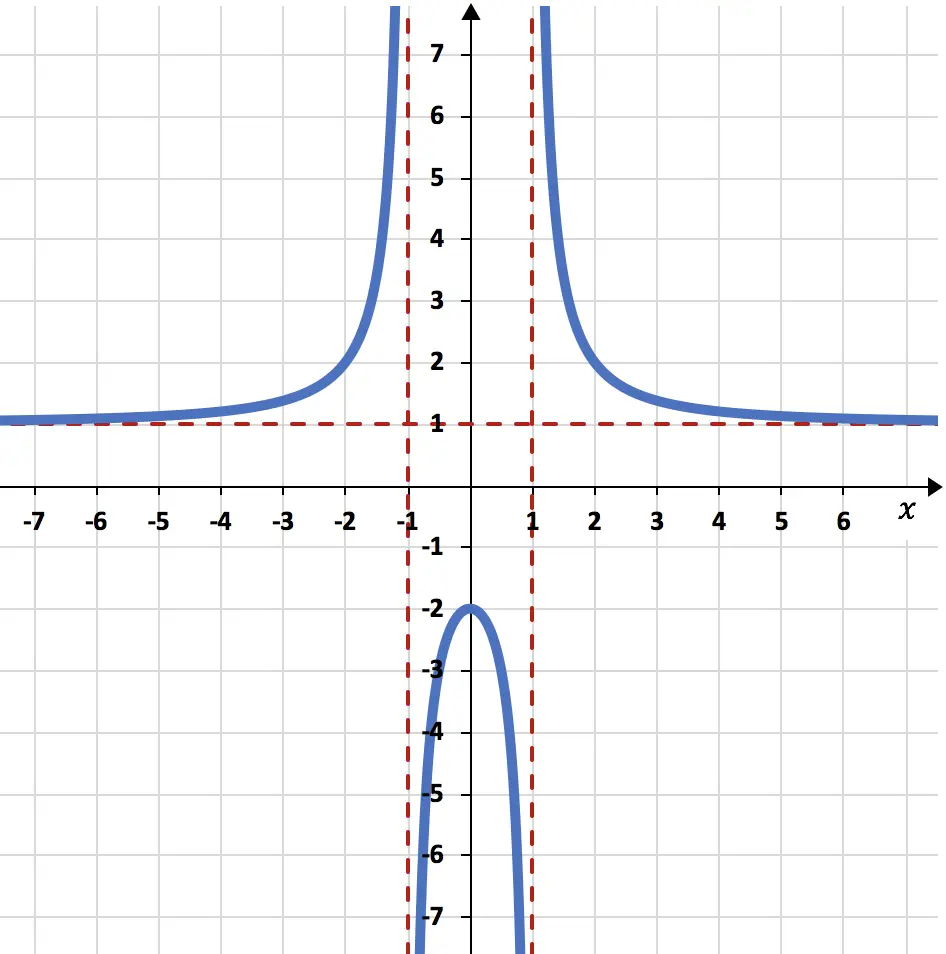
渐近线在图表上非常清晰可见,因为它们表示为红色虚线。
在这个问题中,函数非常接近水平线 y=1,但从未触及它。因此,有理函数有一个水平渐近线,即 y=1。
同样,函数的图形表示非常接近垂直线 x=-1 和 x=1,但从未达到这些值。因此,有理函数有两个不同的垂直渐近线,即 x=-1 和 x=1。
练习5
计算以下有理函数的所有渐近线:
![]()
注意:要解决此练习,我们建议您首先访问上面有关如何计算函数渐近线的链接并查看说明。
垂直渐近线
要计算函数的垂直渐近线,我们必须首先找到函数的定义域。因此,我们将有理函数的分母设置为0来查找不属于域的点:
![]()
![]()
![]()
因此,函数的域由除 -1 之外的所有数字组成:
![]()
所以 x=-1 可能是垂直渐近线。为了检查这一点,我们必须计算函数在该点的极限:
![]()
因此,x=-1 是有理函数的垂直渐近线,因为此时函数的极限给出无穷大。
水平渐近线
为了确定水平渐近线,我们需要计算函数的无限极限:
![]()
![]()
在这种情况下,无穷大之间的不确定无限极限的结果是最高次 x 的系数的除法,因为分子和分母具有相同的阶数。
该函数的两个无限极限给了我们 3,因此 y=3 是有理函数的水平渐近线。
斜渐近线
由于有水平渐近线,有理函数没有斜渐近线。