在这里,您将了解什么是函数的凹性和凸性,以及如何判断函数是凹函数还是凸函数。此外,您还可以逐步练习函数曲率。
什么是函数的凹性和凸性?
函数的凹性和凸性是指函数图形的曲率。凹函数是图形具有山形状的函数,凸函数是图形具有山谷形状的函数。
上一段为了便于理解,对凹函数和凸函数进行了非正式的定义,但凹函数和凸函数的数学定义如下:
- 凹函数:当函数任意两点相连的线段在曲线下方时。
- 凸函数:当函数任意两点相连的线段位于曲线上方时。
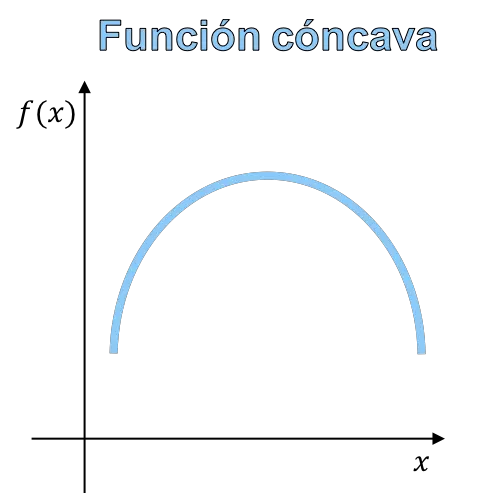

最终,凹函数和凸函数之间的区别在于函数的形状,因此,您可以从函数的图形中区分凹函数和凸函数。
然而,函数不一定在其整个域上是凹函数或凸函数,也可以在一个区间上是凹函数,在另一个区间上是凸函数。
注意:数学界仍然没有完全同意,因此,一些教授提出了相反的说法:他们将形状为 a 的函数称为凹函数
![]()
,以及一个凸函数,其形式为
![]()
。无论如何,重要的是知道函数是什么,无论名称如何。
如何研究函数的曲率
研究函数的曲率涉及求函数的凹凸性,即知道函数凹的区间和凸函数的区间。
因此,要研究函数的曲率,必须执行以下步骤:
- 找出不属于函数定义域的点。
- 计算函数的一阶导数和二阶导数。
- 求二阶导数的根,即通过求解计算抵消二阶导数的点
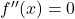
。
- 用导数的根和不属于函数定义域的点建立区间。
- 计算每个区间中某个点的二阶导数值。
- 因此,二阶导数的符号决定了该区间内函数的凹性或凸性:
- 如果函数的二阶导数为正,则函数在此区间上是凸函数。
- 如果函数的二阶导数为负,则函数在此区间上是凹函数。
如何求函数曲率的示例
接下来,我们将逐步求解一个示例,以便您了解如何计算函数的凹凸区间。
- 研究以下函数的凹凸性:
![]()
首先要做的是计算函数的定义域。在这种情况下,我们有一个多项式函数,因此函数的域由实数组成:
![]()
一旦我们计算了函数的域,我们就需要研究函数的二阶导数在哪些点消失。
因此,我们计算函数的一阶导数:
![]()
然后我们求函数的二阶导数:
![]()
现在我们将二阶导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
一旦我们计算了函数的域并且
![]()
,我们代表线上找到的所有关键点。在这种情况下,我们在计算函数定义域时没有找到任何临界点,但我们得到了一个抵消函数二阶导数的点:
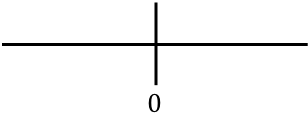
现在我们评估每个区间内的二阶导数的符号,以了解该函数是凹函数还是凸函数。因此,我们在每个区间取一个点(而不是临界点),并查看此时二阶导数的符号:
![]()
![]()
![]()

最后,我们推导出函数的凹凸区间。如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此函数的凹凸区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
解决了函数的凹性和凸性练习
练习1
计算以下多项式函数的凹凸区间:
![]()
练习中的函数是多项式,因此函数的域由实数组成:
![]()
确定函数的定义域后,我们对其进行微分:
![]()
然后我们求函数的二阶导数:
![]()
现在我们将二阶导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
一旦我们计算了函数的域并求解
![]()
,我们表示数轴上找到的所有奇异点:

现在让我们取一个属于每个区间的点,看看此时的二阶导数是什么符号:
![]()
![]()

当二阶导数大于零时,表示函数是凸函数。
![]()
,但是当二阶导数为负时,这意味着该函数是凹函数
![]()
。因此,凹凸区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
练习2
研究以下有理函数的曲率:
![]()
首先我们需要计算函数的域。由于这是一个有理函数,我们将分母设置为零,看看哪些数字不属于函数的域:
![]()
![]()
![]()
![]()
这意味着当x为-2或+2时,分母将为0。因此,该函数将不存在。因此,函数的域由除 x=-2 和 x=+2 之外的所有数字组成。
![]()
其次,我们计算函数的一阶导数:
![]()
![]()
然后我们求解二阶导数:


所有项均乘以
![]()
。因此我们可以简化分数:

![]()
![]()
![]()
![]()
现在我们来计算函数二阶导数的根:
![]()
![]()
期限
![]()
这涉及到将整个左侧除,因此我们可以将其乘以整个右侧:
![]()
![]()
我们提取公因数:
![]()
为了使乘法等于 0,乘法的两个元素之一必须为零。因此,我们将每个因子设置为0:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
没有解,因为实数没有负根。
现在我们在线上表示所有获得的临界点,即不属于定义域的点(x=-2 和 x=+2)以及取消二阶导数的点(x=0):

我们评估每个区间内的二阶导数的符号,以了解该函数是凹函数还是凸函数。因此,我们在每个区间中取一个点,看看该点的二阶导数的符号是什么:
![]()
![]()
![]()
![]()

如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此,凹度和凸度区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
练习3
一个功能
![]()
具有相对极端的
![]()
。更重要的是,该函数是凸函数
![]()
在同一点上。确定相对极值是最小值还是最大值。
➤请参阅: 函数最大值和最小值的定义
设凸函数
![]()
在
![]()
表示此时的二阶导数为正,即
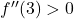 因此,相对极端
因此,相对极端
![]()
这是最小值,因为
![]()
这是积极的。