不可约分数是不能进一步简化的分数,因此它没有更小的等价分数。换句话说,不可约分数的分子和分母的 gcf 等于 1,因为它们没有其他公约数。例如,表达式“5/8”不能再约简,所以我们说它是最简单的形式或者说它是不可约的。
不可约分数计算器
在继续理论之前,我们想向您展示一个计算器,它可以让您获得任何混合数的不可约分数。您所要做的就是输入分子和分母的值,然后单击“简化分数” ,您将在结果框中获得简化形式。我们建议使用此工具立即简化任何分数,甚至纠正您的分数练习。
什么是不可约分数以及它是如何计算的?
正如我们在开始时已经解释的那样,不可约分数是不能进一步简化的分数,因此它是立即分数。如果你想找到这种类型的分数,你将不得不使用分数的化简,这样你就会找到一个相对于初始分数不可约的等价分数。在最后一个链接中,您可以找到有关简化分数的详细指南,尽管在下面的列表中我们以摘要方式解释了这些步骤:
- 查找公因数:首先,您需要找到分子和分母的最大公因数。这样你就得到了一个数字,可以让你在保持相等的同时减少这两个值。
- 将可约分数除以 gcf:获得 gcf 后,您需要将分子和分母除以该公约数。这将为您提供更简单(或更小)的等效分子和分母。
您还可以使用其他方法来查找不可约分数,这在我们有关化简分数的文章中进行了解释。尽管通过我们向您解释的这种方法,您可以非常轻松快速地减少您想要的任何分数。
可约分数和不可约分数的示例
在下图中,您可以找到四个可约分数的示例和另外四个不可约分数的示例。我们建议您尝试简化每个分数,这样您就会清楚地了解两种分数之间的区别。
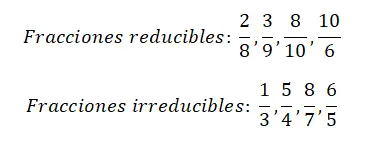
计算不可约分数的示例
在这里,我们逐步向您展示如何使用两种方法简化分数。第一个显示了我们在上一节中解释的完整过程。第二个显示了一个稍微不同的系统,它涉及将分子和分母除以相同的值,从最小的除数(不包括 1)开始,然后依次进行。不过,如果你觉得第二个系统太复杂,可以忽略它。
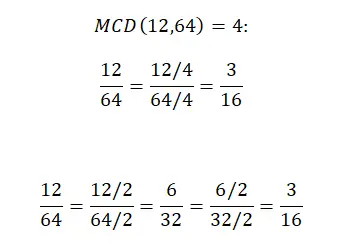
小数的不可约分数
从小数得到的不可约分数称为生成分数。值得注意的是,它的计算方式不同,具体取决于我们处理的小数类型(精确、纯周期或混合周期)。下面的例子清楚地展示了这个数学概念: 5/7 = 0.7142857... 如您所见,七分之五是相当于十进制数 0.7142857... 的不可约分数...
你怎么知道分数是否是不可约的?
要确定分数是可约还是不可约,可以采用两种方法。第一个是计算分子和分母的最大公约数,如果该值与 1 不同,则意味着它是可约分数。如果你得到一个结果,你就知道这个分数是不可约的。其次,您可以使用我们在开始时向您展示的不可约分数计算器来执行这些类型的检查。
解决了不可约分数的练习
现在您已经阅读了理论,我们建议您尝试解决这些问题,这将使您能够练习计算不可约分数。此外,如果您想提高对带分数的理解,我们建议尝试解决这些分数练习。通过它你将更好地理解分数本身的概念。
练习1
计算下列可约分数的不可约分数。请记住,您可以使用任何方法来简化分数。当您完成练习后,您可以将您的结果与我们在下图中向您展示的结果进行比较。
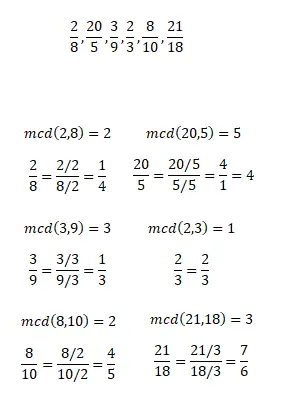
练习2
识别与不可约分数 2/3 和 4/5 等价的分数。为了完成此任务,我们建议查看分子和分母中的数字,并思考它们之间的整除关系。也许你可以使用最大公因数或最小公倍数来找到你要找的东西......
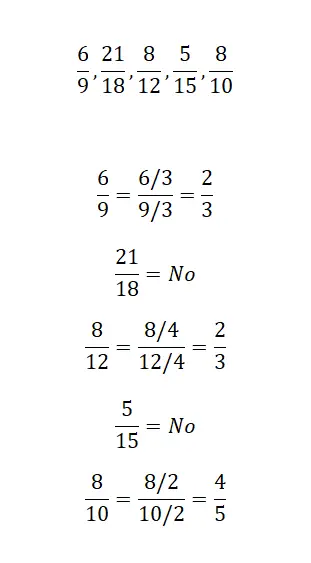
练习3
在最后一个练习中,您只需指出以下三个分数是否具有相同的不可约分数。因此,有必要尽可能地减少这三个分数并分析结果。一旦您解决了该问题,您就可以将您的解决方案与我们的解决方案进行比较。
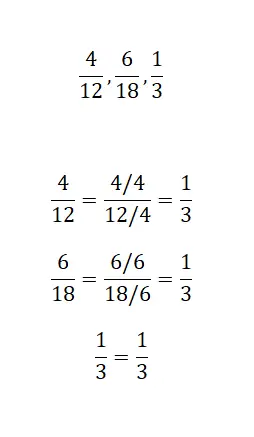
有关分数的更多信息
我们希望本文能帮助您理解不可约分数。不过,如果您有任何疑问,请随时阅读我们对分数的解释。在那里,您将找到有关分数的所有信息:定义、类别、运算和练习,所有信息均使用理论和示例进行解释。我们向您保证,如果您阅读本文,您将消除与该主题相关的许多基本疑虑。