斜渐近线

在本文中，我们解释什么是函数的斜渐近线。您将了解函数何时具有斜渐近线以及如何计算它。此外，您还可以看到斜渐近线的示例，并通过逐步解决的练习进行练习。

什么是斜渐近线？

函数的斜渐近线是一条斜线，其图形无限接近且不会与其相交。因此，所有斜渐近线都是符合方程y=mx+n 的线。

斜渐近线的斜率和原点使用以下公式计算：

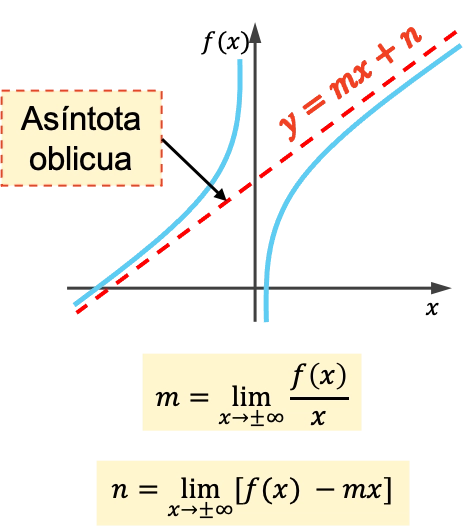
如何计算函数的斜渐近线

要计算函数的斜渐近线，必须执行以下步骤：

1. 计算函数除以 x 的无穷大极限。
2. 如果上述限制导致非零实数，则意味着该函数具有斜渐近线。而且，所述斜渐近线的斜率将是在极限处获得的值。



3. 在这种情况下，剩下的就是通过求解以下极限来计算斜渐近线的截距：

注意：极限必须在正无穷大和负无穷大处计算，但它们通常给出相同的结果，这就是为什么我们通过输入±无穷大来简化。但如果正无穷大和负无穷大的极限不同，则必须分别计算左斜渐近线和右斜渐近线。

斜渐近线示例

接下来，我们将采用以下有理函数的斜渐近线，以便您可以看到如何完成此操作的示例：

斜渐近线的类型为

所以我们首先计算直线的斜率

及其相应的公式：

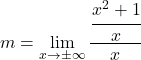
为了解决这个限制，我们必须应用分数的性质：

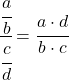
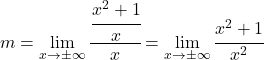
现在我们计算极限：

在这种情况下，无穷大之间的无穷大不确定性的结果是最高次 x 的系数相除，因为分子和分母具有相同的阶数。

上面的极限给出了一个非零实数，因此该函数有一个斜渐近线。我们现在将计算 y 轴截距

使用相应的公式计算渐近线：

我们尝试计算极限：

但我们得到不确定性无穷大减去无穷大。因此，有必要将这些术语简化为一个公分母。为此，我们将 x 除以分数的分母：

现在这两项具有相同的分母，我们可以将它们分组：

我们对分子进行运算：

最后，我们解决了限制：

所以n =0。因此，斜渐近线是一个线性函数：

研究的函数如下图所示。正如您所看到的，该函数非常接近线 y=x，但从未触及它，因为它是斜渐近线：

已解决斜渐近线练习

练习1

求以下有理函数的斜渐近线：

斜渐近线的形式为

，因此需要计算参数m和n 。我们首先通过应用其公式来计算m ：

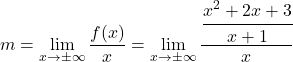
我们通过应用分数的性质来简化分数：

我们解决极限：

所以m =1。现在让我们应用公式计算斜渐近线的截距：

我们尝试计算极限：

但我们得到了无穷大减去无穷大的不定形式。因此，我们必须将这些项简化为一个公分母，然后将它们分组：

最后，我们解决了限制：

简而言之，函数的斜渐近线为：

练习2

找出以下有理函数的所有斜渐近线：

首先，我们使用斜渐近线的斜率公式：

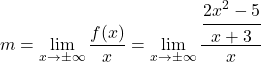
我们通过应用分数的性质来简化分数：

我们确定极限：

极限给出非零的实数，因此它是一个斜渐近线的有理函数，其斜率为 2。

现在让我们通过应用相应的公式来计算截距：

我们尝试计算极限：

但我们得到了无穷大的差不确定性。因此，我们将各项简化为公分母，然后进行运算：

最后，我们解决了限制：

综上所述，分数函数的斜渐近线为：