本页解释什么是数字的阶乘及其计算方法。此外,还提供了几个示例和一个包含最常用阶乘值的表格。它还教授如何使用计算器计算数字的阶乘。最后,说明了阶乘的应用和性质。
一个数的阶乘是什么?
在数学中,数字的阶乘等于从 1 到该数字的所有正整数的乘积。此外,数字的阶乘由数字后面的感叹号 (!) 表示。
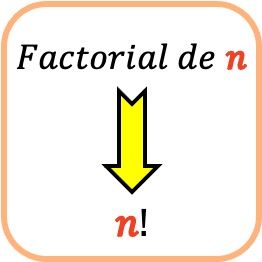
例如,要确定数字n的阶乘(也称为阶乘n ),您必须将数字n乘以它前面的所有整数(从 1 开始):
![]()
如何计算数字的阶乘
一旦我们了解了数字阶乘的含义,让我们通过一个例子来看看如何确定任何阶乘:
- 计算 4 的阶乘:
正如我们在其数学定义中看到的那样,数字的阶乘相当于所有小于或等于该数字的正整数的乘积。因此,要计算 4 的阶乘,我们需要将数字 1、2、3 和 4 相乘:
![]()
因此 4 的阶乘得到 24。
数字的阶乘示例
为了完成对数字阶乘概念的理解,我们给您提供一个计算不同数字的阶乘的示例:
- 3 的阶乘:
![]()
- 5 的阶乘:
![]()
- 6 的阶乘:
![]()
- 1 的阶乘:
![]()
从逻辑上讲,数字 1 的阶乘等于 1,因为乘以 1 就足够了。
- 0 的阶乘:
![]()
是的,好吧,令人惊讶的是,0 的阶乘不等于 0,而是等于 1。这对你来说可能有点奇怪,因为理论上你必须将 0 乘以 1。但是,按照惯例,0! =1,因为产品属性为空。我们给您留下这个链接,以防您想了解更多信息,尽管您知道原因并不真正相关,但重要的是您记住0 的阶乘等于 1 。
数字阶乘的结果列表
下面我们在表格中总结了最常用数字的阶乘,因此您不必手动计算它们。
| 号码 | 数字的阶乘 |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5,040 |
| 8 | 40,320 |
| 9 | 362,880 |
| 十 | 3,628,800 |
| 十一 | 39,916,800 |
| 12 | 479,001,600 |
| 13 | 6,227,020,800 |
| 14 | 87 178 291 200 |
| 十五 | 1,307,674,368,000 |
| 16 | 20,922,789,888,000 |
| 17 号 | 355,687,428,096,000 |
| 18 | 6,402,373,705,728,000 |
| 19 | 121,645,100,408,832,000 |
| 二十 | 2,432,902,008 176,640,000 |
| 五十 | 3,041,409,320 · 10.64 |
| 100 | 9,332 621,544 · 10,157 |
| 1,000 | 4,023,872,601· 10.2567 |
| 10,000 | 2,846,259,681 · 10,35,659 |
| 100,000 | 2 824 229 408·10 45 6573 |
| 1,000,000 | 8,263,931,688·10 5,565,708 |
用计算器计算数字的阶乘
正如您在前面的示例中所看到的,两个连续数字的阶乘结果呈指数级增长,这就是为什么要知道大数的阶乘相当困难。因此,我们将向您展示如何使用计算器求数字的阶乘。
科学计算器有一个带有x 符号的键!或n!用于计算整数的阶乘。因此,要确定阶乘的价值,您必须在计算器上执行以下序列:
![]()
通常,CASIO 计算器有阶乘键 x!或n! x -1按钮上方。
例如,我们将使用计算器求解阶乘,以便您可以检查您是否知道如何执行此操作。例如,我们将计算 9 的阶乘:
![]()
要求 9 的阶乘,必须先输入数字 9,然后按 键
![]()
最后,按等于按钮。在这种情况下,计算器应该向我们显示结果 362,880。
阶乘数的应用
数字的阶乘函数可能看起来是一个非常简单和荒谬的运算,但在高级代数中它被大量使用。然后我们将看到阶乘的主要用途。
首先,阶乘是计算组合数的基本运算,是一种更特殊的运算。如果您不知道组合数是什么,您可以在此链接中查看它的组成以及它的计算方式,您可以在其中找到示例、已解决的练习及其属性。此外,您将能够看到它的用途,因为它有许多实际应用程序。
阶乘还在数学中用于确定函数的泰勒多项式。
同样,阶乘用于解决某些组合问题,特别是计算组合和排列。从这个意义上说,阶乘也经常用于使用组合数学来计算概率。
n 个元素的排列对应于可以用这些元素进行的每种不同排列。因此,为了计算排列,需要使用阶乘。例如,如果在一个问题中您想要找到 7 个对象可以排列的可能性数量,则必须计算 7 的阶乘。
现在让我们看一个已解决的练习:
- 我们有 5 双不同的鞋子,我们有多少种排列方式?
在这个练习中,我们必须考虑到我们放置这 5 双鞋的顺序,找出所有可能的组合方式。因此,要解决这个问题,您只需计算 5 的阶乘:
![]()
简而言之,5双鞋可以有120种不同的摆放方式。
阶乘数的性质
阶乘数具有以下特点:
- 为两个正整数n和m且n大于m ,则显然n的阶乘值大于m的阶乘值。
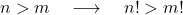
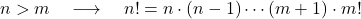
![]()
- 以下代数表达式对于任何数字的阶乘都有效,但 1 的阶乘除外:
![]()
负数或小数的阶乘
我们刚刚看到了如何求正整数的阶乘值,但是……我们可以计算负数或小数的阶乘吗?答案是肯定的,但需要先进的数学知识。
负数和小数的阶乘是使用称为欧拉“伽玛函数”的特殊函数计算的,该函数由以下积分定义:
![]()
因此,任何类型的阶乘都可以使用 Gamma 函数求解,因为以下方程始终为真:
![]()
例如,要找到 0.5 的阶乘,我们必须找到
![]()
因为:
![]()
积分的解将对应于 0.5 的阶乘。
显然,求解 Gamma 函数的积分并不容易,我们在本文中不会教授它,因为许多数学概念必须事先解释。但我们想让您知道,可以计算负数或小数的阶乘。
事实上,作为一个例子,我们计算了一些负的阶乘和小数值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|