在此页面上,您将找到总和平方的公式,即著名的恒等式 (a+b) 2 。您还可以看到平方和的示例和已解决的练习。而且,更重要的是,您会发现隐藏在这款非凡产品中的几何特性。
总和的平方是多少?
和的平方是值得注意的恒等式(或值得注意的乘积)之一,因此它是一种数学规则,可让您快速计算具有两个正项平方的二项式的幂。
因此,和的平方由两个不同的项相加并平方而成,即和的平方的代数表达式为(a+b) 2 。
总和的平方公式
给定这种非凡类型的恒等式的数学定义,我们现在将了解总和平方的公式是什么:

因此,总和的平方等于第一项的平方,加上第一项与第二项乘积的两倍,再加上第二项的平方。
因此,要求解平方和,将每个加法增加到 2 是不够的,此外,还必须将两个加法相乘并乘以 2。
记住这一点很重要,因为在添加平方时一个非常常见的错误是忘记两项之间的乘积而只计算平方:

请记住不要在公式中遗漏任何项!
另一方面,请记住,平方减法(或减法的平方)的公式与我们刚刚看到的公式非常相似,但它有一个差异,完全改变了结果。如果您不确定它是什么样的,您可以在此处查看平方减法公式是什么及其应用方式。
平方和的示例
以下是几个实际示例,您可以了解如何求和的平方:
实施例1
- 应用以下公式计算以下平方和:
![]()
平方和的公式为:
![]()
我们首先要确定参数
![]()
和
![]()
的公式。在这种情况下,
![]()
代表
![]()
的对和
![]()
对应数字5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
好吧,既然我们现在知道了
![]()
和的
![]()
我们可以应用以下公式求出总和平方的结果:

实施例2
- 求解以下表达式以获得总和的平方:
![]()
总和平方的公式为:
![]()
那么在这个问题中
![]()
是单项式
![]()
另一方面,
![]()
是独立项 4:
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
最后,一旦我们确定了
![]()
和的
![]()
,我们应用平方和公式来求解显着乘积:
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
总和平方公式的证明
然后我们会从和的平方推导出刚才看到的公式,这样你就明白它是从哪里来的。
从正二项式开始到 2:
![]()
上面的幂显然就等于因子
![]()
乘以自身:
![]()
因此,我们使用分配律将两个括号相乘:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
最后,根据结果术语,我们将相似的术语分组:
![]()
并且我们已经得到了该公式的多项式表达式,因此证明:
![]()
尽管可能难以置信,但求和公式的平方也适用于二次多项式因式分解。如果您不知道它是什么,多项式因式分解是数学中经常用于简化多项式表达式的过程。单击上面的链接了解其操作方法。
总和平方的几何解释
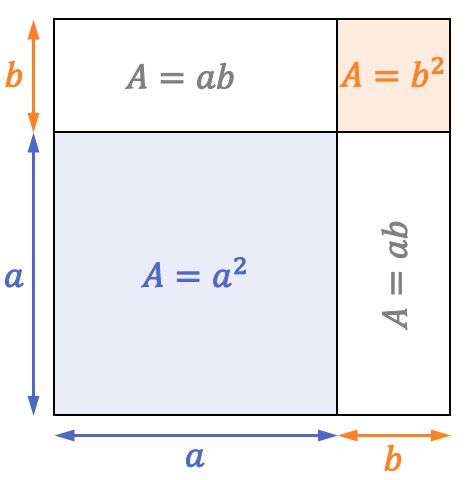
到目前为止,我们已经了解了如何用数学方法计算总和的平方,但这个非凡的乘积也可以用几何方法来解释。
看下面的正方形,其边长是多少
![]()
正方形的面积等于其一条边的长度的平方。因此,由于前一个正方形的边是
![]()
它的面积(或表面积)等于
![]()
嗯,正如您在正方形表示中看到的,面积为
![]()
有两个区域的矩形
![]()
和另一个正方形的表面
![]()
因此,从几何角度来看,平方和的公式也成立:
![]()
解决了总和的平方问题
然后,我们给您提供几个已解决的平方和逐步练习,以便您可以练习并从而完成对概念的理解。您可以在评论中写下您的所有问题,我们将很乐意回答。 💭💭💭
练习1
确定以下平方和:
![]()
![]()
![]()
![]()
为了解决问题的所有显着恒等式,应用总和平方公式就足够了:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
练习2
应用以下公式求解以下两项的平方和:
![]()
![]()
![]()
要计算问题的所有显着乘积,您必须使用平方和公式:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
在 B) 部分中,您需要记住,如果根是平方的,则它会被简化:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
最后一个平方和的单项式有分数系数,因此要解决它,我们还需要使用分数的性质:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
练习3
通过应用总和平方公式计算以下幂,无需使用计算器:
![]()
首先,数字十七可以分解为10加7的和:
![]()
所以我们将功率转换为平方和。因此,我们现在可以应用相应的公式:
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
简而言之,增强的结果是:
![]()
正如您在本练习中看到的,平方和公式对于在不使用计算器的情况下计算大数的幂也很有用。
三项之和的平方
有时我们可能会发现我们需要求解三个相加项的平方,即 (a+b+c) 2 。从逻辑上讲,在这些情况下我们不能使用我们解释的公式,因为括号内有一个三项式而不是二项式。因此有必要使用不同的公式。
3项之和的平方公式如下:
![]()
让我们通过一个例子来看看这个公式是如何应用的:
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
正如您所看到的,向公式中添加一个元素会使结果变得更加复杂。