鲁什-费贝尼乌斯定理

在本页中，我们将了解什么是Rouché Frobenius 定理以及如何用它计算矩阵的秩。您还将找到使用鲁什-弗罗贝尼乌斯定理逐步解决的示例和练习。

什么是鲁什-弗罗贝尼乌斯定理？

鲁什-弗罗贝尼乌斯定理是一种对线性方程组进行分类的方法。换句话说，鲁什-弗罗贝尼乌斯定理用于找出方程组有多少个解，而无需求解它。

方程组有 3 种类型：

系统兼容确定（SCD）：系统具有独特的解决方案。
不确定兼容系统（ICS）：系统有无限个解。
系统不兼容（SI）：系统无解决方案。

此外，鲁什-弗罗贝尼乌斯定理稍后也将允许我们使用克莱默规则来求解系统。

鲁什-弗罗贝尼乌斯定理的陈述

鲁什-弗罗贝尼乌斯定理指出

$\displaystyle \bm{A}$

是由方程组的未知数的系数形成的矩阵。和肚子

$\displaystyle \bm{A'}$

或扩展矩阵是由方程组的未知数和独立项的系数形成的矩阵：

鲁什-弗罗贝尼乌斯定理让我们能够根据矩阵 A 和 A’ 的秩知道我们正在处理什么类型的方程组：

如果rank(A)=rank(A’)=未知数⟶确定的兼容系统(SCD)
如果rank(A)=rank(A’)<未知数⟶不确定兼容系统(SCI)
如果范围(A)
$\bm{\neq}$

范围 (A’) ⟶ 不兼容系统 (SI)

一旦我们知道了鲁什-弗罗贝尼乌斯定理的内容，我们就会看到如何解决鲁什-弗罗贝尼乌斯定理的练习。这里有 3 个例子：使用每种方程组的定理求解的练习。

确定的兼容系统示例（SCD）

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

系统的矩阵A和扩展矩阵A’为：

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

现在我们计算矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

由于矩阵具有不同于 0 的 3×3 行列式，因此矩阵 A 的秩为 3：

$\displaystyle rg(A)=3$

一旦我们知道了 A 的阶数，我们就可以计算 A’ 的阶数，它至少是 3 阶，因为我们刚刚看到它内部有一个不同于 0 的 3 阶行列式。而且，它不可能是 4 阶，因为我们无法做出任何 4 阶行列式。因此，矩阵 A’ 的秩也是 3：

$\displaystyle rg(A')=3$

因此，由于矩阵 A 的秩等于矩阵 A’ 的秩和系统的未知数 (3)，因此根据 Rouché Frobenius 定理，我们知道它是一个兼容确定系统(SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

不确定兼容系统 (ICS) 示例

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

系统的矩阵A和扩展矩阵A’为：

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

现在我们计算矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

整个矩阵A的行列式为0，所以它不是3阶的。要判断它是否是2阶的，我们必须在A中找到一个行列式不为0的子矩阵。例如，从左上角开始的子矩阵:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

由于矩阵具有不同于 0 的 2×2 行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，因此我们尝试其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

矩阵 A’ 的所有 3×3 行列式均为 0，因此矩阵 A’ 也不会是 3 阶的。然而，它内部确实有不同于 0 的 2 阶行列式。例如：

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

因此矩阵 A’ 的秩为 2 ：

$\displaystyle rg(A')=2$

矩阵 A 的范围等于矩阵 A’ 的范围，但小于系统的未知数 (3)。因此，根据Rouché-Frobenius定理，它是一个不定兼容系统（ICS）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

不兼容系统 (IS) 示例

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

系统的矩阵A和扩展矩阵A’为：

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

现在我们计算矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

整个矩阵A的行列式为0，所以它不是3阶的。要判断它是否是2阶的，我们必须在A中找到一个行列式不为0的子矩阵。例如，从左上角开始的子矩阵:

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

由于该矩阵具有不同于 0 的 2 阶行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，所以现在我们尝试使用最后 3 列的行列式：

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

另一方面，矩阵 A’ 确实包含一个结果不为 0 的行列式，因此矩阵 A’ 的秩为 3 ：

$\displaystyle rg(A')=3$

因此，由于矩阵 A 的秩小于矩阵 A’ 的秩，我们从 Rouché-Frobenius 定理推断它是一个不相容系统(SI) ：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

解决了鲁什-弗罗贝尼乌斯定理的问题

练习1

使用 Rouché-Frobenius 定理确定以下具有 3 个未知数的方程组的类型：

查看解决方案

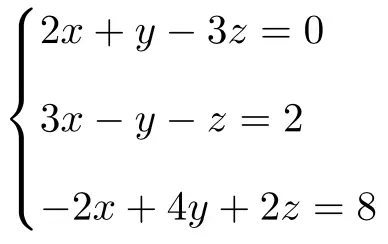
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

我们现在必须找到矩阵 A 的秩。为此，我们检查矩阵的行列式是否不同于 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

具有不同于 0 的三阶行列式的矩阵，矩阵 A 的秩为 3：

$\displaystyle rg(A)=3$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。这至少是 3 阶的，因为我们刚刚看到它内部有一个不同于 0 的 3 阶行列式。此外，它不能是 4 阶的，因为我们不能生成 4×4 的行列式。因此，矩阵 A’ 的秩也是 3：

$\displaystyle rg(A')=3$

因此，由于 Rouché-Frobenius 定理，我们知道它是一个确定兼容系统（SCD），因为 A 的范围等于 A’ 的范围和未知数的数量。

练习2

使用 Rouché-Frobenius 定理对以下具有 3 个未知数的方程组进行分类：

查看解决方案

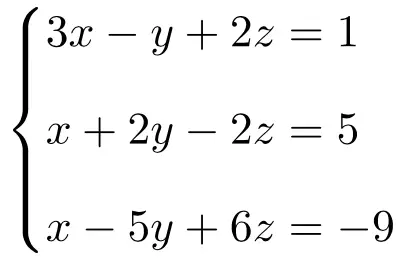
我们首先构造系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

现在我们来计算矩阵A的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，因此我们尝试其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

矩阵 A’ 的所有 3×3 行列式均为 0，因此矩阵 A’ 也不会是 3 阶的。然而，它的内部有许多不同于0的2阶行列式。例如：

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

因此矩阵 A’ 的秩为 2 ：

$\displaystyle rg(A')=2$

矩阵 A 的秩等于矩阵 A’ 的秩，但这两者都小于系统的未知数数 (3)。因此，由Rouché-Frobenius定理我们知道它是一个不定相容系统（ICS）：

练习3

使用 Rouché-Frobenius 定理确定以下方程组的系统类型：

查看解决方案

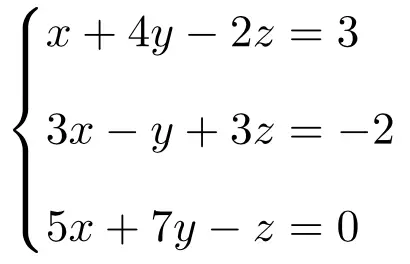
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

现在我们来计算矩阵A的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，但后 3 列的行列式则不然：

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

因此，矩阵 A’ 的秩为 3 ：

$\displaystyle rg(A')=3$

矩阵 A 的秩小于矩阵 A’ 的秩，因此我们可以从 Rouché-Frobenius 定理推断出它是一个不相容系统(SI) ：

练习4

使用 Rouché-Frobenius 定理确定以下具有 3 个未知数的方程组的类型：

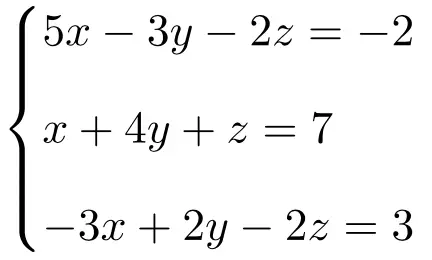
Rouche - Frobenius 定理用 3 个未知数和 3 个方程求解练习

查看解决方案

我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

现在我们必须计算矩阵 A 的秩。为此，我们使用 Sarrus 规则求解矩阵的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

具有不同于 0 的三阶行列式的矩阵，矩阵 A 的秩为 3：

$\displaystyle rg(A)=3$

因此，矩阵 A’ 的秩也是 3 ，因为它始终至少是 A 秩，并且它不能是 4 秩，因为我们无法解析任何 4×4 行列式。

$\displaystyle rg(A')=3$

因此，由于 Rouché-Frobenius 定理的应用，我们知道该系统是兼容确定系统（SCD），因为 A 的范围等于 A’ 的范围和未知数的数量。

练习5

使用 Rouché-Frobenius 定理确定以下方程组的系统类型：

查看解决方案

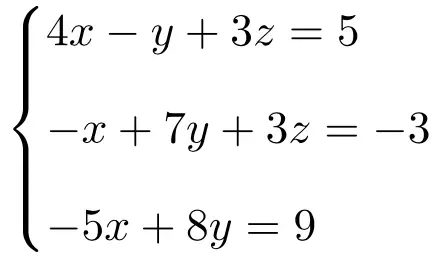
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

现在我们来计算矩阵A的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已知的前 3 列的行列式给出 0，但后 3 列的行列式没有给出：

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

因此，矩阵 A’ 的秩为 3 ：

$\displaystyle rg(A')=3$

最后，我们将域应用到 Rouché-Frobenius 定理：矩阵 A 的域小于矩阵 A’ 的域，因此它是一个不相容系统(SI) ：

练习6

使用 Rouché-Frobenius 定理对以下 3 阶方程组进行分类：

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

查看解决方案

我们首先构造系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

现在我们来计算矩阵A的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，因此我们尝试其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

矩阵 A’ 的所有 3×3 行列式均为 0，因此矩阵 A’ 也不会是 3 阶的。然而，它内部确实有不同于 0 的 2 阶行列式。例如：

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

因此矩阵 A’ 的秩为 2 ：

$\displaystyle rg(A')=2$

最后，通过应用Rouché-Frobenius定理，我们知道它是一个不定相容系统（ICS），因为矩阵A的范围等于矩阵A’的范围，但这两者都小于矩阵中未知数的数量。系统(3)：

鲁什-弗雷贝尼乌斯定理

什么是鲁什-弗罗贝尼乌斯定理？

鲁什-弗罗贝尼乌斯定理的陈述

确定的兼容系统示例（SCD）

不确定兼容系统 (ICS) 示例

不兼容系统 (IS) 示例

解决了鲁什-弗罗贝尼乌斯定理的问题

练习1

练习2

练习3

练习4

练习5

练习6

发表评论取消回复

什么是鲁什-弗罗贝尼乌斯定理？

鲁什-弗罗贝尼乌斯定理的陈述

确定的兼容系统示例（SCD）

不确定兼容系统 (ICS) 示例

不兼容系统 (IS) 示例

解决了鲁什-弗罗贝尼乌斯定理的问题

练习1

练习2

练习3

练习4

练习5

练习6

发表评论 取消回复

发表评论取消回复