平面向量方程

在此页面上您将找到平面矢量方程（公式）和计算示例。此外，您还可以通过练习来练习并解决平面矢量方程的问题。

平面的矢量方程是什么？

在解析几何中，平面的矢量方程是允许任何平面以数学方式表达的方程。要找到平面的向量方程，我们只需要一个点和属于该平面的两个线性无关向量。

平面矢量方程的公式

考虑平面的一个点和两个方向向量：

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

平面矢量方程的公式为：

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

金子

$\lambda$

和

$\mu$

是两个标量，也就是说两个实数。

因此，这意味着平面上的任何点都可以表示为 1 个点和 2 个向量的线性组合。

进一步地，上式对应一个平面的必要条件是该平面的两个向量具有线性独立性，即两个向量不能互相平行。其他。

另一方面，请记住，除了矢量方程之外，还有其他方法可以解析地表达平面，例如平面的参数方程和平面的隐式方程。您可以在链接中检查每种类型的方程是什么。

如何求平面矢量方程的示例

看完了平面矢量方程概念的解释，我们通过一个例子来看看它是如何计算的：

求通过该点的平面的矢量方程
$P(2,0,4)$

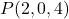
并包含向量

$\vv{\text{u}}=(1,3,-2)$

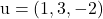
和

$\vv{\text{v}}=(5,0,1).$

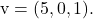
要确定平面的矢量方程，只需应用其公式：

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

现在我们将点和每个向量代入方程：

$\bm{(x,y,z)=(2,0,4)+\lambda (1,3,-2) + \mu (5,0,1)}$

正如您在示例中所看到的，找到平面的矢量方程相对容易。然而，问题可能会变得有点复杂，所以下面有几个不同难度的已解决练习，以便您练习。

平面向量方程求解问题

练习1

确定包含向量的平面的向量方程

$\vv{\text{u}}=(0,-2,3)$

并经过以下两点：

$A(1,3,-1)$

和

$B(2,-1,5).$

查看解决方案

要知道平面的方程，您需要一个点和两个向量，在这种情况下我们只有一个向量，因此我们必须找到该平面的另一个定向向量。为此，我们可以计算定义平面两点的向量：

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

现在我们已经知道了平面和点的两个方向向量，因此我们使用平面向量方程的公式：

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

我们将这两个向量和平面上的两点之一代入方程：

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

练习2

求包含以下三点的平面的矢量方程：

$A(2,-2,1) \qquad B(1,0,4) \qquad C(-1,3,-2)$

查看解决方案

为了找到平面的向量方程，我们需要找到两个在平面上结合的线性无关向量。为此，我们可以计算由 3 个点定义的两个向量：

$\vv{AB} = B - A = (1,0,4) - (2,-2,1) = (-1,2,3)$

$\vv{AC} = C - A = (-1,3,-2) - (2,-2,1) = (-3,5,-3)$

找到的两个向量的坐标不成比例，因此它们彼此线性无关。

现在我们已经知道两个方向向量和平面上的一个点，因此我们应用平面向量方程的公式：

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

我们将这两个向量和平面上的三个点之一代入方程：

$\bm{(x,y,z)=(2,-2,1)+\lambda (-1,2,3) + \mu (-3,5,-3)}$

练习3

计算空间中属于由以下向量方程定义的平面的 4 个点：

$(x,y,z)=(0,2,1)+\lambda (2,-1,4) + \mu (-1,3,0)$

查看解决方案

要计算平面上的点，只需为参数指定任意值即可

$\lambda$

和

$\mu .$

然而：

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(0,2,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(2,1,5)}$

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(-1,5,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(1,4,5)}$

练习4

求包含直线的平面的矢量方程

$r$

并且与右边平行

$s.$

是行：

$\displaystyle r: \ \begin{cases} x=4+2t \\[1.7ex] y=-1+t\\[1.7ex] z=5-4t \end{cases} \qquad \qquad s: \ \frac{x-1}{2} = \frac{y+2}{4}= \frac{z+1}{-3}$