在此页面上,您将找到关于平面是什么、平面的计算方式及其所有属性的说明。此外,您将能够看到平面的示例、两个平面之间的相对位置是什么、如何确定两个平面之间的角度,以及最后如何使用平面方程以数字方式表达任何平面。
什么是计划?
在解析几何中,平面的定义如下:
平面是具有两个维度(长度和宽度)的几何对象。
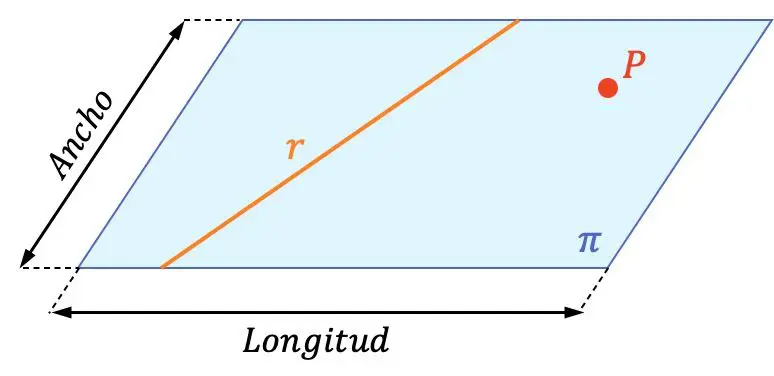
因此,平面包含无限多条线和无限多点。在上面的图形表示中,您可以看到平面、直线和点之间的区别。您还可以验证该行
![]()
和小费
![]()
包含在飞机内
![]()
正如您在图表计划中看到的,计划通常以希腊字母命名:
![]()
我们在数学中经常使用的平面的一个例子是笛卡尔平面。笛卡尔平面是由横坐标轴(X轴)和纵坐标轴(Y轴)定义的平面。笛卡尔平面的用途之一是它用于描述参考系中对象的位置。
确定计划
现在我们已经了解了平面的含义,让我们看看如何确定三维空间(R3 中)中的任意平面。
计划完全由以下几何元素决定:
- 三点未对齐。
- 一条直线和一个点在外面。
- 两条平行线或两条相交线。
关于最后一点,您可能已经知道两条线平行意味着什么。但割线的含义却鲜为人知,所以如果您在这里有任何疑问,可以查看什么是割线。
因此,如果我们具备了前面3个条件中的任何一个,就说明我们可以制定计划了。
计划财产
该计划满足以下特点:
- 一个平面包含无数个点。
- 一个平面包含无数条直线。
- 平面是无限的,也就是说,它是在空间中无限延伸的表面。
- 两个相交的平面确定一条线。
- 在平面上有一点的线不一定包含在平面上。要使一条线成为平面的一部分,它必须在平面上至少有两个点。
- 无限个平面与直线相交。
- 半平面是平面被其中一条线切割时分成的两个部分中的每一个。
平面方程
在解析几何中,平面方程是允许任何平面以数学方式表达的方程。因此,要找到平面的方程,您只需要一个点和属于该平面的两个线性无关向量。

然而,正如我们在上面对计划概念的解释中所看到的,确定计划的方法有多种。那么,同样地,分析性地表达计划也有不同的方式。
因此,所有类型的平面方程为:矢量方程、参数方程、隐式(或一般)方程和平面的正则(或分段)方程。
然后我们将详细看到该计划所有方程的解释和公式。
平面的向量方程
考虑平面的一个点和两个方向向量:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面矢量方程的公式为:
![]()
或同等学历:
![]()
金子
![]()
和
![]()
是两个标量,也就是说两个实数。
平面参数方程
平面参数方程的公式为:
![]()
金子:
-
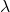
和
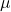
是两个标量,也就是说两个实数。
-
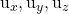
是计划的两个引导向量之一的分量
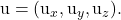
-
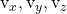
是计划的另一个定向向量的组成部分
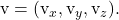
平面的隐式或一般方程
考虑平面的一个点和两个方向向量:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面的隐式、一般或笛卡尔方程通过求解以下行列式并将结果设置为 0 来获得:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
因此,所得计划的隐式或一般方程如下:
![]()
此类平面方程也称为笛卡尔平面方程。
平面的正则方程或分段方程
平面的正则或分段方程的公式如下:
![]()
金子:
-

是平面与 X 轴的交点。
-

是平面与 Y 轴的交点。
-

这是平面与 Z 轴相交的位置。
平面的正则方程(或分段方程)也可以由其一般方程得到:
![]()
首先,我们从方程中求解系数 D:
![]()
然后我们将计划的整个方程除以参数 D 改变符号的值:
![]()
![]()
并且,利用分数的性质,我们得到以下表达式:
![]()
因此,我们从这个表达式推导出允许直接计算平面的正则或分段方程的项的公式:
![]()
因此,为了能够形成该计划方程的变体,系数 A、B 和 C 必须不为零,从而避免分数的不确定性。
两个平面的相对位置
在解析几何中,两个平面之间只有三种可能的相对位置:割平面、平行平面和重合平面。
- 相交平面:如果两个平面仅相交于一条直线,则两个平面相交。
- 平行平面:如果两个平面在任何一点都不相交,则它们平行。
- 重合平面:如果两个平面都有公共点,则两个平面重合。
相交平面

平行平面

重合平面

另外,如果两个相交平面以 90° 角相交,则它们是两个相互垂直的平面。
两个平面之间的角度
两个平面之间的角度等于所述平面的法向量形成的角度。因此,为了找到两个平面之间的角度,需要计算它们的法向量形成的角度,因为它们是相等的。
因此,一旦我们确切地知道了两个平面之间的角度由什么组成,我们就可以看看计算空间中两个平面之间的角度的公式,该公式是从两个向量之间的角度公式推导出来的:
给定两个不同平面的一般(或隐式)方程:
![]()
![]()
每个平面的法向量为:
![]()
![]()
这两个平面形成的角度是通过使用以下公式计算它们的法向量形成的角度来确定的:
![]()
显然,一旦我们根据公式计算出了两个平面所成角度的余弦,就必须将余弦反转才能找到该角度的值。
另一方面,当两个平面垂直或平行时,则不必应用该公式,因为可以直接确定两个平面之间的角度:
- 两个平行平面之间的角度为 0°,因为它们的法向量具有相同的方向。
- 两个垂直平面之间的角度为 90°,因为它们的法向量也彼此垂直(或正交),因此形成直角。