在此页面上,您将找到平行四边形规则(或定律)的解释。此外,您还将看到几个使用平行四边形规则进行向量加法和减法的示例,以及实际应用。
什么是平行四边形规则?
正如您所知,向量不能像实数一样进行加减运算,因为它们有 2 个分量(在 R2 中)或 3 个分量(在 R3 中),而且向量可以有不同的方向。因此,需要其他方法来进行向量运算,例如平行四边形规则,其组成如下:
在数学中,平行四边形规则是从图形表示中添加或减去两个向量的过程。
平行四边形方法无疑是向量加法和减法(图形上)中最常用的方法,因为它是一种非常容易使用的技术。例如,在物理学中,它用于添加和减去力。
另一方面,根据我们是否要添加或减去向量,规则会略有不同,因此下面我们将分别解释这两个版本。
两个向量相加的平行四边形规则
如果我们想以图形方式将两个向量相加,应用平行四边形规则或定律的步骤是:
- 首先,我们绘制向量并将它们放置在同一应用点,也就是说,我们将两个向量的原点放在同一点。
- 然后我们在一个向量的末端画一条与另一个向量平行的线。我们用另一个向量重复该步骤。因此,我们将得到平行四边形的图(该规则的名称由此而来)。
- 最后,求和所得的向量将是平行四边形的对角线,该对角线从向量的公共原点到两条平行线的交点。
在下面的通用示例中,您可以看到如何使用平行四边形规则:

如果您想练习平行四边形规则,在以下链接中您可以查阅更多示例和几个 已求解的向量加法练习。在此页面上,您还可以找到以图形方式添加向量的其他方法,甚至如何以数字方式添加它们。
两个向量相减的平行四边形规则
平行四边形规则或方法也用于从图中减去两个向量。因此,矢量减法的步骤是:
- 首先,我们在图上表示两个向量,并将它们放置在同一应用点,也就是说,我们将两个向量的原点放在同一点。
- 其次,我们画出运算中被减的向量的相反向量,或者换句话说,我们反转正在减的向量。
- 然后我们在向量末尾画一条与符号变化向量平行的线,其总和为 。我们用另一个向量重复这个过程。这样我们就可以得到平行四边形的图形(该规则的名称由此而来)。
- 最后,减法的结果将是从两个向量的共同原点到两条平行线相交点的向量。
看下面的一般示例,其中两个向量按照平行四边形定律相减:
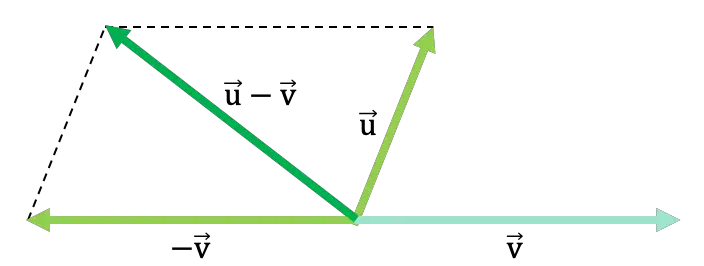
在下面的链接中,您可以看到更多使用平行四边形规则进行矢量减法的示例,您还可以通过已解决的矢量减法练习进行练习。此外,您还将找到从图形中减去向量的其他技术,以及最后如何以数字方式减去它们。
最后,如果这项技术的解释对您有用,您肯定也会有兴趣了解什么是右手定则。在链接页面上,您可以看到它是什么、它用于什么向量运算以及该规则存在的不同变体。