▷ 平均和瞬时变化率（已解决的练习）

这里我们解释什么是变化率、平均变化率和瞬时变化率。您将能够看到几个有关如何计算变化率的示例，此外，您将能够通过已解决的变化率分步练习进行练习。

变化率是多少？

在数学中，函数的变化率（TV）是函数在两个不同点处的值之差。因此，要计算两点之间的变化率，必须将这两点处的函数值相减。

$\text{TV}[a,b]=f(b)-f(a)$

例如，如果函数的两个图像分别为 f(2)=1 和 f(5)=7，则它们的变化率为：

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

我们刚刚看到了变化率的数学含义，但在经济学中，变化率的概念含义如下：

在经济学中，两个数值之间的变化率是用百分比表示的它们之间的差值，即一个变量在不同时期之间的变化率就是它的相对变化。因此，要计算变化率，需要将两个不同周期的值相减，并将得到的结果除以初始周期的值。

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

例如，如果某些股票的价值在一个月内从 35 欧元增加到 50 欧元，则其变动率为：

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

考虑到变化率的两种可能含义，在本文中我们将重点了解变化率的数学定义。可以区分两种类型的变化率：平均变化率和瞬时变化率。下面是每种类型的解释。

平均变化率

函数在某个区间内的平均变化率 (TVM) 是指函数自变量每增加一个单位而增加（或减少）的单位数。因此，函数的平均变化率是通过将函数在某个区间内的增长除以该同一区间的幅度来计算的。

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

为了让您了解平均变化率是如何计算的，我们在下面逐步解决了一个示例。

计算函数平均变化率的示例

计算以下函数在区间[2.5]内的平均变化率：

$f(x) = x^2-1$

首先，我们计算函数在 x=2 和 x=5 处的值：

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

然后我们简单地应用以下公式计算函数在区间内的平均变化率：

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

由于TVM[2,5]的结果为正，这意味着函数在区间[2,5]内增长。另一方面，如果结果为负，则意味着函数在此区间内下降。

平均变化率的几何解释

在几何上，函数在区间内的平均变化率表示连接区间极值点的直线的斜率。

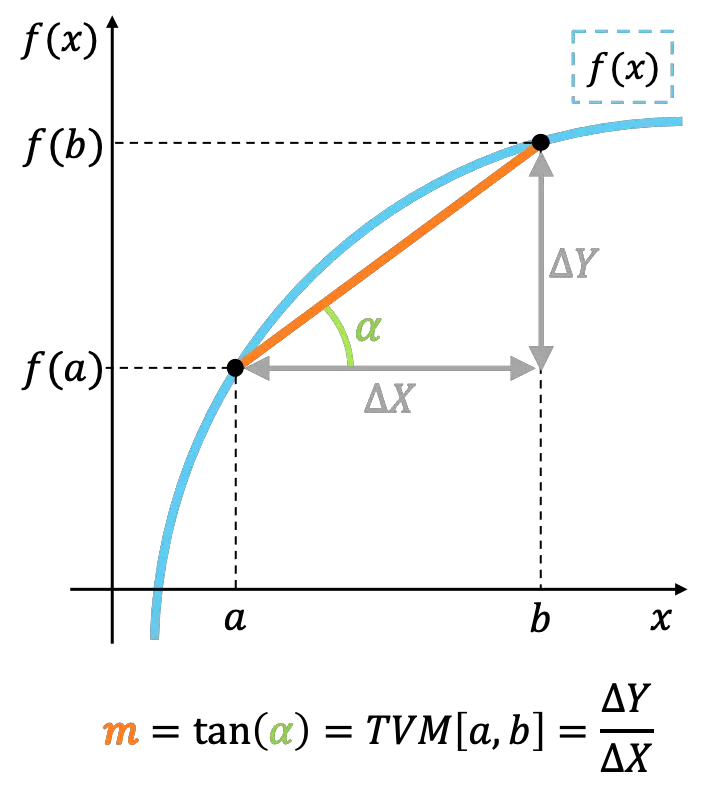
瞬时变化率

函数在某一点的瞬时变化率 (TVI) 是函数在一段时间内相对增加的无穷小极限。因此，通过使h趋于零来求解f(a+h)-f(a)的商的极限来计算瞬时变化率。

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

瞬时变化率的值可以是正数、负数或零，表示该点的函数在该点分别是增加、减少或保持不变。

计算函数瞬时变化率的示例

计算以下函数在 x=2 点处的瞬时变化率：

$f(x) = x^2$

为了计算瞬时变化率，我们需要应用以下公式：

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

我们解析显着的身份：

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤如果您不再记得重要恒等式的公式，您可以在我们专门研究多项式的网站上找到所有公式： www.polinomios.org

现在让我们尝试解决这个极限：

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

但我们发现零之间的不确定性为零，因此：

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤请参阅： 如何求解零之间具有零不确定性的极限

最后我们解决极限：

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

然而：

$\mathbf{TVI} \bm{(2) = 4}$

由于 TVI(2) 的结果为正，这意味着函数在 x=2 时增加。另一方面，如果结果为负，则意味着该函数在此阶段正在下降。

瞬时变化率的几何解释

从几何角度来看，函数在某一点的瞬时变化率表示该函数在该点的切线的斜率。

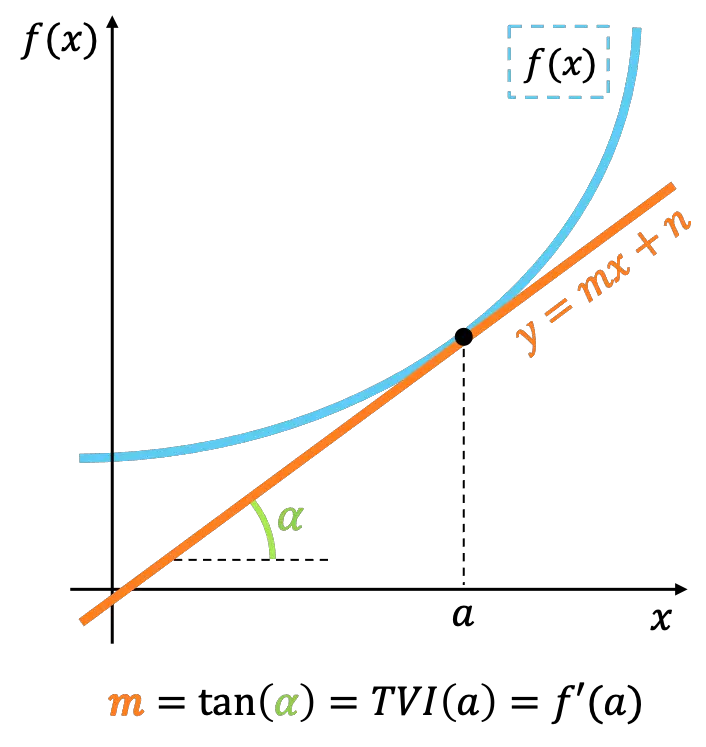
如果仔细看的话，瞬时变化率的含义就相当于函数导数的概念。因此，瞬时变化率也用于计算函数在某一点的导数值。

已解决变化率练习

练习1

计算下列函数在区间[1,3]内的变化率值。

$f(x)=x^2-5$

查看解决方案

首先，我们确定函数在区间末端的值：

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

现在我们应用变化率公式：

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

练习2

计算以下函数在区间 [1,4] 内的平均变化率 (TVM)：

$f(x)=2x+1$

查看解决方案

我们首先计算函数在 x=1 和 x=4 处的图像。

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

我们应用平均变化率的公式：

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

练习3

求下列函数在区间[-1.3]内的平均变化率：

$f(x)=(x+1)^2$

查看解决方案

为了确定平均变化率，我们首先需要计算 f(-1) 和 f(3)：

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

我们现在使用平均变化率的公式：

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

练习4

计算下图所示函数在区间[2,4]内的平均变化率：

查看解决方案

我们应用平均变化率的公式：

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

正如我们在公式中看到的，我们需要找到 f(4) 和 f(2) 的值。通过查看函数的图形表示可以轻松完成此操作：

$f(4)=5$

$f(2)=1$

现在我们知道了函数的值，我们将它们代入公式：

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

练习5

计算下列函数在 x=2 点处的瞬时变化率：

$f(x)=3x$

查看解决方案

为了确定函数在 x=2 点处的瞬时变化率，我们应用相应的公式：

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

练习6

确定以下函数在 x=1 点处的瞬时变化率 (TVI)：

$f(x)=x^2+1$

查看解决方案

我们应用瞬时变化率的公式：

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

然后，我们计算

$f(1+h)$

和

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

我们将在极限中找到的值替换为：

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

我们解决了著名的产品：

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

现在让我们尝试解决这个极限：

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

但是我们发现零除以零的不定形式，因此我们对分数分子的多项式进行因式分解并化简：

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤如果您不知道如何求解零之间的零不确定性，您可以在上面的链接中查看有关如何求解零之间的零不确定性极限的完整说明。

最后，我们解决了限制：

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

综上所述，函数在x=1点处的瞬时变化率等于2。

$\mathbf{TVI} \bm{(1) = 2}$

练习7

求下列函数在 x=2 点处的瞬时变化率：

$f(x)=4x^2-x+3$

查看解决方案

我们首先使用瞬时变化率公式：

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

我们计算

$f(2+h)$

和

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

我们将在极限中找到的值替换为：

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

我们计算显着的等式：

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

我们对分子进行运算：

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

现在让我们尝试解决这个极限：

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

但我们得到的不确定性为零除以零，因此我们对多项式进行因式分解并简化：

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

最后，我们解决了限制：

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

然而：

$\mathbf{TVI} \bm{(2) = 15}$

变化率是多少？

平均变化率

计算函数平均变化率的示例

平均变化率的几何解释

瞬时变化率

计算函数瞬时变化率的示例

瞬时变化率的几何解释

已解决变化率练习

练习1

练习2

练习3

练习4

练习5

练习6

练习7

发表评论 取消回复

发表评论取消回复