在此页面上,您将找到对齐点的解释。您还将看到可用于确定 3 个(或更多)点是否对齐的所有方法。此外,您还会找到一些示例,甚至已解决的练习,以便您进行练习。
点对齐是什么意思?
在解析几何中,如果三个或更多点都在同一条线上,也就是说,如果可以通过在它们之间画一条直线将它们连接起来,则它们是对齐的。
显然,两个点总是对齐的,因为您总是可以在两点之间画一条线。然而,三个点不必在同一条线上。主要有两种方法可以知道3个或更多点是否对齐:
- 矢量方法:包括查看形成点的矢量是否成比例。
- 线方程法:判断点是否属于同一条直线。
以下是每个过程和示例的说明,以便您可以决定哪一个最适合您。
如何用向量方法判断3个(或更多)点是否对齐
考虑三点:
![]()
如果向量则这三个点对齐
![]()
和
![]()
它们具有相同的方向,也就是说它们的分量是否成比例。
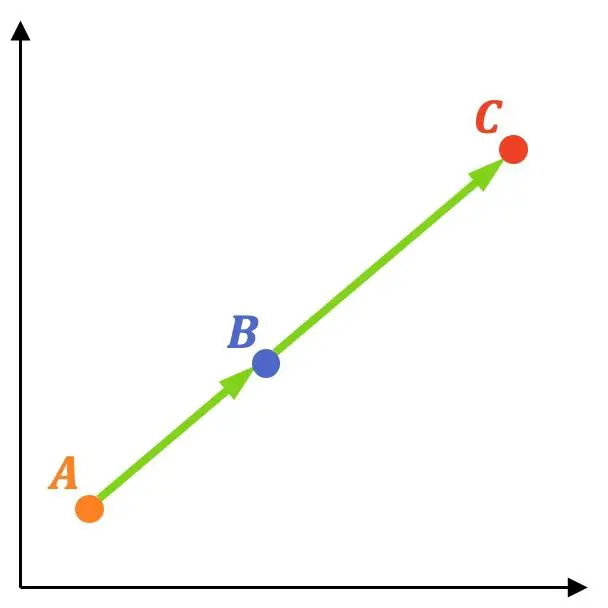
让我们看一个如何完成此操作的示例:
- 判断以下3点是否对齐:
![]()
首先,我们计算点之间的向量。计算两个不同的向量就足够了:
![]()
![]()
然后我们检查向量的坐标是否成比例:
![]()
通过将两个向量的 X 分量和 Y 分量相除,我们得到相同的结果 (-2),因此向量具有相同的方向,因此点是对齐的。
此方法还可用于找出三个或更多点在空间中是否对齐(在 R3 中),唯一需要添加的是检查两个向量的第三个分量(Z 分量)是否也成比例。
如果本文对您有用,您可能还会有兴趣了解如何计算两点之间的中点,因为显然,找到 2 点的中点是确定与其他两点对齐的第三点的一种方法。您可以在链接页面上看到它是如何完成的,此外您还可以看到逐步解决的示例和练习。
如何用直线方程法判断3个(或更多)点是否对齐
正如我们在上一节中看到的,研究 3 个或更多点对齐的一种方法是使用它们之间形成的向量。那么,另一种方法是从直线方程开始:
考虑三点:
![]()
如果这三个点都属于同一直线,则这三个点对齐。因此,要知道三个或更多点是否对齐,必须遵循以下步骤:
- 求通过这三个点中的两个点的直线方程。
- 检查第三个点是否也属于该直线。在这种情况下,这意味着 3 个点对齐,但是如果不满足条件,则意味着这些点未对齐。
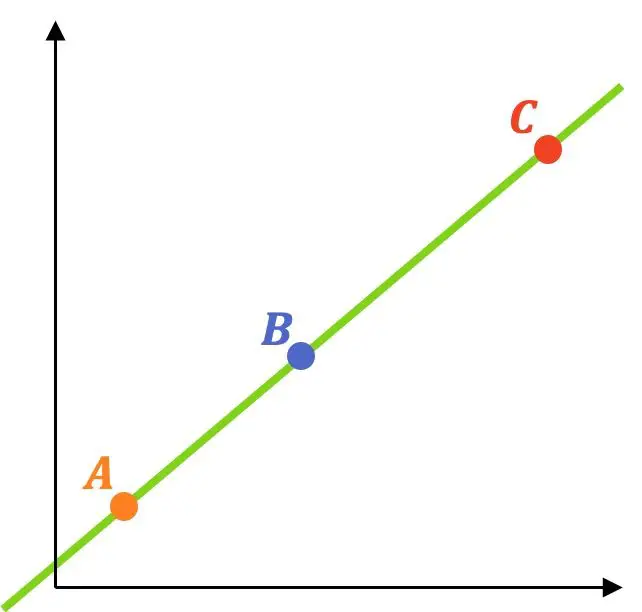
例如,我们将使用此方法解决一个练习:
- 检查以下 3 点是否对齐:
![]()
首先,我们必须计算经过A点和B点的直线方程。因此我们求出直线的方向向量:
![]()
现在你必须构造直线方程,你可以选择你想要的类型:参数、隐式、一般等。但在这种情况下,我们将使用连续方程。那么经过A点和B点的直线的连续方程为:
![]()
一旦我们有了直线方程,我们必须检查另一个点是否也属于同一条直线。为此,我们将 C 点的坐标代入直线方程:
![]()
![]()
![]()
我们得到了平局,所以该点满足直线方程。因此这 3 个点共线。
需要注意的是,一组对齐点不必是等距的,即几个对齐点之间的距离可以不同。您可以在两点(几何)之间的距离的解释中看到这两个概念之间的区别,您还可以在其中看到逐步解决的示例和练习。
解决对齐点练习
练习1
判断以下3点是否对齐:
![]()
我们可以选择我们见过的两种方法中的一种来解决问题。在这种情况下,我们将使用向量方法。
首先,我们计算点之间的向量:
![]()
![]()
现在我们检查向量的笛卡尔坐标是否成比例:
![]()
通过将两个向量的 X 分量和 Y 分量相除,我们得到相同的结果 (-4),因此向量具有相同的方向。表明点对齐的事实。
练习2
给出3点:
![]()
确定哪些与以下两点相符:
![]()
在这种情况下,我们将使用直线方程方法,这样我们将节省一些计算。
因此,我们计算通过 D 点和 E 点的直线的连续方程:
![]()
![]()
现在让我们检查哪些点对应于直线方程,因此与点 D 和 E 对齐,哪些点不对齐。
我们检查A点:
![]()
![]()
![]()
直线方程不成立,因此A 点未与 D 点和 E 点对齐。
我们现在检查B点:
![]()
![]()
![]()
在这种情况下,满足直线方程,因此B 点与 D 点和 E 点共线。
最后,我们在 C 点重复这个过程:
![]()
![]()
![]()
直线方程不成立,因此C 点未与 D 点和 E 点对齐。
练习3
寻找未知的价值
![]()
以便以下 3 点对齐:
![]()
在这种情况下,我们将使用向量方法。
因此,我们尝试计算点之间的向量:
![]()
![]()
为了满足三点共线性,两个向量的坐标必须成比例。因此我们应用这个条件:
![]()
我们求解方程:
![]()
![]()
![]()
![]()
![]()
![]()
这样3个点就对齐了
![]()
必须值 2。