在此页面上,您将找到对称矩阵的解释。另外,我们还向您展示如何快速识别矩阵何时对称,并提供几个示例,让您毫无疑问。您还将发现对称矩阵的所有属性。最后,我们解释任何方阵都具有的一个特殊特征:它可以分解为对称矩阵和反对称矩阵的和。
什么是对称矩阵?
对称矩阵的定义如下:
对称矩阵是一个方阵,其转置等于矩阵本身。
![]()
金子
![]()
表示转置矩阵
![]()
。
一旦我们知道了对称矩阵的概念,我们就会看到如何轻松识别任何对称矩阵:
矩阵何时对称?
认识对称矩阵的结构非常简单:第i行j列的元素必须与第 j行i列的元素相同。并且矩阵主对角线的值可以是任意的。
对称矩阵的示例
下面举几个对称矩阵的例子来帮助你理解:
2 × 2 阶对称矩阵的示例
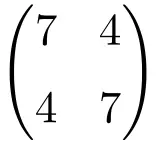
维度为 3×3 的对称矩阵的示例

大小为 4×4 的对称矩阵的示例
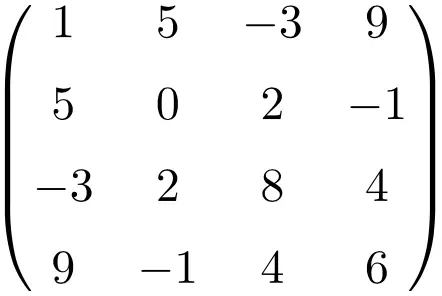
通过转置这三个矩阵,我们验证它们是对称的,因为转置矩阵相当于它们各自的原始矩阵。
为什么叫对称矩阵呢?
如果仔细观察前面的示例,对称矩阵的主对角线是对称轴,或者换句话说,它充当对角线上方数字和下方数字之间的镜子。因此,这些类型的矩阵称为对称矩阵。
对称矩阵的性质
对称矩阵的特点如下:
- 两个对称矩阵相加(或相减)得到另一个对称矩阵。由于转置两个相加(或相减)的矩阵相当于分别转置每个矩阵:
![]()
- 任何对称矩阵乘以标量也会产生另一个对称矩阵。
- 同样,两个对称矩阵之间的矩阵乘积并不总是等于另一个对称矩阵,只有当且仅当两个矩阵可以交换时。这个条件可以用转置矩阵乘法性质来证明:
![]()
- 只要指数是整数,对称矩阵的幂就会产生另一个对称矩阵。
- 显然,酉矩阵和零矩阵都是对称矩阵的例子。
- 与对称矩阵全等的矩阵也必须是对称的。
- 如果一个对称矩阵是正则或可逆的,那么它的逆矩阵也是对称的。
- 与对称矩阵的伴随相同:对称矩阵的伴随矩阵给出另一个对称矩阵作为解。
- 真正的对称矩阵也是正规矩阵。
- 由于对称矩阵是埃尔米特矩阵的特例,因此对称矩阵的所有特征值(或多个特征值)都是实数。
- 谱定理告诉我们,所有元素为实数的矩阵都是可对角化的矩阵,而且,对角化是通过正交矩阵进行的。因此,所有实对称矩阵都是正交对角化的。
- 另一方面,具有复数的对称矩阵可以通过酉矩阵进行对角化。
- Hessian 矩阵始终是对称的。
将方阵分解为对称矩阵和反对称矩阵
方阵的一个特点是它们可以分解为对称矩阵加反对称矩阵的和。
允许我们执行此操作的公式如下:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b9aa2b7ed0e9ce31587d4f00f1144e_l3.png)
其中C是我们要分解的方阵,C是其转置,最后S和A分别是矩阵C分解成的对称矩阵和反对称矩阵。
下面有一个已解决的练习,您可以了解这是如何完成的。让我们分解以下矩阵:
![Rendered by QuickLaTeX.com \displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-852a7267895a7f332ad3f28f8a8dda0d_l3.png)
我们用以下公式计算对称和反对称矩阵:
![Rendered by QuickLaTeX.com \displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-994670ecc17b3bc8757482f1656e543e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d87e1d30d2bc657c20535f45c0fb7be6_l3.png)
我们可以通过将两个矩阵相加来检查方程是否满足:
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cfdbffec6801c13041cd2996da13e96_l3.png)
![]()
✅