在本文中,我们解释什么是对称函数(偶函数和奇函数)以及如何研究函数的对称性。您还将能够看到这些类型函数的属性,最后,您将能够练习逐步解决对称函数的练习。
什么是对称函数?
对称函数是可以在其图形表示中找到对称轴的函数。对称函数有两种类型:偶函数,关于 Y 轴对称;奇函数,关于坐标原点对称。
请记住,对称轴是一条假想线,它将任何东西分成两部分,以便它们的相对点彼此等距。
偶函数
偶函数是关于 y 轴对称的函数,即 Y 轴是函数的对称轴。
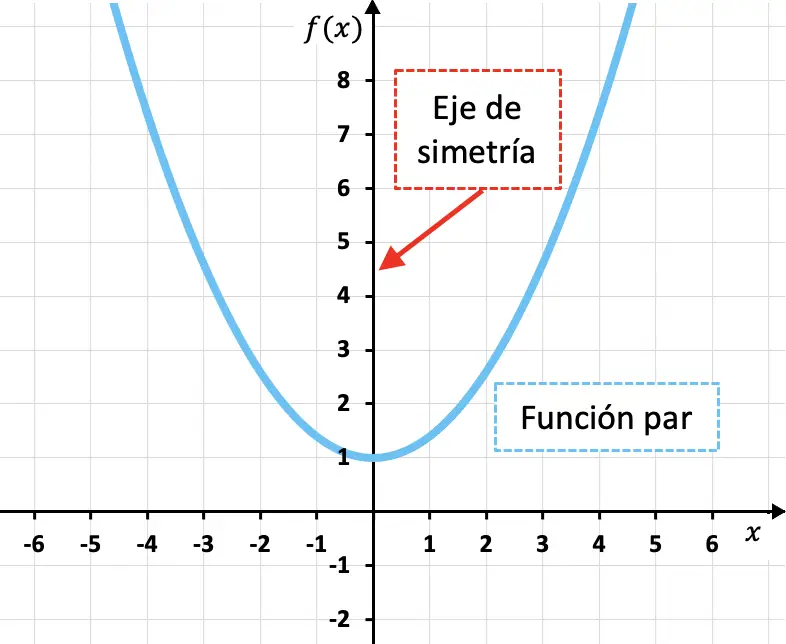
正如您在上面所示的二次函数中所看到的,偶函数对于自变量 (x) 的任何值的图像都相当于相反值 (-x) 的函数的图像。换句话说,从数学上来说,一个函数满足以下条件就是偶数:
![]()
偶函数是对称函数的一种,现在让我们看看奇函数是什么样的。
奇函数
奇函数是相对于坐标原点(即相对于点 (0,0))对称的函数。
下面你可以看到一个奇函数的图形:
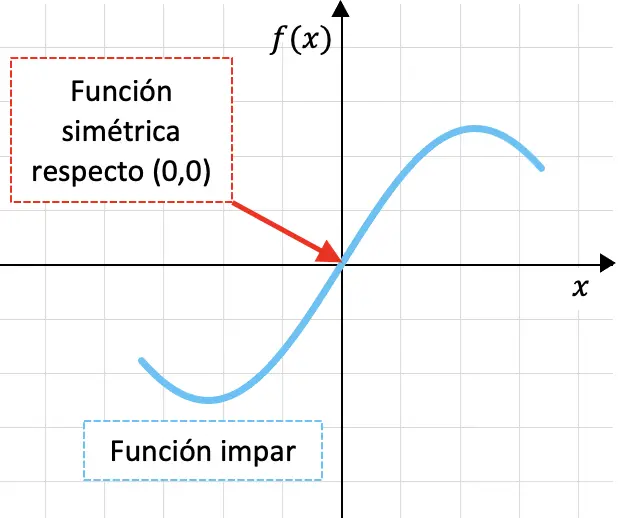
函数关于坐标原点对称的事实意味着,如果我们首先通过 OY 轴然后通过 OX 轴折叠函数的图形,则函数的图形将重叠。
从代数上来说,如果一个函数的图像之间满足以下关系,则该函数是奇函数:
![]()
了解函数的对称性对于表示它非常有用,因为只知道图形的一半,我们就可以快速绘制另一部分。
如何求函数的对称性
为了研究函数的对称性,我们必须计算
![]()
,也就是说需要计算
![]()
因此,根据图像的结果,函数的对称性将是:
- 如果已满
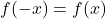
,该函数是偶函数,因此关于 Y 轴对称。
- 如果已满
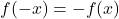
,该函数是奇数,因此相对于坐标原点对称。
- 如果以上条件都不满足,则它是非对称函数(没有对称轴)。
例如,我们来分析以下三次函数的对称性:
![]()
为了研究函数的对称性,我们计算
![]()
![]()
生成的代数表达式与原始函数表达式等效,但改变了符号,或者换句话说,满足以下等式:
![]()
因此,该函数是奇函数,因此相对于坐标原点 (0,0) 对称。
对称函数的性质
对称函数具有以下特点:
- 两个偶/奇函数的和等于另一个偶/奇函数。
- 两个偶函数或两个奇函数的乘积给出一个偶函数。
- 偶/奇函数的导数是偶/奇函数。
- 两个偶/奇函数的复合相当于一个偶/奇函数。
- 唯一既是偶数又是奇数的函数,即关于 OY 轴和原点对称的函数是
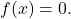
解决了函数的对称性问题
练习1
求以下函数的对称性:
![]()
为了计算函数的对称性,我们需要评估
![]()
![]()
负数的任何指数次幂都会得到正数,因此在这种情况下,以下等式成立:
![]()
因此该函数是偶函数,因此它关于 y 轴 (Y 轴) 对称。
练习2
研究以下有理函数的对称性:
![]()
为了确定函数的对称性,我们这样做
![]()
![]()
在这个问题中,不满足对称条件,因为图像
![]()
不等于
![]()
也不
![]()
![]()
因此,该函数没有对称轴,而是一个不对称函数。
练习3
计算以下函数的对称性:
![]()
为了分析函数的对称性,我们需要计算
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
在这种情况下,结果表达式与原始表达式类似,但符号发生了变化,因此满足以下等式:
![]()
因此,该函数是奇函数,因此相对于坐标原点 (0,0) 对称。