在本页中,我们将解释什么是完美平方三项式以及如何解释它。此外,您将能够看到几个示例并通过逐步完美平方三项式练习进行练习。
什么是完美平方三项式?
显然,在了解完全平方三项式的含义之前,您需要知道什么是三项式,因此我建议在继续之前查看此链接页面(其中详细解释了它)。
因此,完美平方三项式的定义如下:
在数学中,完美平方三项式也称为TCP ,是通过二项式平方得到的三项式。
因此,完全平方三项式由具有两个完全平方的多项式和另一项(即这些平方的底的二重积)组成。

从上面的两个公式可以看出,完美平方三项式是由两个显着恒等式(或显着乘积)获得的,这就是它如此重要的原因。具体来说,当求解加法的平方或减法的平方时,可以找到完美的平方三项式。
完全平方三项式示例
为了理解完全平方三项式的概念,我们将逐步解释两个例子:
实施例1
![]()
这个例子是一个完全平方三项式,因为在它的代数表达式中有两个完全平方(即,它们有一个精确的平方根),因为
![]()
和 9 相当于
![]()
和 3 分别求 2 次方:
![]()
![]()
更多的是,三项式的最后一项
![]()
它是通过将前两个平方的底数相乘并乘以 2 获得的:
![]()
因此,本练习中所有完整的显着恒等式将是:
![]()
实施例2
![]()
这个另一个例子也是完全平方三项式,因为满足了 3 个必要条件:两项对应于两个完全平方,另一项是这些平方的底相互乘以 2 的结果。
![]()
![]()
![]()
在这种情况下,完全平方三项式具有负单项式,因此它对应于平方差的显着等式的发展:
![]()
如何因式分解完美平方三项式
在代数中,一个非常常见的问题是完美平方三项式 (PCT) 的因式分解。如果您不知道这意味着什么,对多项式进行因式分解意味着将其表达式转换为因式的乘积。
因此,为了分解这种类型的代数三项式,必须遵守以下规则:
- 三项式必须有两个完全平方数,我们称之为
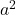
和
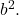
- 三项式的第三项必须等于两个完全平方的底的二重积,这在数学上对应于表达式
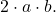
- 因式分解的三项式将是
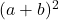
如果完全平方三项式的所有项都为正,否则,如果平方底的二乘积有负号,则因式分解的三项式将为
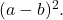
为了理解这个过程,我们将逐步解决一个练习:
- 对以下完全平方三项式进行因式分解:
![]()
我们需要做的第一件事是确定三项式是否有两个完全平方的元素,或者换句话说,它的平方根是否不给出小数。在这个问题中
![]()
是变量的平方
![]()
36 是 6 的平方:
![]()
![]()
因此三项式有两个完全平方数。
其次,我们必须检查中间项是否等于上一步计算的两个根的二重积:
![]()
这条规则也受到尊重。
那么所有的条件都满足了。因此,因式分解的完全平方三项式是由找到的两个根形成的二项式(
![]()
和数字 6) 的平方:
![]()
由于中间项是负数,我们还必须在括号中加上减号。另一方面,如果它是正数,我们就必须添加一个总和:
![]()
从逻辑上讲,因式分解是一个复杂的过程,因此,除了尝试进行下面的练习之外,我建议查看这些因式分解多项式的示例。在此链接中,我们还解释了一种方法,该方法不仅用于因式分解三项式,而且还用于因式分解任何类型的多项式,而且速度同样快。
完美平方三项式的习题解答
应用相应的公式将以下三项式转换为平方二项式:
![]()
![]()
![]()
![]()
![]()
要将完全平方三项式转换为平方二项式的幂,您必须使用和的平方和差的平方的显着恒等式的公式,它们是:
![]()
![]()
然而:
![]()
![]()
![]()
![]()
![]()
⬇⬇⬇ 不要忘记您可以在下面的评论中写下您所有的问题! ⬇⬇⬇