在此页面上，您将了解如何除多项式，包括多项式除以单项式以及多项式除以另一个多项式。您还可以看到多项式除法的示例，并通过逐步解决的练习进行练习。此外，您还会发现该多项式运算的属性。
多项式（或多项式）除法
在我们确切地了解两个多项式如何相除之前，我们将简要回顾一下多项式除法的概念，以便更容易理解我们将要使用的方法。
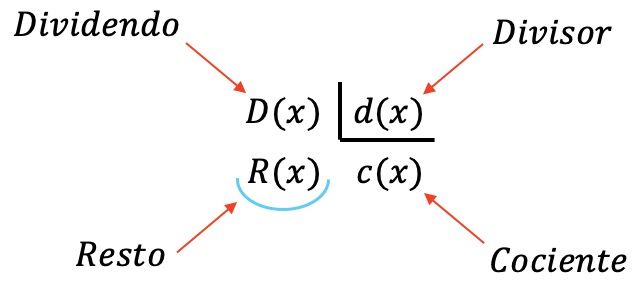
多项式除法涉及四个多项式：
- 股息：除多项式。
- 除数：除以被除数的多项式。
- 商：被除数除以除数的结果。
- 余数（或残差）：两个多项式相除时剩下的多项式。
另一方面，您还应该知道多项式之间的除法有两种类型：
- 多项式的精确除法：当余数为零时，多项式之间的除法是精确的。在这种情况下，多项式被除数等于除数乘以商。
此外，在这种情况下，股息
是除数的倍数
和商
同样，多项式除数和多项式商都是被除数的除数。
- 多项式的整数除法：在多项式的整数（或不精确）除法中，余数不为零 (0)。那么，满足多项式除法的基本性质：
现在我们已经了解了什么是除法多项式，让我们看看如何将多项式除法。更准确地说，我们将首先解释多项式和单项式之间的除法，然后解释两个多项式之间的除法。
多项式除以单项式
在了解如何将多项式除以单项式之前，我们首先回顾一下单项式是如何除以它们的，因为有必要知道它才能进行这种类型的多项式运算。
两个单项式相除涉及将它们的系数彼此相除以及它们的文字部分彼此相除，即单项式的系数相除并减去具有相同基数的变量的指数。看下面的例子：
现在让我们看看多项式除以单项式涉及什么：
在数学中，为了解决多项式除以单项式的问题，多项式的每一项都除以单项式。
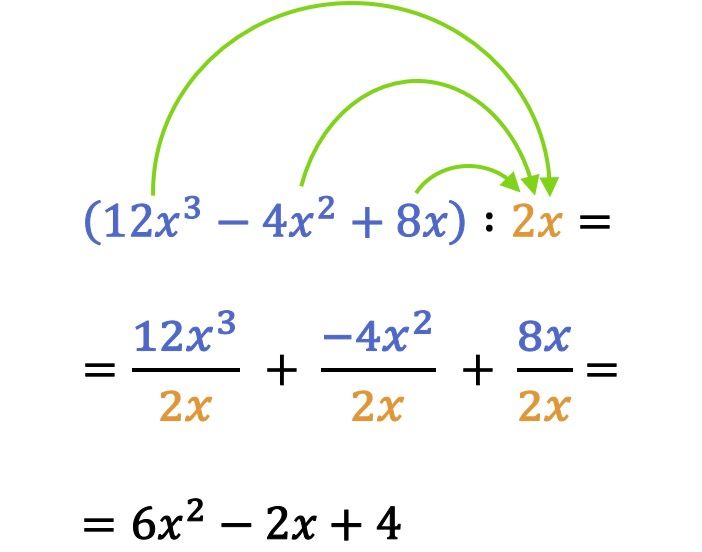
请注意，在前面的除法示例中，除单项式或多项式时，还必须考虑符号规则。事实上，多项式和单项式除法中一个非常常见的错误是弄错了项的符号。
多项式除以另一个多项式
要将两个多项式相除，您需要遵循一个过程，因此让我们通过逐步求解示例来看看多项式相除（也称为多项式长除法）的方法是什么样的：
- 计算多项式相除的结果
多项式之间
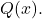
是两个多项式：
首先要做的是将多项式转化为除法形式。在左边我们写下分数的分子（被除多项式），在右边我们写下分数的分母（除数多项式）：
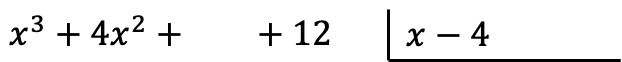
警告：如果多项式没有一定次数的单项式，我们必须在其位置留一个空格。例如，多项式
没有第一年学期，因此有一个空白。
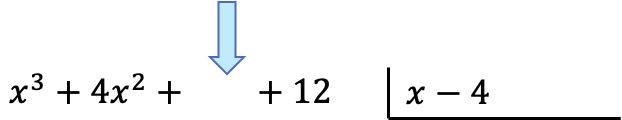
一旦我们有了多项式，我们就可以找到商。为了找到商的第一项，我们必须将被除数的第一项除以除数的第一项：
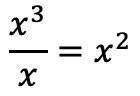
我们用除法的结果代替商：
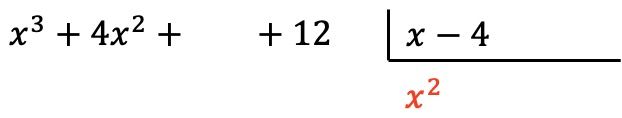
现在，我们将找到的项与除数的每个元素相乘，然后将每个结果放在相应列的被除数下方，并更改其符号：
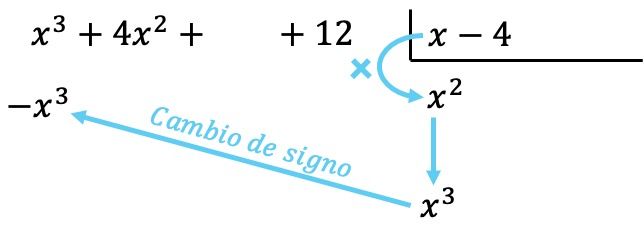
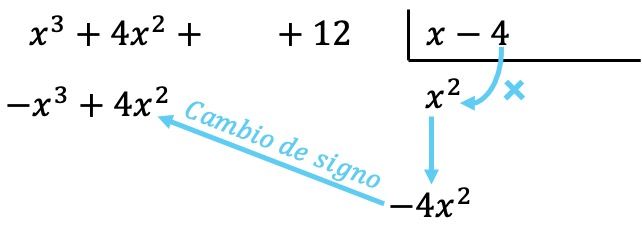
与多项式的所有运算一样，将多项式从最高次到最低次排序非常重要，以便相同次数的所有项都在同一列中。
一旦我们将乘法结果带相反的符号，我们需要添加垂直对齐的项：
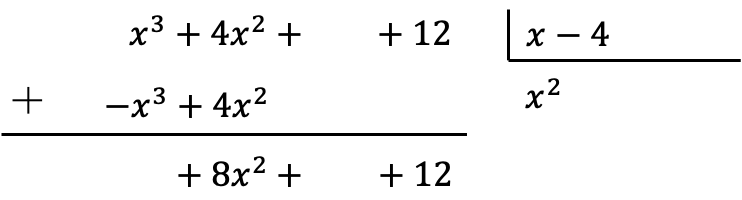
请注意，通过进行此求和，最高次数的系数会被抵消，因此，我们的红利项会少一项。
现在我们需要重复相同的过程，直到多项式被除数比多项式除数小一级。
因此，我们将股息的第一项除以除数的第一项：
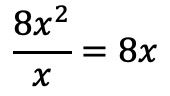
我们将结果放入商中：
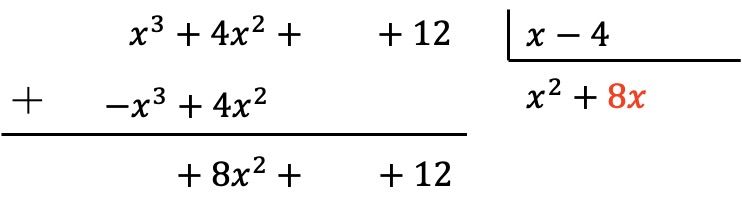
和以前一样，我们将商的新项乘以除数的每个元素，并将相反符号的结果放入被除数的相应列中：
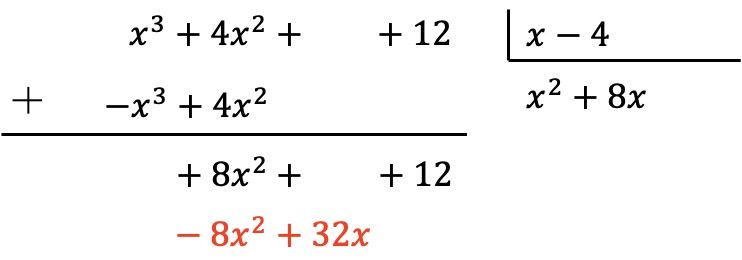
我们垂直添加：
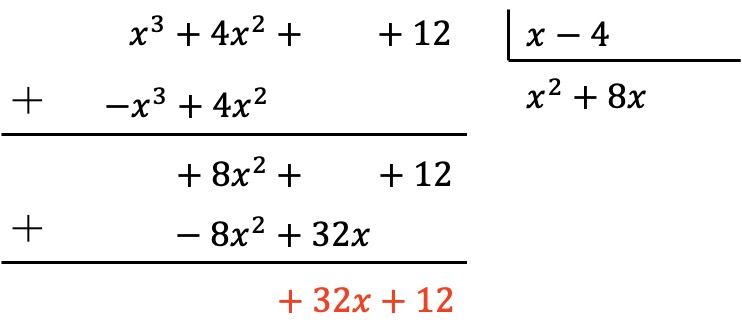
被除数多项式仍然不比除数多项式小一级，所以我们需要继续做同样的过程。
因此，首先我们将被除数的第一项除以除数的第一项，然后将结果乘以除数的每一项，然后将修改后的结果带入被除数中，最后垂直相加：
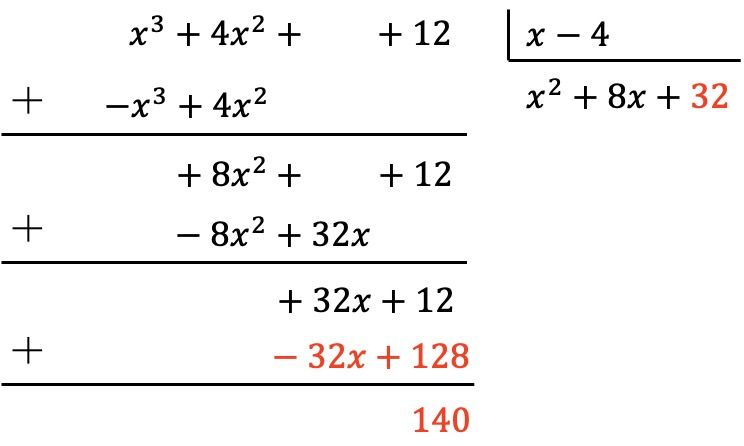
所以我们已经得到被除数的多项式的次数小于除数的次数，因为被除数的次数为0，除数的次数为1。因此，除法完成。
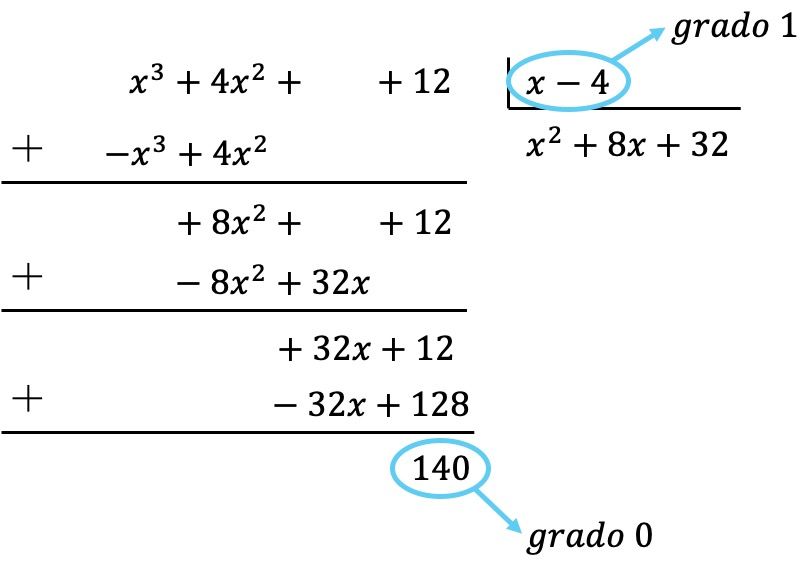
因此，除法的结果是：
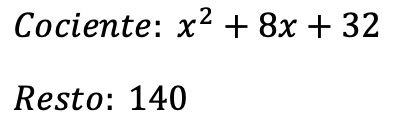
另一方面，我们可以根据多项式除法的基本条件来验证我们是否正确地执行了多项式除法：
✅
满足方程，因此多项式除法正确执行。
这样我们就完成了多项式除法，我们希望能够帮助您解释这一点。您对多项式除法的看法如何？你有疑问吗？你喜欢它？或者您希望多项式除法不存在？ 😂 我们在评论中读到了你的信息！ 👇👇👇
除法多项式的性质
任何多项式除法都满足以下特征：
✓多项式被除数的次数必须始终大于多项式除数的次数。
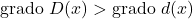✓多项式被除数的次数等于除数和商的次数之和。
✓余数的次数始终小于除数的次数（因此也小于被除数的次数）。
✓被除数等于除数乘以商的乘积加上余数。这个条件也放在数的除法中。
解决了多项式除法的练习
练习1
确定以下多项式除以单项式的结果：
要将多项式除以单项式，您必须求解多项式的每一项除以所述单项式：
![\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffa558b26adc36e2ac45a842a6cf33df_l3.png "Rendered by QuickLaTeX.com")
请记住，在单项式之间进行除法时，系数会在它们之间相除，并减去底数相同的幂的指数。
练习2
计算以下多项式除以单项式：
要将多项式除以单项式，您必须将多项式的每一项除以所述单项式：
![\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868da1546d3e4d33e8226774020cbb2d_l3.png "Rendered by QuickLaTeX.com")
请记住，在单项式除法中，系数彼此相除，并减去具有相同底数的幂的指数。
练习3
求解以下多项式除以单项式：
要将多项式除以单项式，您必须求解多项式的每一项除以所述单项式：
![\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8d5fe46b397f2f531a865e7cb0df3cf_l3.png "Rendered by QuickLaTeX.com")
请记住，除法单项式是负数，因此所有除法的符号都会改变。
练习4
对多项式执行以下除法：
要除多项式，您必须应用上面解释的方法：
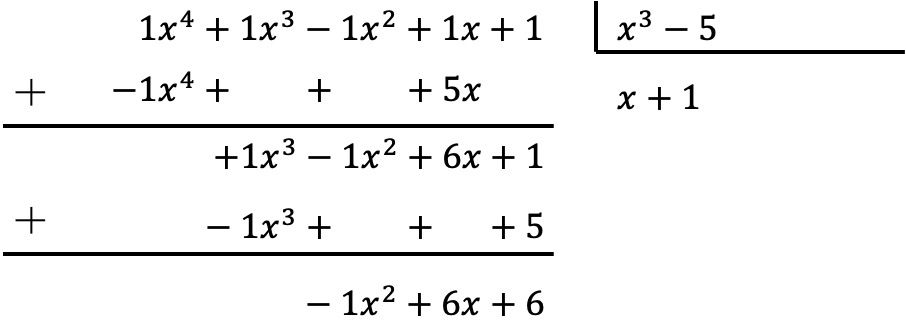
因此，两个多项式相除的结果是：
商：
休息：
练习5
计算以下多项式除法：
为了解决多项式除以二项式的问题，我们必须应用上面看到的方法：
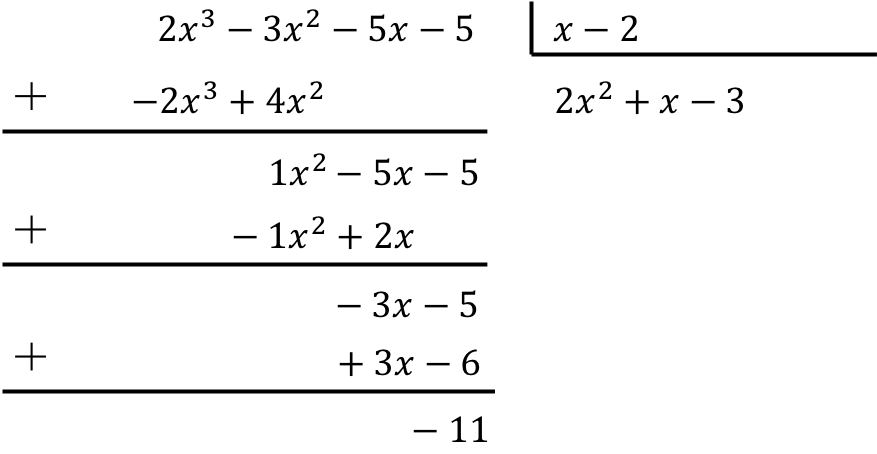
因此，多项式除法的结果是：
商：
休息：
练习6
求解以下多项式除法：
要计算多项式的除法，我们必须应用解释的方法：
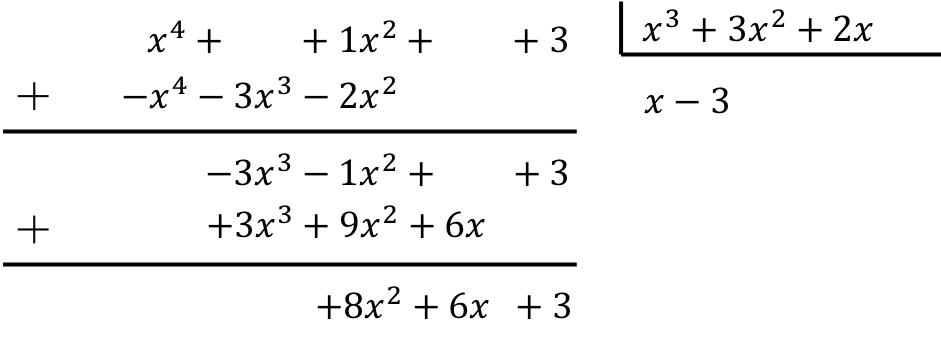
因此，两个多项式相除的结果是：
商：
休息：
练习7
求以下 2 个多项式相除的结果：
要计算多项式除以三项式，您必须应用以下方法：
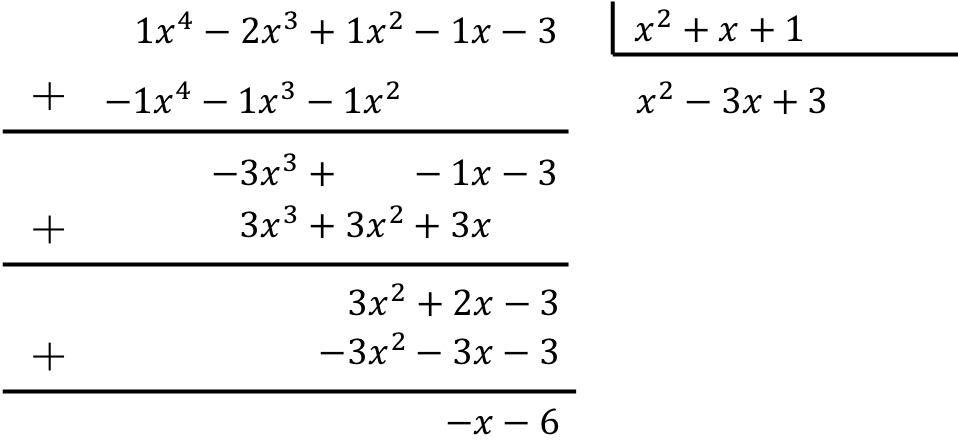
因此，两个多项式相除的结果是：
商：
休息：
👉👉👉如果您已经做到了这一步，这意味着您已经知道多项式如何除法。明亮的！现在您已经掌握了多项式除法，并且知道有一种方法可以让您更快地求解多项式之间的某些除法。这是一个合成除法或鲁菲尼规则，您可以通过点击链接来查看如何应用此技巧以及何时可以使用它。😉