在这里,您将找到它们是什么以及如何调用多项式的所有部分(次数、变量、独立项等)的解释。此外,您将能够看到几个示例并通过已解决的练习来练习多项式的部分内容。
但在了解多项式的各个部分之前,让我们快速回顾一下它的数学定义,以便充分理解这个概念:多项式是由不同次数的单项式相加或相减形成的代数表达式。
多项式由哪几部分组成?
多项式的各部分是:
- 项:多项式的每个单项式部分。
- 系数:多项式每一项的数字。
- 阶数:多项式变量的最大指数。
- 变量:是多项式所具有的字母。
- 主项:是多项式的最高次项。
- 独立项:不包含变量的多项式的项。
- 主系数:多项式主项的系数。
当多项式只有一个变量时,其次数等于其各项的最大指数。然而,如果多项式有两个或多个变量,则由于必须执行运算,因此更难以知道其次数。单击以下链接了解两个(或更多)变量多项式的次数,了解如何完成此操作。
如何识别多项式的各部分
多项式的各个部分或元素可以通过视觉轻松找到。如下图所示,看看这是如何完成的:
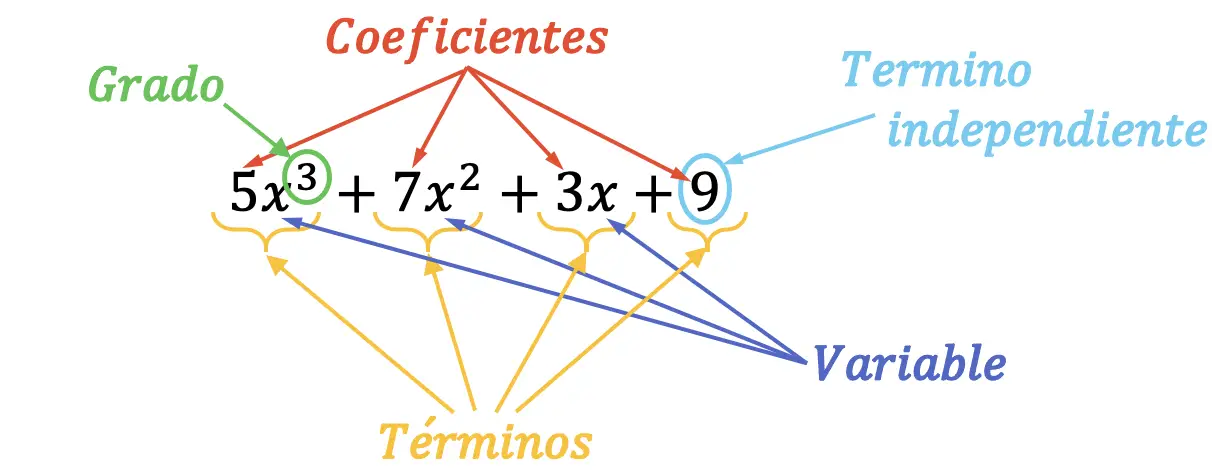
前面的三次多项式已标记其所有部分。另外,所述多项式的主项大约为5x 3 ,因为它是最高次的单项式。同样,多项式的首项系数为 5,因为它是首项的系数。
在这种情况下,多项式只有一个变量,因此只有一种类型的次数。但您应该知道,当多项式是多变量时,您必须区分变量的绝对次数和相对次数。您可以在我上面留给您的链接中查看它们各自的组成部分⬆⬆(两个变量的多项式的次数)。
多项式部分的示例
为了完全理解多项式各部分的含义及其执行的函数,我们将看到一些确定任何类型多项式各部分的示例:
实施例1
确定以下二次(2 次)多项式的各个部分:
![]()
- 项:4x 2 、-8x、1
- 系数:4、-8、1
- 第2年
- 变量 x
- 主要术语:4x 2
- 独立授权:1
- 转向系数:4
另一方面,应该注意的是,这个例子中的多项式被称为三项式。您可以在三项式的示例中了解这种类型的多项式是什么。此外,您可能还对另一种称为二项式的多项式感兴趣(用它做一些运算更容易),您可以在二项式示例中看到它的特别之处。
实施例2
找出以下多项式的部分:
![]()
- 项:y 3 、9y 2 、-5y、3
- 系数:1、9、-5、3
- 第3年
- 变量:和
- 主要术语: 和3
- 独立授权:3
- 转向系数:1
正如您在这个示例中看到的,当单项式前面没有数字时,这意味着它的系数是单位。因此该多项式的首项系数等于 1。
多项式各部分的解答练习
为了帮助您记住多项式所有部分的名称,我们为您准备了几个已解决的练习。您可以在评论中向我们询问有关它们的所有问题。 ⬇⬇
练习1
找出以下多项式的所有部分:
![]()
本练习中的多项式没有独立项,因为所有项均由至少一个变量(或字母)构成。
术语: 2×4、6×2 、 x
系数:2、6、1
4级
变量 x
主要术语: 2×4
独立术语:不
转向系数:2
练习2
找出以下多项式的所有部分:
![]()
该问题中的多项式由两个变量组成:x 和 y。然而:
项:-7x 4 y 2 、3x 4 、-5y 2 、xy、-10
系数:-7、3、-5、1、-10
第6年
变量:x、y
主要术语:-7x 4和2
独立授权:-10
转向系数:-7
正如您所看到的,要求解这样的多项式,您需要知道如何计算具有多个变量的多项式的次数。如果您仍然不确定如何执行此操作,我建议您查看上面的链接,多项式由哪些部分组成? (两个变量的多项式的次数)。 ⬆⬆ 您将找到分步说明以及几个示例。
尽管这是一个完全不同的概念,但如果您已经了解了这一步,您肯定也会对知道数字的多项式表达式是什么感兴趣。这是很多人不知道但实际上非常有用的东西。