在本页上,我们解释如何减去多项式。此外,您还将找到几个用于多项式减法的示例和已解决的分步练习。
多项式如何减法?
要减去两个多项式,必须减去相似多项式的项。换句话说,减多项式包括减去具有相同字面部分(相同变量和相同指数)的项。
在数学中,您可以通过两种不同的方式计算多项式的减法:垂直方法或水平方法。以下是这两个过程的说明,但我们建议您先学习如何垂直减去多项式,然后再学习水平方法。显然坚持你喜欢的那个。
垂直多项式的减法
接下来,我们将通过示例了解如何垂直减去两个多项式:
- 做减法
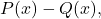
是两个多项式:
![]()
![]()
要找到多项式减法,我们需要做的第一件事是将一个多项式放在另一个多项式下面,以便两个多项式的相似项在列中对齐:
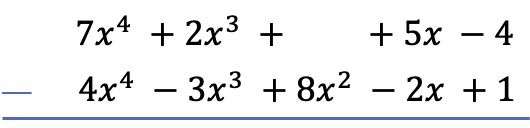
警告:如果多项式没有特定次数的项,则该空格必须留空。例如,多项式
![]()
没有二次单项式,所以它的位置有一个空格。
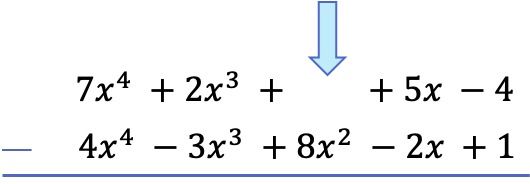
虽然我们现在可以直接对多项式进行减法,但是如果我们这样做的话很容易得到错误的符号。因此,要进行多项式减法,最好改变减法多项式(减法多项式)中所有项的符号,然后再进行加法。因为减去多项式与添加相反的多项式相同。
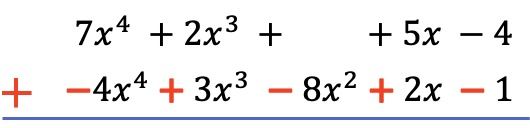
一旦我们按照从最高次到最低次的顺序排列所有项并否定下面多项式的项,我们就添加每列的系数,保持文字部分相等:
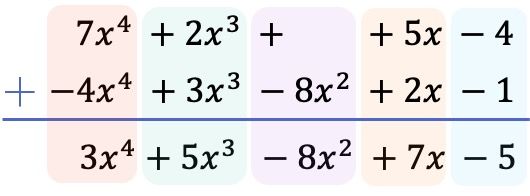
因此,2个多项式相减得到的结果为:
![]()
如果您不清楚最后一步,我将向您解释多项式的加法是如何完成的,事实上,掌握多项式的加法才能成功地减去多项式是至关重要的。在链接页面上,您还可以找到多项式加法的示例和已解决的练习,此外,您还可以看到多项式加法和减法之间的差异。
水平多项式的减法
我们刚刚了解了如何垂直地减去多项式,但现在我们将看到另一种用于减去多项式的方法:水平地减去多项式。这个过程肯定比前一个过程要快,但是需要对多项式的概念有很好的掌握。
那么让我们通过一个例子来看看这种多项式减法的方法是由什么组成的。因此您可以看到两种方法之间的差异,我们将减去与上一个示例中相同的多项式:
- 计算余数
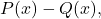
是两个多项式:
![]()
![]()
我们必须首先将两个多项式以代数运算的形式表示,即一个接一个:
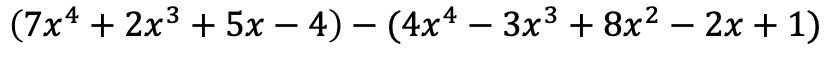
第一个括号中的单项式保持不变,但第二个括号中的项必须更改符号,因为它们前面有一个负数:
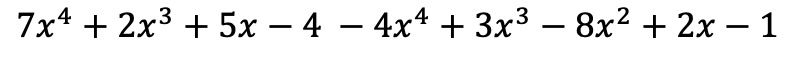
现在,我们将具有相同字面部分的术语分组,即具有相同变量(字母)和指数的术语。不相似的术语不能添加或删除。
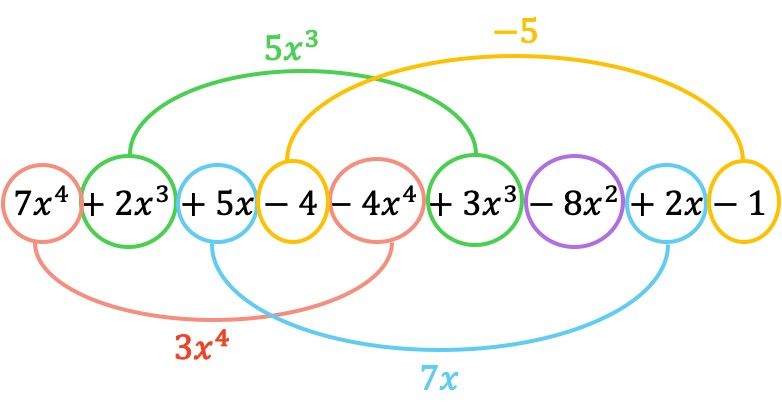
所以减法得到的多项式是:
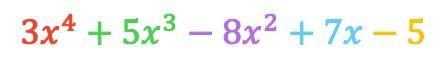
正如您所看到的,我们使用这两种方法得到了相同的结果,因此您可以使用最适合您的一种。
既然您已经了解了解决多项式减法的两种方法,您是否知道也可以用多项式进行分数减法?不仅仅是减法,还有各种运算。单击此链接了解如何使用代数分数进行运算。
解决了多项式减法问题
为了方便您进行练习,我们为您提供了几个已解决的多项式减法练习。如果您对练习有疑问,可以在页面评论中提出,我们会尽快解答。
练习1
减去多项式
![]()
减去多项式
![]()
![]()
![]()
在这种情况下,我们将垂直减去两个多项式。为此,我们首先按次数对多项式进行排序,然后更改其余多项式项的符号,最后将位于同一列的单项式相加:
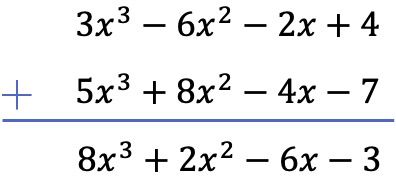
练习2
求解减法多项式
![]()
减去多项式
![]()
![]()
![]()
两个多项式相减相当于将相减多项式的相反数加到小型多项式上。因此,我们改变分包多项式(剩下的一项)项的符号并将多项式相加:
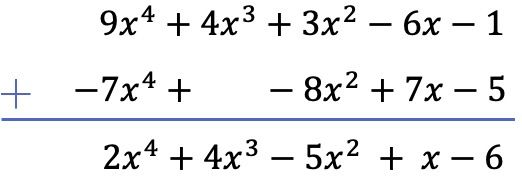
请注意,在这种特殊情况下,第二个多项式的 3 次列中必须留有一个空格,因为它没有三次项。
练习3
求多项式相减的结果
![]()
减去多项式
![]()
![]()
![]()
在这种情况下,我们将垂直求解两个多项式的减法。因此,首先我们将多项式按从最大次数到最小次数的顺序排列,然后更改其余多项式项的符号,最后添加类似项:
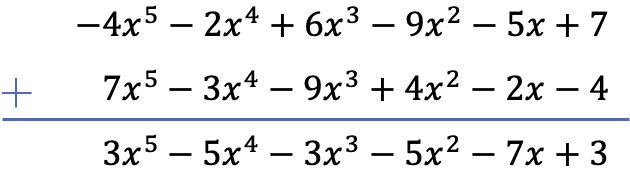
练习4
用多项式计算以下运算:
![]()
![]()
![]()
![]()
在这种情况下,涉及3个多项式进行运算,其中2个是减法。因此,为了解决该运算,我们将更改其余两个多项式的所有项的符号,然后将多项式相加。
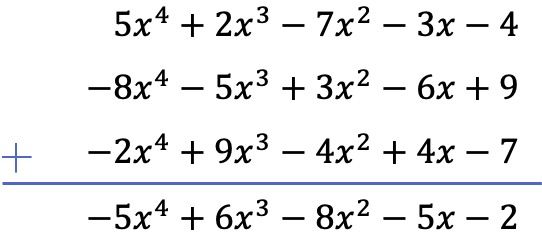
你觉得这个解释怎么样?你觉得有用吗?您更喜欢哪种多项式减法,垂直还是水平?我们在评论中读到了你! 👀