在此页面上,您将找到圆锥曲线的定义、为什么它们如此重要以及存在的不同类型的圆锥曲线(圆、椭圆、双曲线和抛物线)。此外,您将能够看到它们的方程之间的差异。
什么是圆锥曲线?
在解析几何中,圆锥曲线(或简称圆锥曲线)是圆锥体与平面之间的不同交点(当该平面不通过圆锥体的顶点时)产生的所有曲线。圆锥曲线有四种类型:圆、椭圆、抛物线和双曲线。
以下是可以从任何圆锥体获得的 4 个可能的截面:
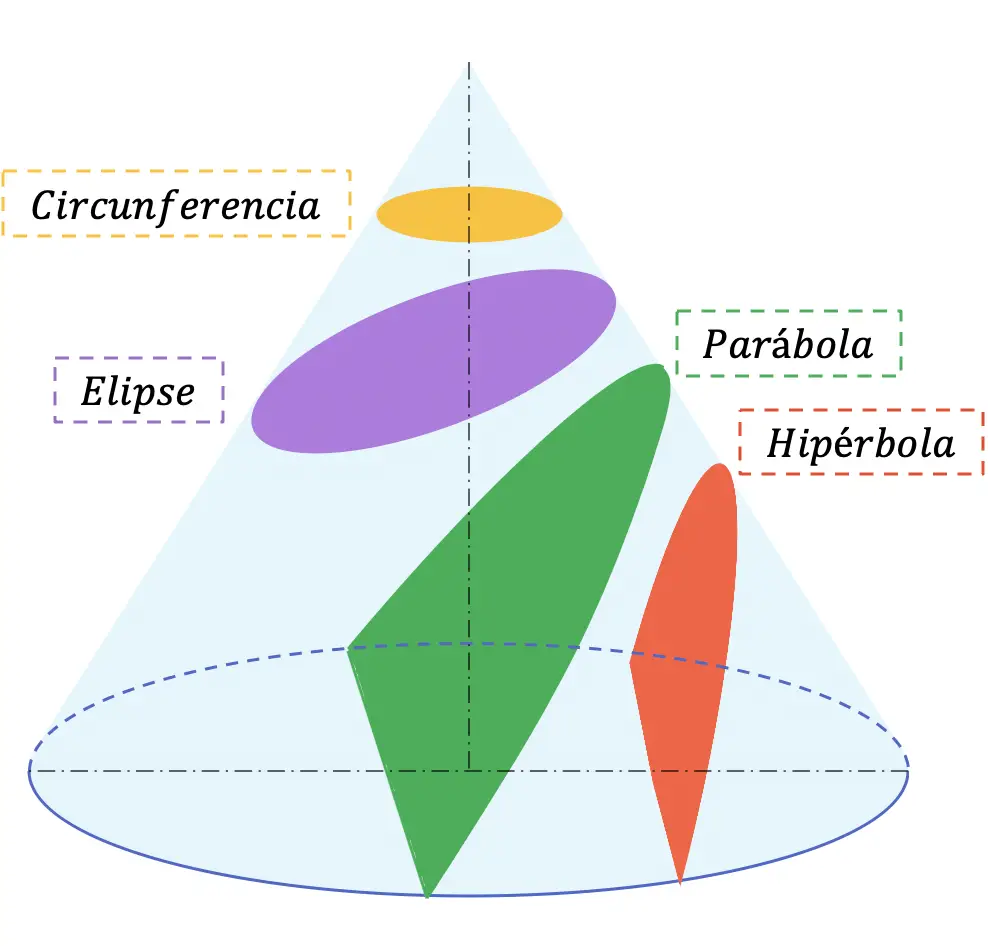
圆锥曲线通常在中学(Bachillerato)的数学和技术制图科目中学习。
圆锥曲线的类型
了解了圆锥曲线的概念后,让我们看看存在的四种圆锥曲线是什么:圆、椭圆、抛物线和双曲线。
圆周
圆周是圆锥形截面,可以通过用垂直于其旋转轴(平行于底面)的平面切割圆锥体来找到。

此外,圆周是平面上与称为中心的固定点等距的点的轨迹。
椭圆
椭圆是一条平坦的、封闭的、与圆周非常相似的曲线,但它的形状更呈椭圆形。特别是,它是由斜面切割圆锥体表面而产生的,该斜面相对于旋转轴的角度大于发电机的角度。
另外,椭圆的所有点都满足一个条件:该椭圆是平面上所有点到另外两个固定点(称为焦点F和F’)的距离之和为常数的轨迹。

寓言
在数学中,抛物线是平面上与固定点(称为焦点)和固定线(称为准线)等距的点的轨迹。

在几何上,抛物线是圆锥体被平面截断的结果,该平面相对于旋转轴的倾角等于圆锥体母线的角度。因此,包含抛物线的平面平行于圆锥体的母线。
该圆锥曲线的一个非常重要的特征是抛物线方程,因为根据其状态,我们可以确定它是什么类型的抛物线。在此链接中,您将找到抛物线的所有方程、抛物线的元素是什么、它们的属性、示例、已解决的练习……以及抛物线的其他特征。
双曲线
作为圆锥曲线,当用平面切割圆锥体时,所得到的双曲线的角度小于圆锥体的母线相对于其旋转轴所形成的角度。
从数学上讲,双曲线可以定义为平面上满足以下性质的点的轨迹:双曲线上任意点与两个固定点(称为焦点)之间的距离差的绝对值必须恒定。
此外,这两个距离相减的值始终等于双曲线两个顶点之间的距离。
![]()

我确信您已经推断出,参数值
![]()
双曲线的基本原理是双曲线的基础。在下面的链接中,您可以看到我们对双曲线的解释,您可以在其中找到为什么它是一个如此重要的系数以及表征双曲线的所有元素。另外,您还会发现双曲线的方程是什么样子、存在的不同类型的双曲线,甚至还有关于双曲线的分步问题和练习。
圆锥曲线的一般方程
每个圆锥曲线都可以解析地表达为方程。事实上,所有二次曲线方程都必须是二阶方程:
![]()
因此,至少有一个系数
![]()
任何一个
![]()
公式的值必须非零。
因此,根据参数值,方程将对应于一种或另一种二次曲线:
- 周长:对于描述周长的一般方程,以下项

和

必须匹配并且

必须为零。
![]()
- Ellipse :当满足以下条件时,该方程将对应于椭圆的数学表达式:
![]()
- 抛物线:要使方程成为抛物线,必须满足以下等式:
![]()
- 双曲线:最后,双曲线的一般方程必须满足以下不等式:
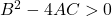 文章导航
文章导航