在此页面上,您将找到有关圆周方程的所有内容:普通方程、一般方程、其他类型的圆周方程、何时圆周方程正确……此外,您还将看到如何找到方程的示例圆周,您可以通过已解决的练习进行练习。
普通圆方程
在了解什么是周长方程之前,我们先回顾一下周长的概念:
圆周是平面上与称为中心的固定点等距的点的轨迹。

因此,圆上的所有点到圆心的距离都相同。
此外,圆是与椭圆、抛物线和双曲线一起的四个圆锥曲线之一。即用平行于底面的平面切割圆锥体即可得到圆。
在笛卡尔平面中描述圆的最简单方法是根据其普通方程。因此,周长常方程的公式如下:
圆的普通方程为:
![]()
金子:
-

是圆的半径。
-

和

是圆心的坐标:
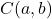
虽然我们不会演示它,因为它有点乏味,但这个方程可以从毕达哥拉斯定理得到。
我们通过一个例子来看看圆的常方程是如何计算的:
- 求以该点为圆心、半径为5的圆的常方程
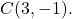
圆的普通方程的公式为:
![]()
因此,我们只需要用未知数来代替
![]()
由半径值和未知数
![]()
和
![]()
分别由圆心的 X 和 Y 坐标:
![]()
所以圆的普通方程为:
![]()
圆的一般方程
另一种圆周方程是一般方程,实际上它是最常用的。然后我们将看到如何从任何圆周的常方程中获得其一般方程。
考虑圆的普通方程:
![]()
如果我们开发出卓越的等式(或卓越的产品):
![]()
![]()
现在我们对变量进行 3 处更改:
![]()
最终我们得到圆周的一般方程:
![]()
因此,周长一般方程的公式为:
![]()
其中圆心是:
![]()
圆的半径为:
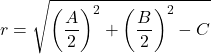
所以这个圆周方程总是由普通方程得到。下面是一个例子来看看它是如何完成的:
- 求以该点为圆心、半径为6的圆的一般方程
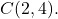
首先我们需要找到圆的普通方程。为此,我们使用他的公式:
![]()
![]()
现在我们进行操作,直到找到圆周的一般方程,也就是说,直到我们无法再简化:
![]()
![]()
![]()
![]()
所以圆的一般方程为:
![]()
虽然问题没有要求,但我们现在可以计算找到的方程的圆心和半径来验证它是否正确。
为了确定圆的中心,我们使用它的公式:
![]()
![]()
![]()
![]()
事实上,圆心与声明的中心重合。
我们还用公式检查圆周的半径:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png)
并且半径也等于语句的半径。因此,计算出的周长方程是正确的。
圆周的存在性
所有方程的形式为
![]()
对应一个圆。因此,要使此类表达式真正成为圆方程,必须满足以下 3 个条件:
- 的系数
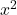
和的
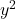
它们必须等于 1。请记住,如果两个变量前面都有一个不是 1 的数字,但它们具有相同的数字,则整个方程可以除以该数字,以便它们的系数为 1。
- 方程不能有项
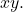
- 以下表达式必须为正:
 其他类型的圆方程
其他类型的圆方程
我们见过的两个圆方程,即普通方程和一般方程,最常用于在数学上表达平面上的圆(在 R2 中)。然而,有几种类型的方程来描述这个几何对象,下面是每种方程的解释。
圆的正则方程
圆的正则方程或简化方程用于描述其中心位于坐标原点(即点 (0,0))的任何圆。所述方程如下:
![]()
另外,如果半径等于单位(1),则周长方程将为:
![]()
最后一个方程对应于测角周长,也称为单位周长或单位圆。它是以坐标原点为圆心、半径为 1 的圆。
两个同心圆的方程
两个同心方程是中心在同一点的方程。两个同心圆唯一不同的是半径。
因此,要满足这个条件,两个同心圆的方程除了独立项必须不同之外,完全相同。
![]()
![]()
例如,以下两个圆是同心的,因为除了独立项之外,它们的所有系数都相同:
![]()
![]()
圆的参数方程
与直线一样,圆的方程也可以用正弦和余弦的三角函数来参数化。因此,圆的参数方程为:
![Rendered by QuickLaTeX.com \diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png)
点在哪里
![]()
是圆的中心并且
![]()
这是你的部门。
解决了圆的方程问题
练习1
计算以点为圆心、半径为5的圆的一般方程
![]()
要求圆的一般方程,首先要求它的常方程。为此,我们使用圆的普通方程的公式:
![]()
![]()
![]()
一旦我们知道了普通方程,我们就可以找到圆的一般方程:
![]()
![]()
![]()
![]()
所以圆的一般方程为:
![]()
练习2
对于以下每个圆,找到其圆心的坐标和半径的长度。
![]()
![]()
![]()
周长A)
![]()
周长以常方程的形式表示,其公式为:
![]()
因此,圆心坐标为:
![]()
![]()
其半径为:
![]()
![]()
周长 B)
![]()
该周长以一般方程的形式表示,因此要计算其中心的坐标,必须使用以下公式:
![]()
![]()
![]()
![]()
另一方面,求圆半径的公式是:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png)
周长C)
![]()
周长以常方程的形式表示,其公式为:
![]()
因此,圆心坐标为:
![]()
在这种情况下,方程没有项。
![]()
两者都不
![]()
因此它以坐标原点为中心:
![]()
其半径为:
![]()
![]()
练习3
下列哪个方程是圆的方程?
![]()
![]()
![]()
![]()
对于圆方程的表达式,必须满足以下条件:
1.系数
![]()
和的
![]()
它们必须等于 1。
2.方程不能有项
![]()
3.
 因此,我们必须验证每个方程是否满足这三个条件。
因此,我们必须验证每个方程是否满足这三个条件。
方程A)
![]()
的系数
![]()
和
![]()
为 1 并且方程没有项
![]()
因此,检查第三个条件就足够了:

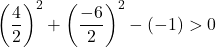
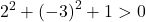
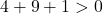
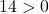 该方程满足3个条件,故为圆方程。
该方程满足3个条件,故为圆方程。
方程 B)
![]()
该方程有一个项
![]()
其中方程不对应于圆。
方程C)
![]()
的系数
![]()
和
![]()
不是 1,但我们可以通过除以所有项来变换方程:
![]()
这样现在的系数
![]()
和
![]()
是的,它们是 1,而且,方程没有项
![]()
因此我们只需验证第三个条件:

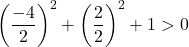
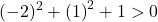
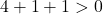
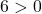 该方程满足3个条件,故为圆方程。
该方程满足3个条件,故为圆方程。
方程 D)
![]()
的系数
![]()
和
![]()
为 1 并且方程没有项
![]()
因此,检查第三个条件就足够了:

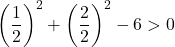
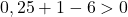
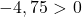 该方程不满足最后一个条件,因此它不是圆的方程。
该方程不满足最后一个条件,因此它不是圆的方程。
练习4
确定经过下列三点的圆的方程:
![]()
任意圆的一般方程为:
![]()
因此,我们需要将点的坐标代入圆方程来求参数
![]()
![]()
和
![]()
通过第一点我们找到系数
![]()
![]()
根据第二点我们求出系数
![]()
![Rendered by QuickLaTeX.com \begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png)
从第三点我们求出系数
![]()
![Rendered by QuickLaTeX.com \begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png)
总之,周长的一般方程为:
![]()
练习5
如果圆的两端是以下两点:
![]()
圆的普通方程是什么?
如果这两点是圆的端点,则圆心将是这两点之间的中点:
![]()
![]()
![]()
另一方面,圆的直径将是两点之间的距离,可以使用两点形成的矢量的大小来计算:
![]()
![]()
圆的半径是直径的一半:
![]()
因此,圆的普通方程为:
![]()
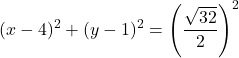
![]()
最后,如果本文对您有用,您肯定也会对我们的双曲线(数学)和抛物线(数学)页面感兴趣。您将找到关于双曲线和抛物线是什么、它们的方程、它们的特征、示例、已解决的练习的详细解释……