向量乘以数字

本页说明如何以数字和图形方式将向量乘以实数（或标量）。此外，您还将找到向量与标量乘积的示例和已解决的练习。最后，还解释了这种向量运算的性质。

如何将向量乘以实数？

因此，向量乘以数字的结果会产生具有以下特征的新向量：

• 向量与标量相乘的结果会产生一个与原始向量方向相同的新向量。
• 此外，如果数字为正，则新向量将具有相同的方向。
• 否则，如果该数为负数，则其含义相反。
• 结果向量的大小等于原始向量的大小乘以标量。

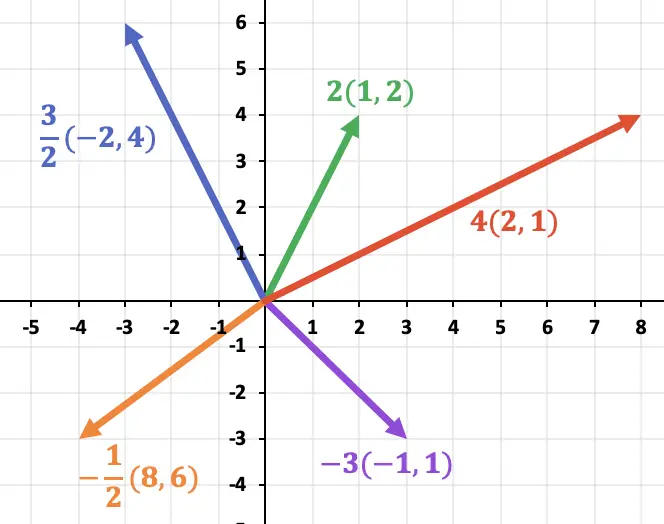
在下图中，您可以看到无论标量的符号如何，如何保持矢量的方向。另一方面，向量的方向取决于它相乘的数字的符号。

此外，在下图中可以清楚地看到，所得乘积向量的大小等于原始向量的大小乘以标量。

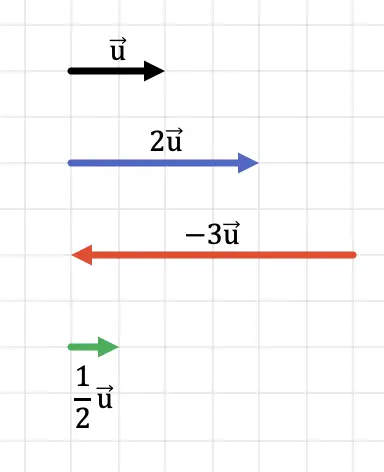
显然，如果我们将向量乘以大于 1 的数字，结果将是一个长度更大（模数更大）的向量。另一方面，如果我们将向量乘以小于 1 的数，则结果是长度较短（模数较小）的向量。

注意：不要将向量和 标量的乘积与向量的点积混淆。虽然它们的名字相似，但它们是两个完全不同的概念。

向量与标量的乘积示例

接下来，我们将看到一个数值示例，说明如何计算向量和数字的乘积：

• 将以下向量乘以 4：

正如您所看到的，这种类型的向量运算并不是很复杂，因为您不必进行大量计算。

然而，还有更复杂的向量运算，例如向量加法和向量减法。如果您已经了解如何计算向量和标量的乘积，我们建议您进入下一个级别，看看如何求解 向量加法和向量减法，因为这些运算有些困难，事实上，它们被使用得更多（它们更重要）。

向量乘以数字的性质

向量和数字的乘积具有以下属性：

• 结合性：当向量乘以多个数时，乘法的顺序并不重要。

• 关于向量加法和减法的分配律：

• 关于标量相加的分配性质：

• 中性元素：显然，任何向量乘以1都会得到向量本身：

解决了向量与标量相乘的问题

练习1

解析计算以下向量与 3 的乘积结果：

要求乘积，必须将向量的每个坐标乘以 3：

练习2

将以下向量乘以 6 并找到其模：

我们首先将向量乘以标量：

现在有两种方法来计算所获得的向量的大小。首先是找到原始向量的大小，然后将其乘以 6：

第二种方式是直接计算相乘得到的向量的大小：

因此，这两个过程都表明结果不依赖于计算模量的方法。

练习3

从以下向量：

以代数方式计算以下运算：

接下来判断得到的向量是否与原向量具有相同的方向和方向，并按照从最短到最长的顺序排列。

我们首先计算乘法：

因此，向量乘以正数，其方向和方向与原向量相同。向量乘以负数与原向量方向相同但方向相反。

同方向和同方向的向量：

和

方向相同但含义不同的向量：

最后，我们必须根据向量的长度或等效的模数对向量进行排序。最长长度（或最大模块）的向量将是乘以较大数（绝对值）的向量，最短长度（或最小模块）的向量将是已乘以较小数的向量数量（绝对值）。所以长度的顺序是：

请注意，长度或模数不取决于相乘标量的符号，因为矢量的方向不会修改其模数。

练习4

考虑以下两个向量：

计算如下运算：

我们首先解决向量与数字的乘法：

然后我们减去向量：

练习5

执行以下向量与标量的乘法并绘制结果：

我们首先将向量乘以实标量：

最后，一旦我们计算了向量，我们就将它们表示在图中：