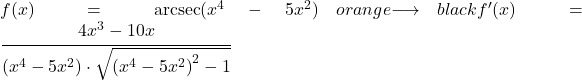在此页面上,您将看到反正割(公式)的导数是什么。您将找到函数反正切导数的已解决练习。
反正割导数公式
x 反正割的导数是 x 乘以 x 平方根减 1 的乘积 1。
![]()
因此,函数反正割的导数等于该函数的导数除以该函数的商乘以该函数的平方根减一。
![]()
显然,第二个公式与第一个公式类似,两者之间唯一的区别是第二个公式中应用了链式法则。

尽管这看起来很奇怪,因为它们是反函数,但反正割的导数与正割的导数无关。您可以点击此处查看正割导数的公式:
➤参见:割线的导数
反正割导数的示例
实施例1
在这个例子中,我们将看到线性函数 7x 的反正切值的导数是多少。
![]()
要求反正割的导数,您必须应用其相应的公式,如下所示:
![]()
7x 函数的导数为 7,因此 7x 函数的反正切值的导数为:
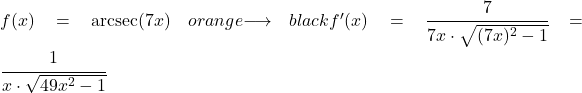
实施例2
在第二个示例中,我们将导出势函数的反正割。
![]()
由于反正割函数的参数中存在 x 以外的项,因此我们需要应用反正割导数规则和链式法则来推导整个函数。
![]()
因此,在分子中我们写下函数自变量的导数,在分母中我们重写势函数并将其乘以自变量函数的 2 减 1 次方的平方根: