反正切的导数

在本文中，您将学习如何导出函数的反正切。此外，您将能够看到此类导数的示例，甚至可以练习反正切导数的已解决练习。最后，我们还向您展示反正切导数公式的证明。

反正切的导数是什么？

x 反正切的导数是一加 x 平方的一分之一。

因此，函数反正切的导数等于该函数的导数除以一加上该函数的平方所得的商。

在本例中，函数由 au 表示，因此这将是函数 u 反正切的导数公式。

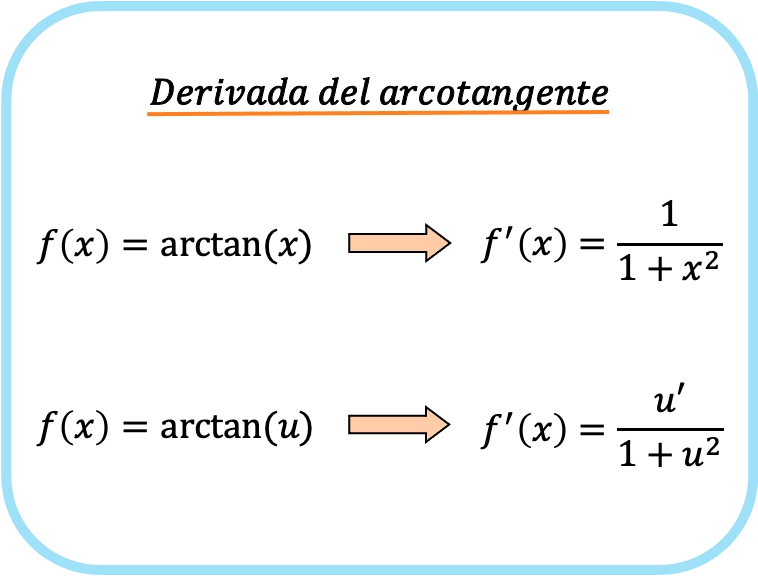
正如您所看到的，反正切的导数公式与反正弦和反余弦的导数公式非常相似。

反正切导数的示例

一旦我们知道了反正切导数的公式，我们将解释此类三角导数的几个例子的推导。这样，您会更容易理解函数的反正切是如何导出的。

示例 1：2x 反正切的导数

我们应用公式来求解导数：

2x 的导数为 2，因此 2x 的反正切导数为 2 除以 1 加 2x 的平方：

示例 2：x 平方的反正切值的导数

为了求出本例的导数结果，我们需要使用反正切导数的公式，即：

因此，函数 x ²的导数为 2x，因此 x 的反正切值的 2 次方的导数为：

示例 3：x 的正弦值的反正切导数

从逻辑上讲，要计算导数，您必须应用相应的公式：

在这种情况下，我们有一个复合函数，因此我们必须应用链式法则来计算反正切的导数：

已解决反正切导数的练习

推导以下反正切函数：

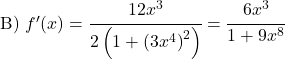
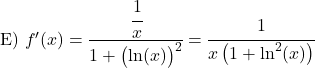
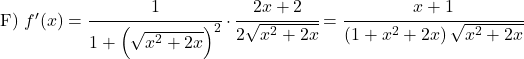
反正切导数公式演示

接下来我们来证明反正切导数的公式。

我们首先利用反正切是正切的反函数这一事实将反正切转换为正切：

我们对等式两边求微分：

我们删除和’：

另一方面，由于基本的三角恒等式，我们知道正弦和余弦的平方和等于 1。因此，我们可以将前面的表达式转换为分数：

我们将所有项除以余弦的平方：

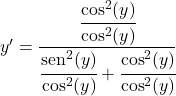
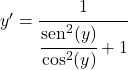
正弦除以余弦等于正切，因此：

正如我们在上面看到的，正切相当于变量x，因此我们可以代入表达式得出反正切导数的公式：