在这里,您将找到有关双曲线的所有内容:它是什么、它的特征元素是什么、如何找到它的方程、示例、已解答的练习等。
什么是夸张?
双曲线是一条有两个分支的开曲线,其数学定义如下:
在解析几何中,双曲线是平面上满足以下条件的点的轨迹:双曲线上的任意点与两个固定点(称为焦点)之间的距离差的绝对值必须恒定。
此外,这两个距离相减的值始终等于双曲线两个顶点之间的距离。
![]()

下面我们来看看系数的含义
![]()
一个夸张的说法。
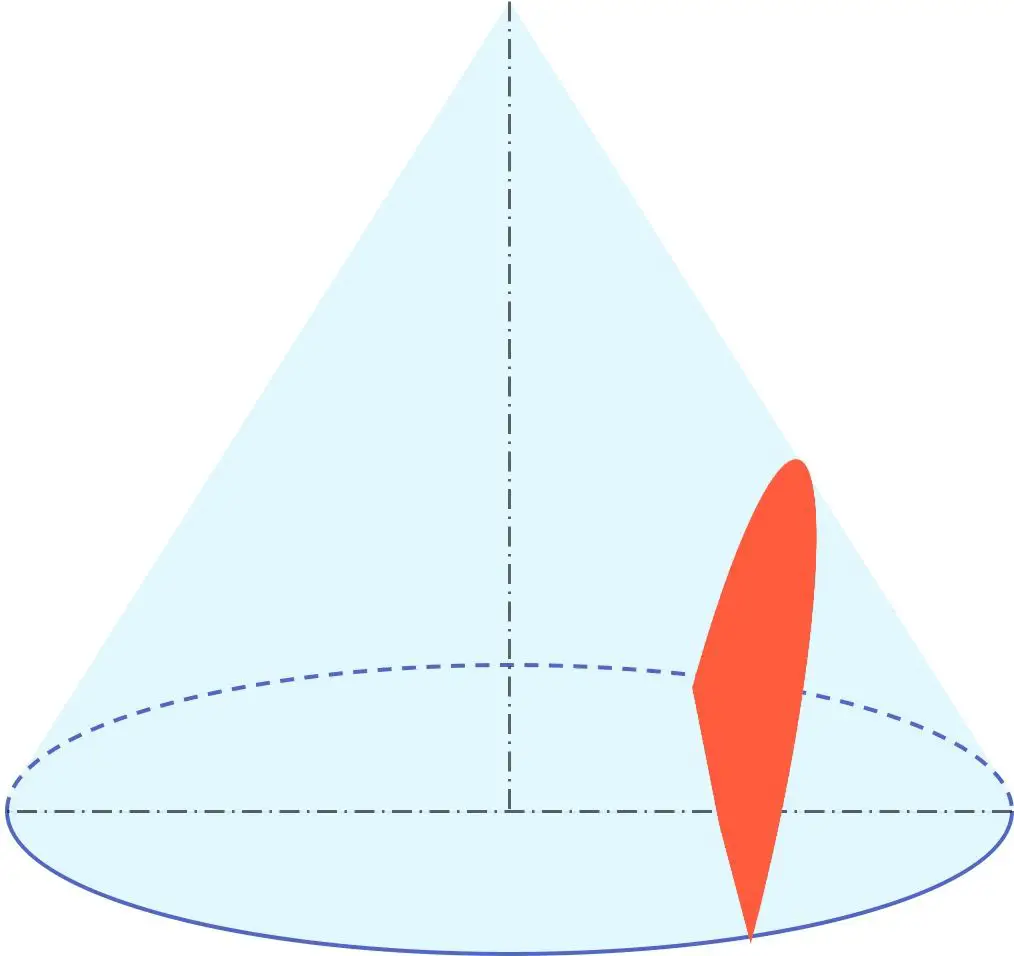
此外,双曲线与圆周、椭圆和抛物线一起属于称为二次曲线的几何群的一部分。因此,双曲线是圆锥曲线,或者换句话说,它可以由圆锥得到。
特别地,双曲线是圆锥体被平面截断的结果,该平面的角度小于圆锥体的母线相对于其旋转轴形成的角度。
双曲线的要素
双曲线的特征取决于以下因素:
- 焦点:这是每个双曲线的两个固定点特征(下图中的点 F 和 F’)。双曲线任意点到每个焦点的距离差的绝对值恒定且等于

- 焦点或主轴:穿过双曲线两个焦点的线。它对应于所述几何图形的对称轴。也称为横轴或横轴。
- 次轴:它是线段 FF’ 的平分线(通过点 B 和 B’ 的线)。另外,它是一条垂直于焦轴的线,它是双曲线的另一个对称轴
- 中心(O) :是两个轴的交点以及两个顶点和两个焦点的中点。由于双曲线有两个对称轴,因此它也是对称中心。
- 顶点(A和A’) :是双曲线的分支与焦轴的交点。
- 矢量射线 (R) :这些是从双曲线上的任意点到每个焦点的线段。
- 焦距:这是两个焦点之间的复合段的长度。
- 长轴或实轴:从A点到A’点的线段,其长度等于

- 小轴或虚轴:从B点到B’点的线段,其长度等于
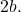
- 渐近线:是图表上显示的虚线。我们将在下面看到它们是如何计算的。
双曲线各元素之间的关系
首先我们说的半轴是指半个轴。例如,真半轴是从A点到双曲线中心的线段,其长度为
![]()
因此,实半轴、虚半轴和半焦距之间存在着非常重要的关系。事实上,我们接下来要推导的公式被大量用于解决双曲线练习和问题。
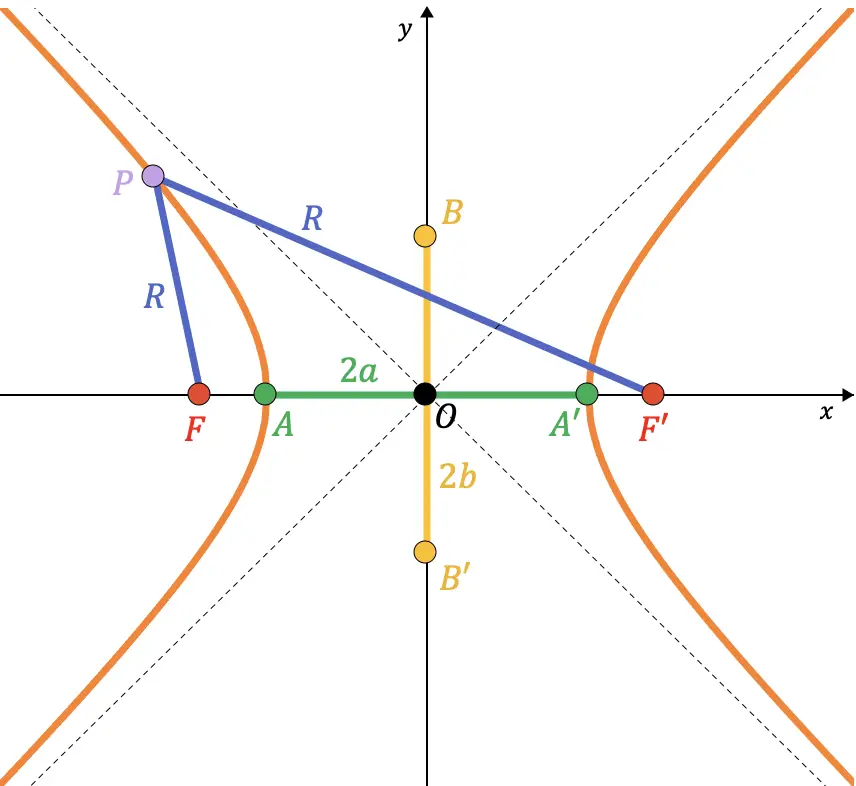
要知道,双曲线的 B 点和 B’ 点对应于主轴与假想半径圆的交点
![]()
从中心到 A 点(半焦距)。因此,正如您在下面的图形表示中看到的,连接 A 点和 B 点的线段与所述圆的半径重合(
![]()
):
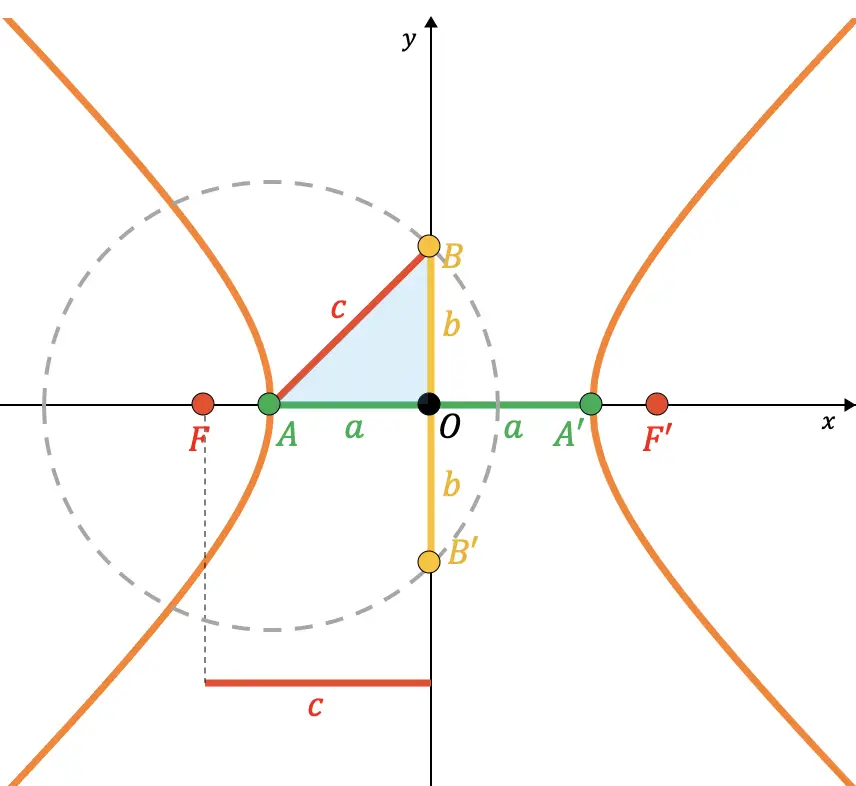
因此由毕达哥拉斯定理可以证明参数之间的关系
![]()
和
![]()
如下:
![]()
双曲线方程
双曲线方程有多种类型,因为根据其性质,可以使用其中一种或另一种来以数学方式表达它。接下来,我们将逐一详细分析。
首先,我们有双曲线的普通方程。其次,我们将看到普通方程的一个变体,这是双曲线的简化方程或正则方程。接下来,我们将研究双曲线的一般方程是如何的。最后,我们将分析双曲线的两种特殊情况的方程:等边双曲线和共轭双曲线。
普通双曲线方程
当我们想要通过方程定义一条外心位于坐标原点(点(0,0))的双曲线时,我们必须使用以下公式:
笛卡尔坐标系中双曲线的常方程的公式如下:
![]()
金子:
-

和

是双曲线中心的坐标:
-

是双曲线的半长轴的长度。
-

是双曲线的短半轴的长度。
通过这个方程,您可以描述焦轴为水平的双曲线(向左和向右打开的分支),这就是通常的双曲线。但是,如果我们使用垂直焦轴(从上到下打开的分支),则负号从变量 y 传递到变量x :
![]()
金子
![]()
和
![]()
和以前一样,是双曲线中心的坐标和项
![]()
和
![]()
它们仍然是双曲线的半长轴和半短轴,尽管与以前不同,这两个轴现在将分别垂直和水平定向。
双曲线的正则方程或简化方程
这类双曲线方程与普通方程非常相似,唯一的区别是正则方程用于解析表达以点(0,0)为中心的双曲线。因此,当双曲线的中心是坐标原点时,我们使用双曲线的正则方程或简化方程。
现在我们将根据双曲线的常方程推导出双曲线简化方程的公式:
![]()
如果双曲线的中心应为坐标原点,即点 (0,0),则以下情况始终为真:
![]()
![]()
因此,双曲线的规范或简化方程公式将是:
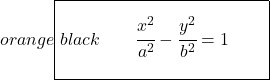
和之前一样,如果焦轴是垂直的而不是水平的,则负变量将为x :
![]()
双曲线的一般方程
双曲线的一般方程的公式如下:
![]()
然而,为了使上式成为双曲线,系数
![]()
和
![]()
它们必须不同于零,同时具有相反的符号。
等边双曲线方程
等边双曲线是实半轴长度等于虚半轴长度的双曲线,这意味着
![]()
因此,等边双曲线的方程为:
![]()
此外,等边双曲线的渐近线彼此垂直。这些线的方程如下:
![]()
![]()
如果我们仔细观察,这两个方程分别是第一(和第三)象限和第二(和第四)象限的平分线。因此,如果我们将等边双曲线向左旋转 45°,则它的渐近线占据坐标轴的位置:
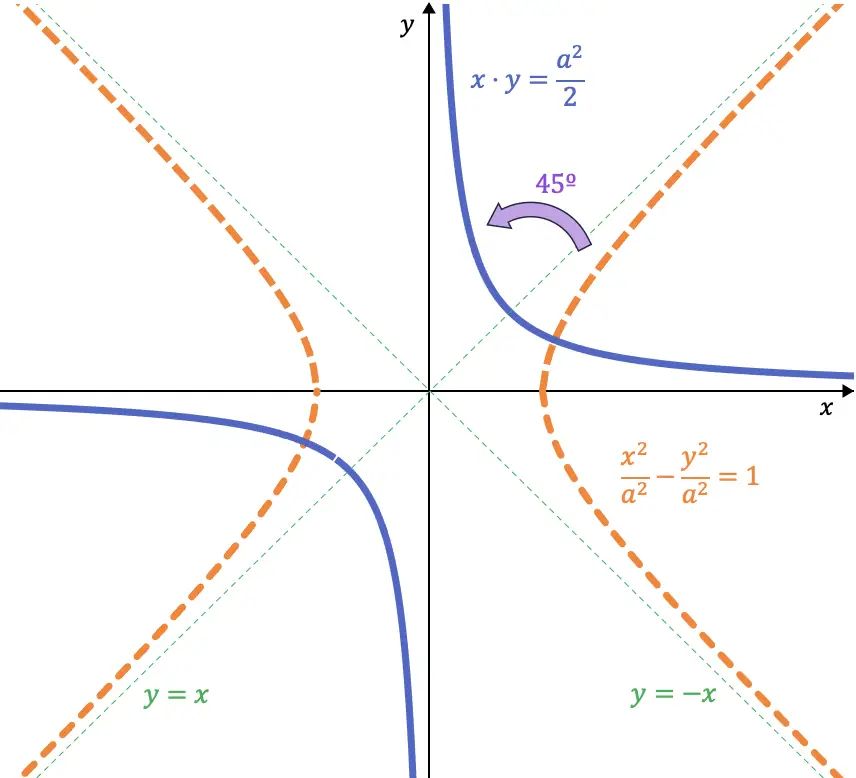
因此,当我们进行 45° 转弯时,双曲线的方程为:
![]()
共轭双曲线
如果一条双曲线的实轴等于另一条双曲线的虚轴,则两条双曲线是共轭的。因此,两个共轭双曲线方程之间的唯一区别在于哪个变量被否定,因为分母的系数必须保持相同。
这是两个彼此共轭的双曲线方程的示例:
![]()
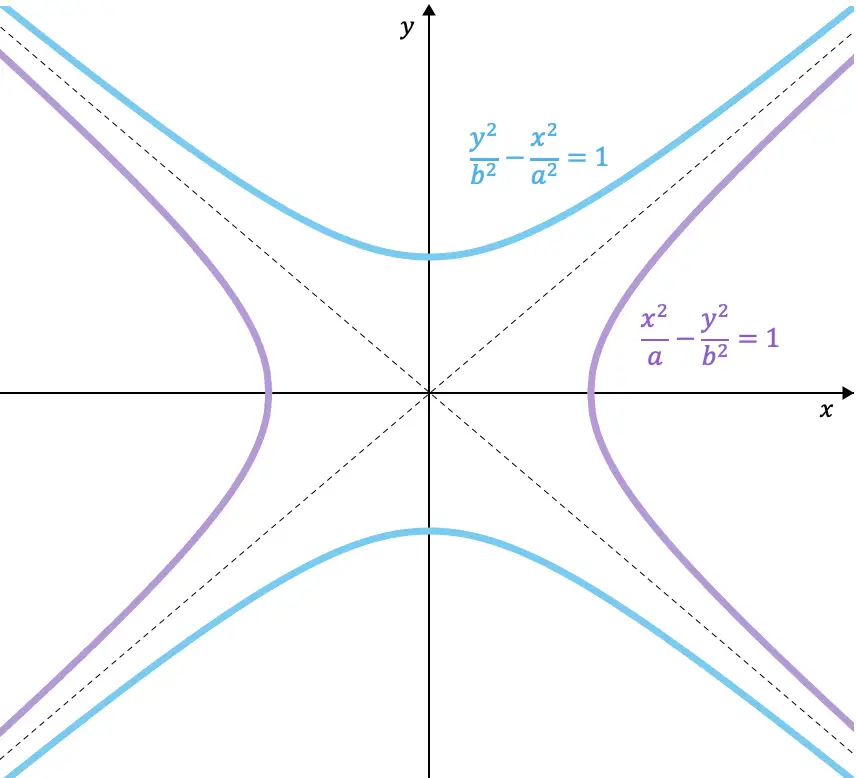
此外,从绘制的双曲线中可以看出,共轭双曲线具有相同的渐近线。
双曲线的渐近线
正如您在前面的图表中看到的,每个双曲线都有两条渐近线。请记住,渐近线是一条非常接近函数但从未完全相交或接触的直线。
因此,对应于双曲线渐近线的公式是:
![]()
![]()
这样任何双曲线的渐近线都可以使用它们的系数轻松确定
![]()
和
![]()
分别是双曲线的实半轴和虚半轴的长度。
双曲线的偏心率
双曲线的偏心率是决定其开放或闭合程度的特征参数。在数值上,双曲线的偏心率是通过将其半焦距除以其实半轴来计算的:
![]()
任何双曲线的偏心率总是大于 1:
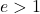
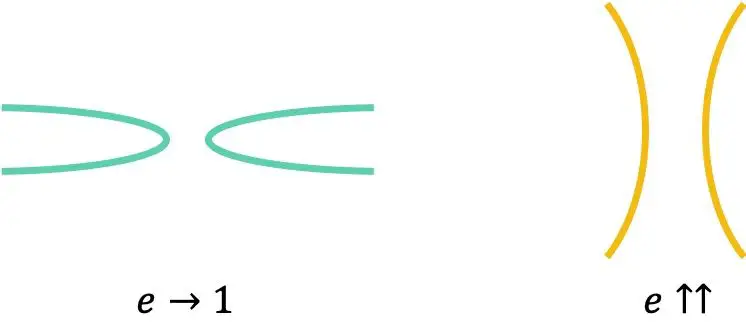
最后,应该注意的是,等边双曲线的偏心率始终等于
![]()
双曲线问题已解决
下面你可以练习我们在双曲线和双曲线方程的问题和已解决的练习中看到的概念。
练习1
以(-1.3)为中心、实半轴长度为3个单位、虚半轴(平行于Y轴)长度为7个单位的双曲线方程是什么?
要找到双曲线方程,只需应用双曲线常方程的公式:
![]()
我们将双曲线中心坐标代入方程:
![]()
![]()
最后,我们替换未知数的值
![]()
和
![]()
![]()
![]()
练习2
求双曲线的中心、顶点、焦点、偏心率值和渐近线的坐标,其方程定义为:
![]()
首先,需要注意的是,方程中的负变量是变量y ,因此双曲线的分支将向右和向左打开(焦轴平行于 X 轴)。
其次,该方程对应于双曲线的正则(或简化)方程,因此其中心是坐标原点。
![]()
一旦我们知道了双曲线的中心,为了计算其他所有内容,我们需要找到实半轴的值(参数
![]()
)和虚半轴(参数
![]()
)。我们可以从双曲线的正则(或简化)方程的公式中推导出两者:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
因此,如果中心和顶点之间的距离为 5 个单位,则意味着双曲线的顶点为:
![]()
要确定每个焦点的坐标,必须知道半焦距的值(参数
![]()
)。为此,我们可以使用连接双曲线元素的公式:
![]()
![]()
![]()
因此,中心和住宅之间有 13 个单位的空间。因此,每户的坐标为:
![]()
那么,要计算双曲线的偏心率,我们需要使用其相应的公式:
![]()
最后,我们找到双曲线的渐近线及其公式:
![]()
![]()
练习3
已知双曲线上一点到焦点 F(-4.0) 和 F(4.0) 的距离差为 6 个单位,计算以坐标原点为中心的双曲线方程。
首先,由于双曲线的中心位于坐标原点,因此我们将使用规范或简化方程:
![]()
那么,根据双曲线的定义,它的一个点到焦点的距离差的绝对值(在本例中为 6)必须等于实轴的长度(
![]()
)。然而:
![]()
![]()
![]()
![]()
另一方面,双曲线的中心是点(0,0),焦点是点(4,0)。使得到两点的距离(参数
![]()
) 为 4 个单位。
![]()
我们现在可以知道参数的值
![]()
双曲线的3个特征系数之间的数学关系:
![]()
![]()
![]()
![]()
所以双曲线的方程为:
![]()
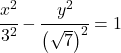
![]()