在此页面上,您将了解什么是卷积矩阵。我们还向您展示尺寸为 2×2、3×3 和 4×4 的对合矩阵的示例。最后,您将找到对合矩阵的公式。
什么是对合矩阵?
卷积矩阵的含义如下:
卷积矩阵的定义:可逆方阵,其逆矩阵是矩阵本身。
![]()
金子
![]()
是任意矩阵并且
![]()
表示其倒数。
显然,对合矩阵是正则或非简并矩阵的一个例子。
如果您不知道什么是矩阵的逆矩阵,可以在此处查看如何计算3×3 逆矩阵。了解如何反转矩阵很重要,但是为此您还需要知道如何计算矩阵的伴随。
但回到主题:当矩阵是对合矩阵时,矩阵与矩阵本身相乘得到单位矩阵。看看演示:
任何矩阵乘以它的逆矩阵都会得到单位(或单位)矩阵。所以:
![]()
并且由于对合矩阵的逆是矩阵本身:
![]()
因此,平方卷积矩阵给出单位矩阵:
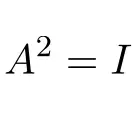
卷积矩阵的示例
2×2 渐开矩阵示例:
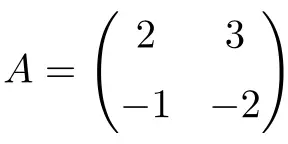
我们可以通过计算矩阵的二次方来验证它是一个对合矩阵:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-314aebadfe3da501264c0eb14e1dfc2f_l3.png)
由于矩阵 A 的平方是单位矩阵,因此矩阵 A 是 2×2 的对合矩阵。
3×3 渐开矩阵示例:
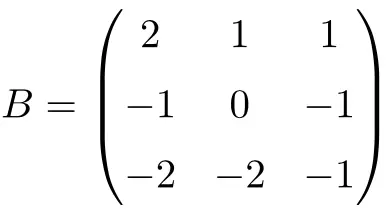
我们可以通过求解矩阵的乘积来验证它是一个对合矩阵:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599241f00e8a89f8b55ed2ae8cb42ddb_l3.png)
由于矩阵 B 的平方是单位矩阵,因此矩阵 B 是 3×3 的对合矩阵。
4×4 渐开矩阵示例:
单位(或单位)矩阵,无论其维度如何,根据定义都是对合矩阵。
![Rendered by QuickLaTeX.com \displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4278c2b46761d3b258eb9ba04c87bbf1_l3.png)
我们可以通过将矩阵提高到 2 来验证它是一个对合矩阵:
![Rendered by QuickLaTeX.com \displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3190f24d196c4b96a60ec06fe7180e6_l3.png)
由于单位矩阵的平方是单位矩阵,单位矩阵是一个4×4的对合矩阵。
显然,单位矩阵可以是任何维度,因为它只是一个主对角线上全 1 且其余部分为 0 的对角矩阵。因此,无论阶数如何,单位矩阵始终是一个对合矩阵。
求和矩阵公式
卷积矩阵的性质之一是它的公式是已知的。但是二阶对合矩阵公式的证明相当乏味,所以我们直接看结果,这才是真正重要的。如果您对演示更感兴趣,可以在下面的评论中看到它的逐步解释。
维度为 2 × 2 的对合矩阵的公式如下:

因此,任何主对角线值相反且行列式为-1的矩阵,都将是对合矩阵。
然而,除了这个公式描述的矩阵之外,还必须考虑到单位矩阵及其相反也是2阶对合矩阵:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-395beb5a766a10eefa56a087e8c8d098_l3.png)
渐开矩阵的性质
卷积矩阵具有以下特点:
- 卷积矩阵的行列式总是等于-1或+1。
- 卷积矩阵和幂等矩阵之间存在关系:矩阵

是对合的当且仅当矩阵
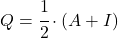
是幂等的。
- 是的

和

是两个可交换的对合矩阵,则矩阵乘积
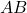
也是另一个对合矩阵。
- 一个对合矩阵的任何幂都会产生另一个对合矩阵。特别是,对合矩阵提高到奇数指数将等于其自身,另一方面,如果它提高到偶数指数,它将等于单位矩阵。
![]()
![]()