本页解释了什么是函数转换以及如何找到它们。变换分为三种类型：平移（或位移）、对称和扩展（或收缩）。您还会发现逐步解决的练习，以便您可以毫无疑问地练习和理解概念。
什么是函数变换？
有时，我们可能会被要求绘制与我们已知的其他函数非常相似的基本函数的图表。那么，不必再次表示相似的函数，而是可以使用技术轻松快速地从表示一个函数切换到另一个函数。
因此，函数变换是一种技术，可以通过初等运算从一个函数的图形表示转移到另一个非常相似的函数的图形表示。
基本上，初等函数的变换分为三种类型：
- 平移或移动：功能可以垂直和水平移动。
- 反射或对称：可以使用 X 轴或 Y 轴作为对称轴来反射函数。
- 扩展和压缩：函数可以被放大或缩小。
一旦我们了解了转换函数的概念，我们将更深入地研究每种类型的修改。
功能的翻译或移动
我们将从功能转变开始。有两种类型：垂直翻译和水平翻译。
函数的平移或垂直移动
要垂直平移或移动函数（沿 Y 轴），必须为函数添加或减去一个常量：
我们通过将 ka 添加到函数中来将函数向上移动 k 个单位：
我们通过从函数中减去ka 将函数向下移动 k 个单位：
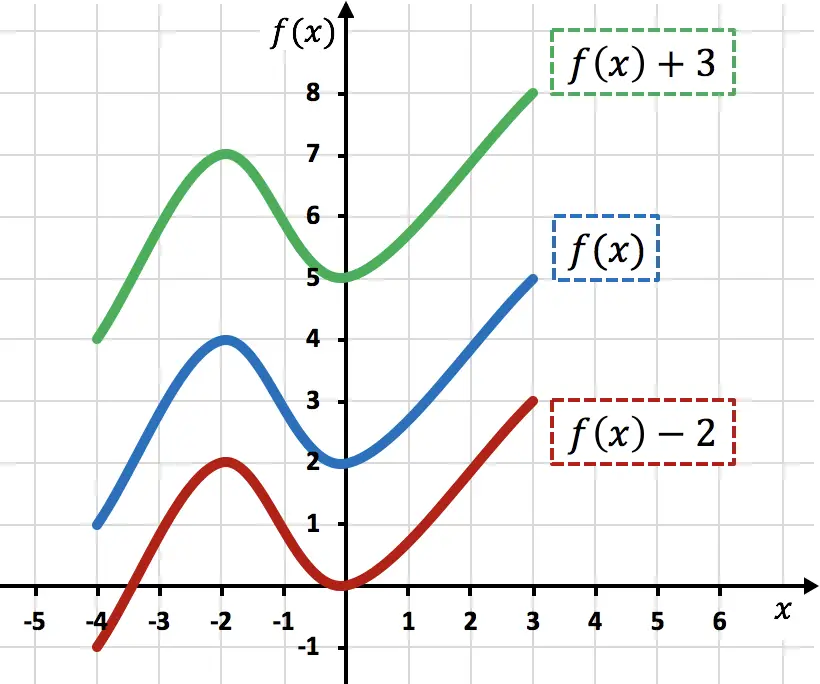
从图中可以看出，向任何函数添加常量都会向上移动添加的单位（绿色函数）。另一方面，当从函数中减去数字时，减去的单位会向下移动（红色函数）。
请注意，在这种类型的运动中，仅功能点的 Y 坐标发生变化，而 X 坐标保持不变。
功能的平移或水平移动
要水平平移或移动函数（沿 X 轴），您必须为自变量x添加或减去一个常数：
的图表
是的图
向左移动 k 个单位。
的图表
是的图
向右移动 k 个单位。
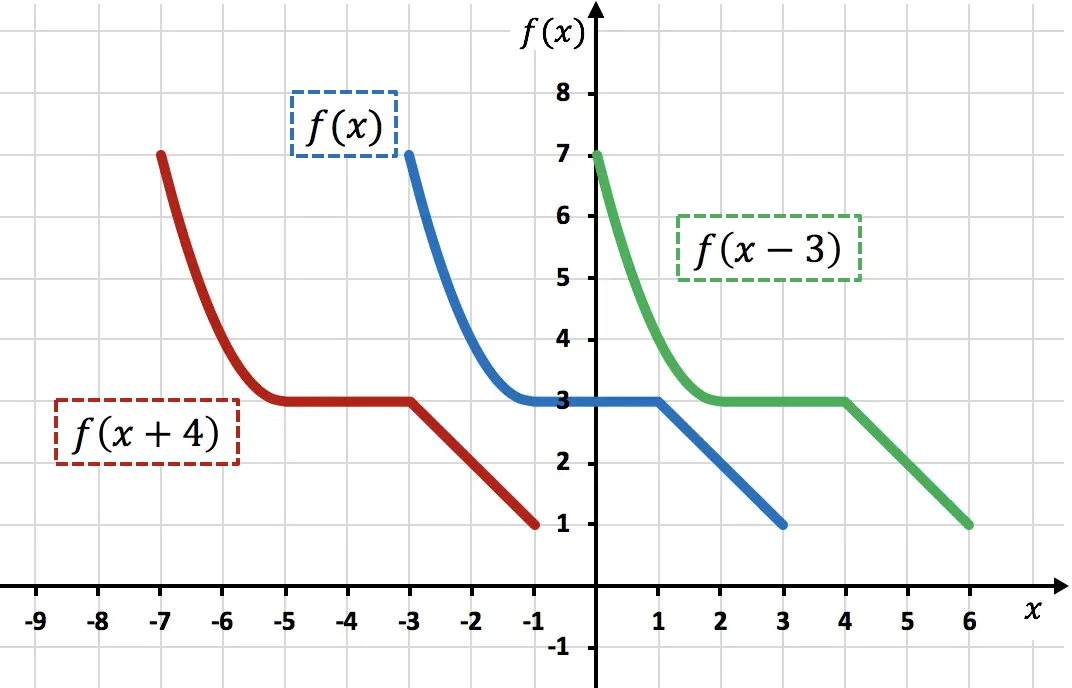
从图中可以看出，当直接向变量x添加常量时，该函数会将添加的单位向左移动（红色函数）。另一方面，当从变量x中减去一个数字时，该函数将减去的单位向右移动（绿色函数）。
请注意，在这种类型的运动中，仅改变功能点的 X 坐标，而 Y 坐标继续保持相同的值。
平移或移动函数的示例
- 将以下函数向上移动 4 个单位，向右移动 3 个单位：
要将函数向上移动 4 个单位，我们需要向函数添加 4 个单位：
为了将函数向右移动 3 个单位，我们必须计算
。因此，凡是有一个
我们可以
因此，函数向上移动 4 个单位并向右移动 3 个单位为：
下面绘制了原始函数和转换后的函数，以便您可以看到它们之间的区别：
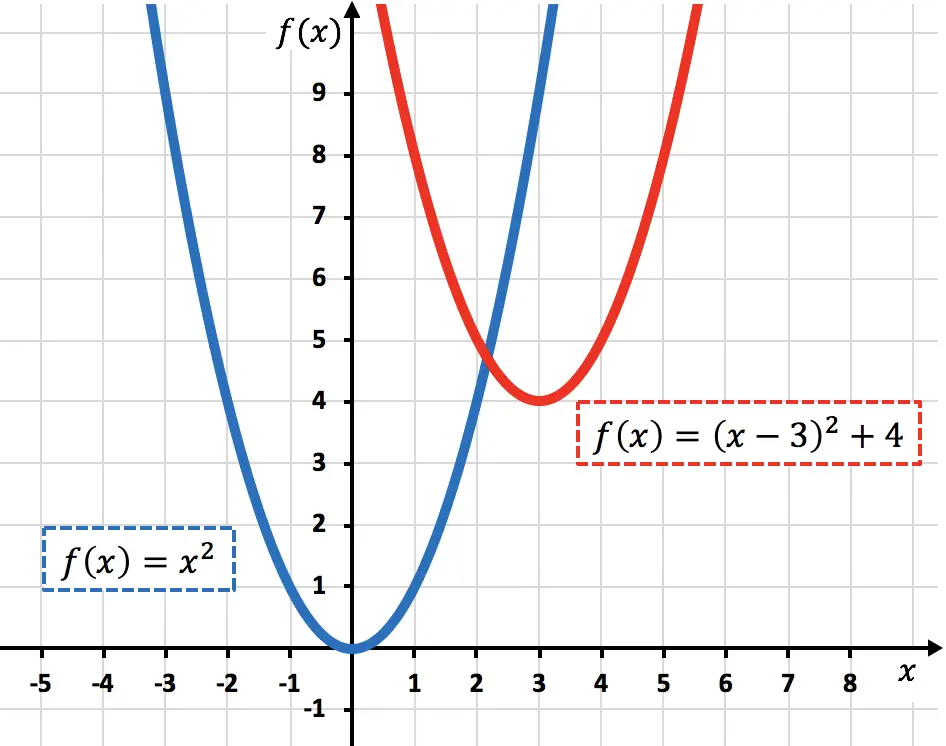
当两种类型的运动同时发生时，一些数学家将其称为倾斜位移或平移。
函数相对于坐标轴的反射或对称
我们可以用以下方式表示关于任何笛卡尔轴的对称函数：
为了反映一个函数相对于x轴的情况，我们需要改变函数的符号，也就是说，我们需要计算
为了反映关于 y 轴的函数，我们必须对自变量x求反，也就是说，我们必须计算
正如您在上图中看到的，通过将函数乘以 -1，我们以图形方式反转它（橙色函数），或者换句话说，我们相对于 X 轴镜像它。
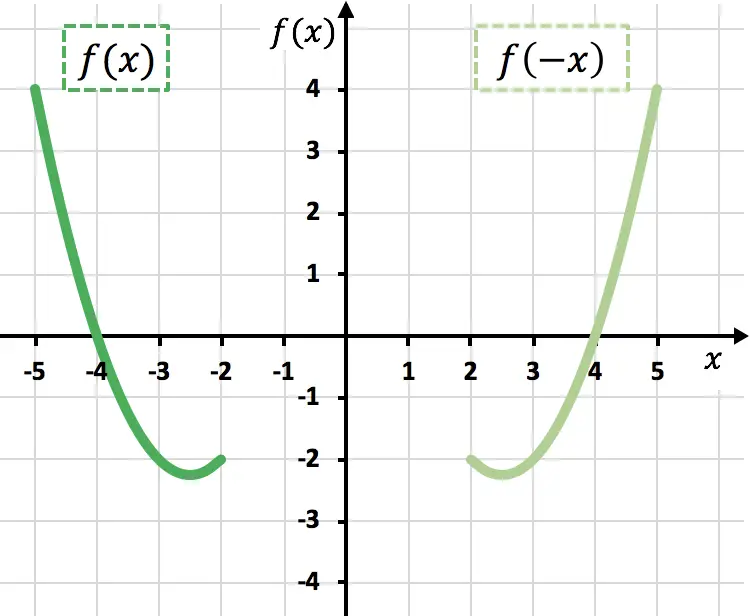
从上图中可以看出，通过否定变量x ，我们相对于 Y 轴镜像函数（浅绿色函数）。
镜像函数的示例
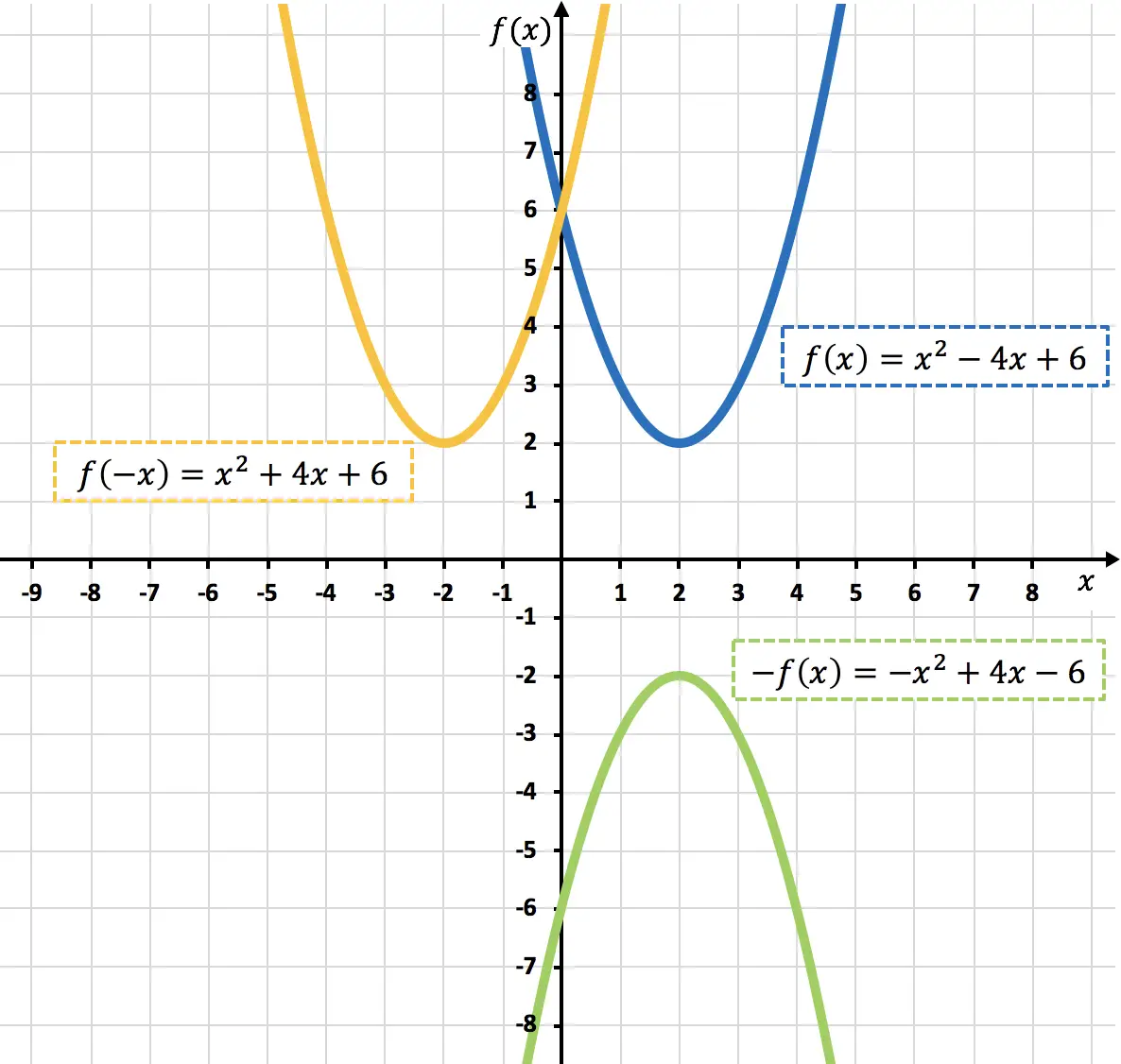
- 计算以下二次函数的关于 OX 轴的对称函数和关于 OY 轴的对称函数：
要找到关于 X 轴对称的函数，我们必须这样做
：
![-f(x)=-\bigl[x^2-4x+6\bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec1ca457c73589ee30ad6641f0d66c10_l3.png "Rendered by QuickLaTeX.com")
为了找到关于 Y 轴对称的函数，我们必须这样做
。因此，我们将存在的地方替换为
在原函数中由术语
下面你展示了原始函数和找到的对称函数：
函数的扩展和收缩
与翻译一样，有两种类型的扩展或收缩：垂直和水平。
函数的垂直扩展和收缩
通过将整数函数乘以系数，我们可以使其扩展或收缩：
要在 Y 轴上扩展（或膨胀）函数，我们需要将其乘以大于 1 的数字：
要减少 Y 轴上的函数，我们需要将其乘以小于 1 的正数：
要减少 X 轴上的函数，我们需要将所有x乘以大于 1 的数字：
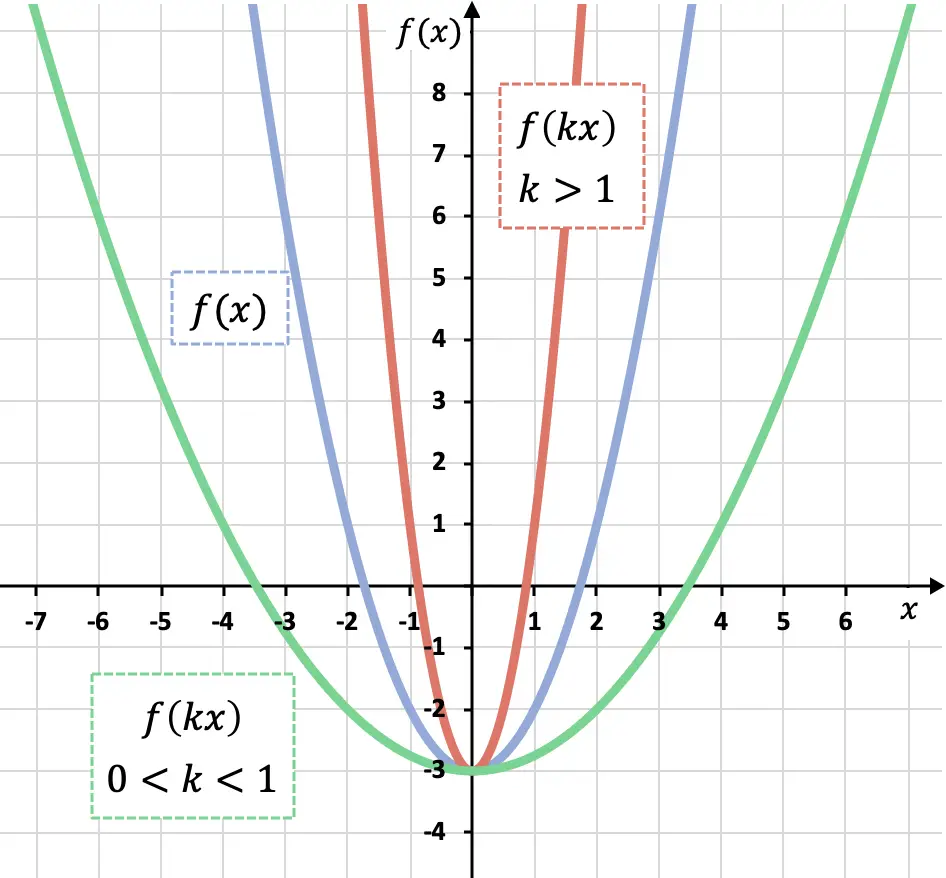
正如您在上图中看到的，如果我们将函数的所有x乘以大于 0 但小于 1 的系数（绿色函数），我们就会沿 OX 轴放大它，另一方面，如果我们乘以一个系数大于 1 的函数（红色函数），我们沿 OX 轴减少它。
如何展开或折叠函数的示例
- 垂直和水平复制以下无理函数：
要将函数在 y 轴上扩展 2，我们必须将整个函数乘以 2：
并且为了在 x 轴上将函数扩展为 2，我们必须将函数的所有x乘以
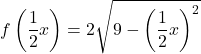
因此，在两个坐标轴上复制的函数为：
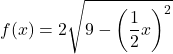
下面以图形方式显示原始函数和转换后的函数，以便您可以看到它们之间的差异：
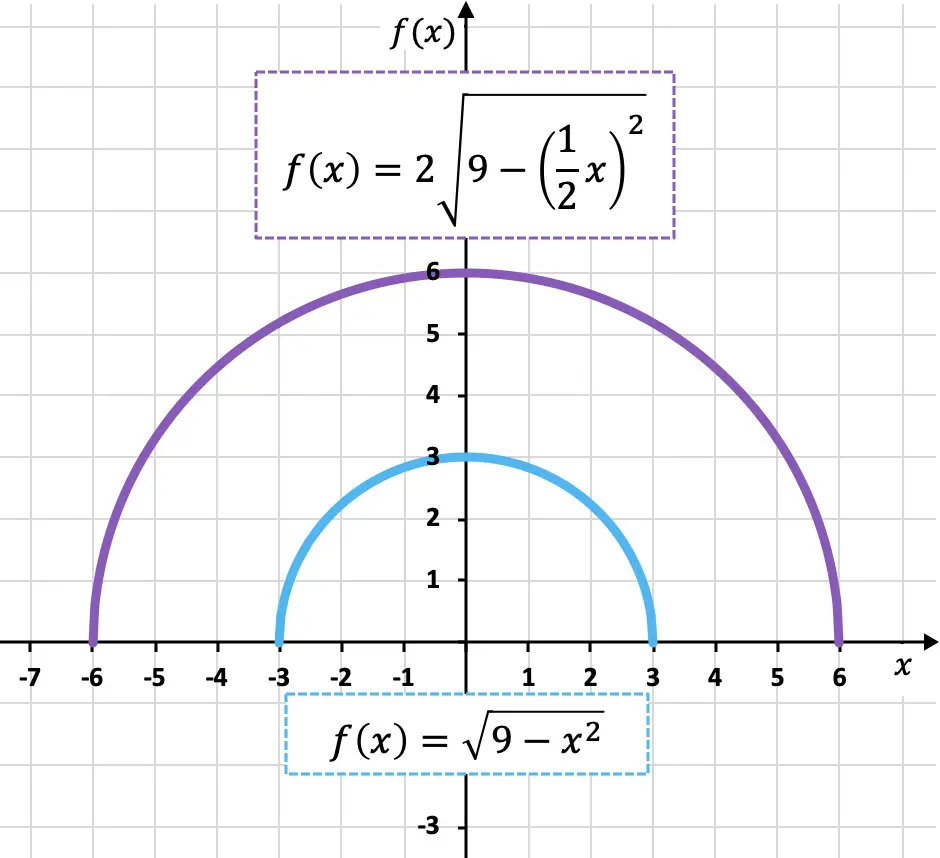
正如您所看到的，新特征（紫色）在垂直和水平方向上都是原始特征（蓝色）的两倍，因此，该特征已扩展。
解决了函数转换的练习
练习1
将下列三次函数上移 5 个单位：
要将函数向上移动 5 个单位，请向函数添加 5：
![\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png "Rendered by QuickLaTeX.com")
因此，移动 5 个单位的函数为：
练习2
求以下二次函数关于 Y 轴的对称函数：
为了找到关于 Y 轴对称的函数，需要计算
，也就是说，我们需要替换
为了
在函数中：
因此，相对于 OY 轴的对称函数为：
练习3
将以下函数执行水平压缩至其表示的三分之一：
通过以下方式减少函数
因此，简化后的函数为：
练习4
计算以下函数相对于 OX 轴向右平移 4 个单位的对称函数：
在计算对称函数之前，我们必须先将函数向右移动4个单位，因此：
一旦我们移动了函数，我们就计算相对于 X 轴的对称函数。为此，我们必须对所获得的函数求反：
![\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-62a7ea0e19503ec030dcdaa59c9157eb_l3.png "Rendered by QuickLaTeX.com")
简而言之，应用所有初等运算后的函数是：
练习5
将以下函数向左移动 2 个单位，然后将其垂直展开 4 倍：
首先，我们将函数向左移动两个单位：
然后我们将函数沿 Y 轴展开 4 倍：
![4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-07175c64db9d7e8074852df8944df6c4_l3.png "Rendered by QuickLaTeX.com")
总之，应用所有初等变换后的函数为：
练习6
从函数来看
确定图表上的哪个表示对应于该函数
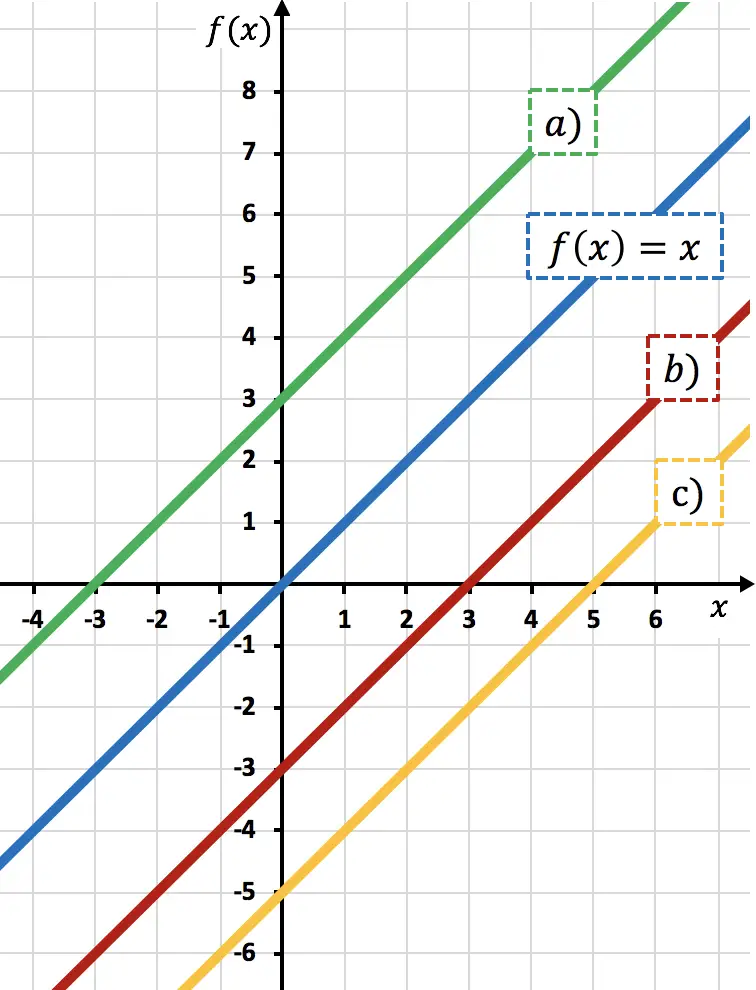
功能
是函数
向下移动了 3 个单位。因为通过从函数中减去一个数字，您可以将函数向下移动。
因此，代表
对应于线 b) ，因为与线相比，它向下移动了 3 个单位
这可以通过观察纵轴看出：
穿过 0，红线穿过 -3，因此向下移动 3 个单位。
练习7
从函数来看
确定哪个抛物线是函数的表示
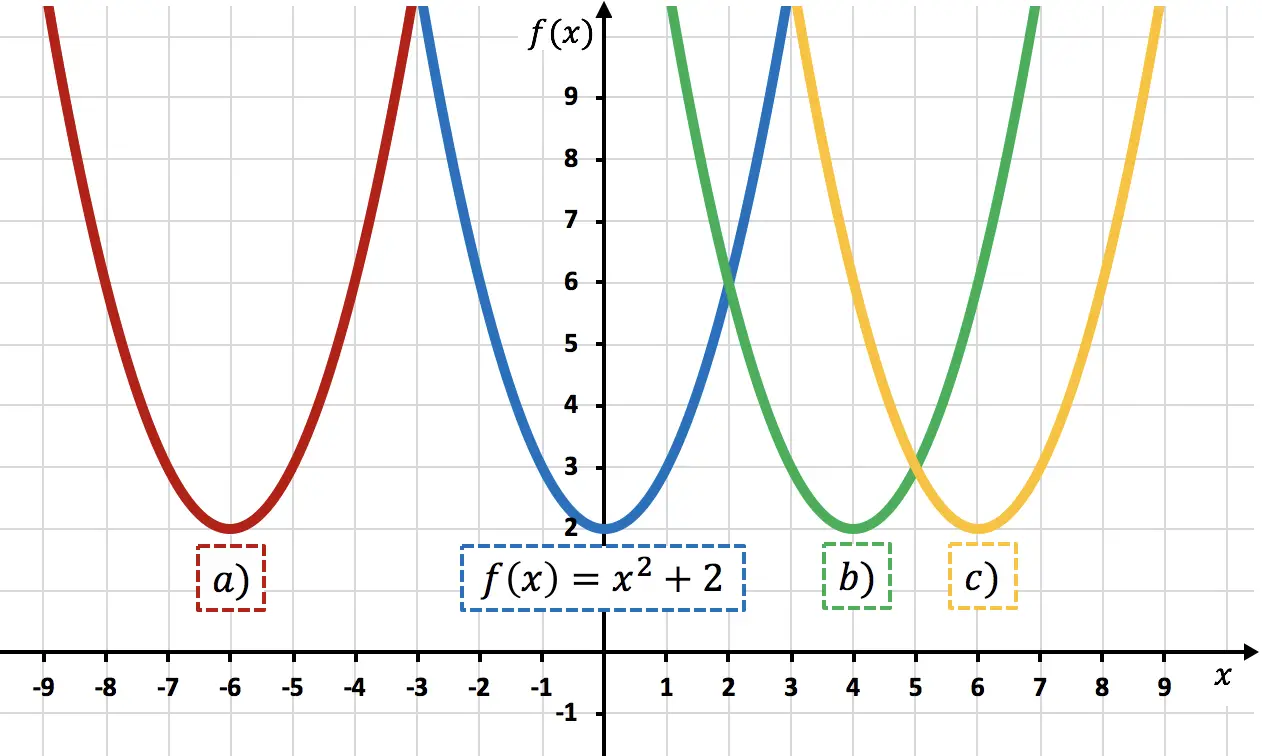
功能
是函数
向右移动了 6 个单位。我们可以通过计算来验证这一点
因此，代表
对应于抛物线 c) ，因为与
。
这可以通过观察抛物线的顶点来看出：抛物线顶点之间的距离
抛物线c)的顶点为6个单位，因此后者比第一个抛物线向右移动了6个单位。