单项式 - 数学

在这里，我们解释了您需要了解的有关单项式的所有信息：它们是什么、它们的组成部分是什么（以及如何识别它们）、单项式的不同类型、如何使用单项式计算运算、单项式的数值。 .. 此外，您将能够看到逐步解决单项式的示例和练习。

什么是单项式？

在数学中，单项式的定义如下：

单项式是由数字和字母组合形成的代数表达式。更准确地说，单项式由一个数字和一个或多个指数变量（字母）之间的乘积组成。

例如，术语 7x ³ y ²称为单项式，因为它有一个数字 (7) 和不同的字母 (x, y)。

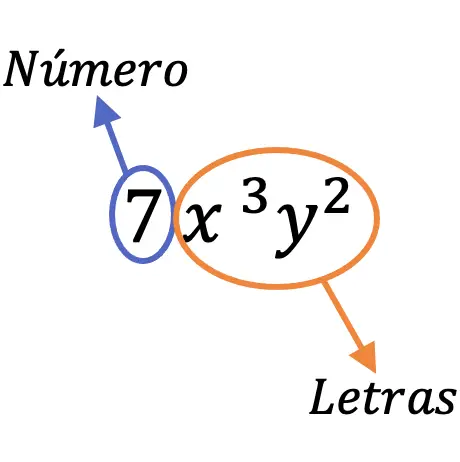
单项式的部分

现在我们已经了解了单项式的含义，让我们看看单项式的所有部分是什么：

系数：是单项式的变量（或字母）相乘的数字。
变量：是单项式中出现的每个字母。
文字部分：对应于构成单项式的所有变量及其各自的指数。
度数：由构成单项式的字母的所有指数之和组成。

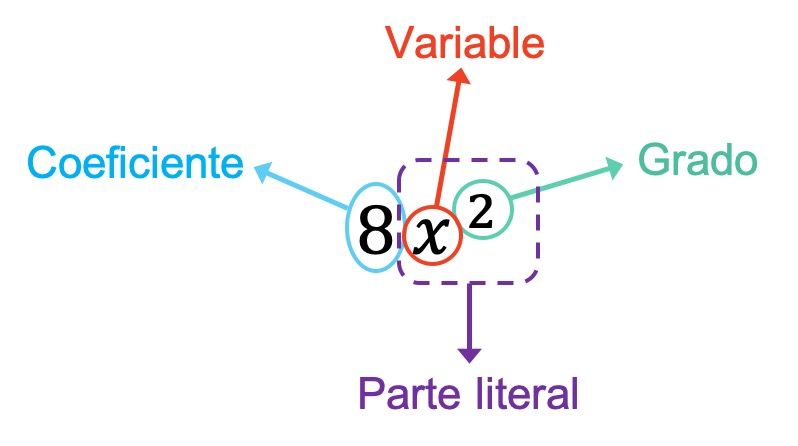
上例中单项式的系数为 8，因为它是与变量相乘的数字。此外，在这种情况下，单项式只有一个变量，即 x。因此，单项式的文字部分由该变量加上其指数（即 x ^{2 ）}组成。最后，单项式的次数为 2，因为它是它唯一的指数。

现在尝试解决单项式各部分的以下练习：

识别下列单项式的所有部分：

$5x^4y^2z$

查看解决方案

该陈述的单项式的组成部分是：

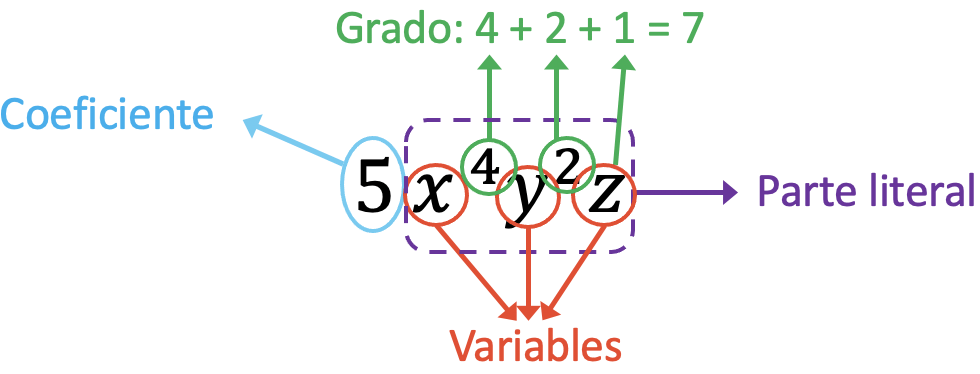
问题中单项式的系数是 5，因为它是与字母相乘的项。另一方面，该单项式的变量是 x、y、z。第三，单项式的文字部分对应于表达式 x ⁴ y ² z。最后，单项式的次数等于变量所有指数的总和，即7 (4+2+1=7)。

请注意，当一个字母没有指数时，实际上意味着它的指数为 1。因此，为了计算问题的单项式次数，我们添加一个表示变量 z 的指数的单位。

单项式的类型

单项式有不同类型，每种类型都有自己的属性。最重要的单项式是相似单项式、同质单项式、异质单项式和相反单项式。接下来我们将看到每种类型的特征。

相似的单项式

相似单项式是具有相同字面部分的单项式。因此，当两个或多个单项式具有相同的字母和指数时，它们是相似的。

例如，以下两个单项式是相似的，因为尽管它们具有不同的系数，但它们由相同的变量形成并提升到相同的指数。

$4x^5y^3 \qquad \qquad 9x^5y^3$

正如我们稍后将看到的，这种类型的单项式用于求解单项式的运算。

齐次单项式

当两个单项式的绝对次数相等时，它们是齐次的。

例如，以下两个单项式是齐次的，因为两者的次数都等于 5：

$2x^5 \qquad \qquad 6x^2y^3$

第一个单项式有一个变量的 5 次方，因此其次数为 5。第二个多项式有一个变量的平方和另一个变量的立方，因此其次数也是 5 (2+ 3 =5)。

正如您所看到的，要使两个单项式齐次，它们不需要具有相同的文字部分，而只需具有相同的绝对次数即可。

异质单项式

异质单项式是不具有相同绝对次数的单项式。换句话说，异质单项式与同质单项式相反。

以下 3 个单项式是异质的，因为每个单项式的次数不同：

$x^8 \qquad 3xy \qquad 7a^9b^2$

第一个单项式的次数为 8，第二个单项式的次数为 2，第三个单项式的次数为 11。因此，这三个单项式彼此异质。

相反的单项式

相反单项式是齐次（具有相同文字部分）的单项式，而且它们的系数相反，即它们的系数具有相同的值但符号相反。

例如，以下两个单项式是相反的：

$3x^5y^2 \qquad \qquad -3x^5y^2$

前面的两个单项式是相反的，因为它们仅在符号上不同，第一个有正号，第二个有负号。

现在您已经看到了单项式的几个示例，您可能对另一个类似的代数表达式感兴趣：二项式。事实上，二项式是由几个单项式相加（或相减）组成的，因此了解这两个概念之间的关系很有趣。您可以通过单击此链接了解二项式的含义。

单项式运算

为了加深单项式的概念，我们将看看单项式可以进行哪些运算。特别是，单项式可以进行加、减、乘、除和幂运算。而且每种操作都有其特殊性，下面我们就分别一一分析。

单项式总和

两个或多个单项式只有在相似单项式时才能相加。那么，两个相似单项式的和等于由相同文字部分组成的另一个单项式以及这两个单项式的系数之和。

单项式和的示例

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

如果你想练习做单项式加法练习，你可以在右上角的搜索引擎中搜索它们，因为我们有一整页都是已解决的单项式加法练习。

单项式减法

两个或多个单项式只有在相似单项式时才能相减。因此，两个相似的单项式相减等于由相同文字部分组成的另一个单项式与这两个单项式的系数相减。

单项式相减的例子

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

您可以通过我们网站上找到的已解决的单项减法练习进行练习。您可以通过右上角的搜索引擎找到它们。

单项式的乘法

两个单项式相乘的结果是另一个单项式，其系数是单项式系数的乘积，其文字部分是通过将具有相同基数的变量相乘（即通过将它们的展示者相加）获得的。

因此，要求解两个不同单项式之间的乘积，必须将系数相乘，并且必须将具有相同底数的幂的指数相加。

另一方面，如果我们将两个具有不同基幂的单项式相乘，我们只需将它们的系数相乘并保持幂相同：

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

单项式乘法的例子

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

要练习单项式乘法的分步练习，您可以查阅我们在本网站上提供的文章。您可以通过右上角的搜索引擎轻松找到它。

单项式除法

单项式除法的结果是另一个单项式，其系数等于单项式系数的商，其文字部分是通过将具有相同基数的变量相除（即减去它们的展示者）获得的。

因此，要除以两个不同的单项式，我们只需将它们之间的系数相除，然后减去具有相同底数的幂的指数即可。

单项式除法的例子

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

单项式除法比看起来更困难，因此我们建议您尝试逐步完成我们关于单项式除法的练习。找到它们的最快方法是通过我们右上角的搜索引擎。

单项式的幂

要计算单项式的幂，必须将单项式的每个元素求幂指数。换句话说，单项式的幂包括将其系数及其变量（字母）提高到幂的指数。

请记住，根据幂的性质，当我们提出一个已经提出的项时，两个指数会相乘。因此，在单项式的幂中，每个字母的指数总是乘以表示幂的指数。

单项式幂的示例

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$