单位或矩阵单位

在此页面上，您将看到单位（或单位）矩阵是什么以及几个示例。此外，我们还解释了单位矩阵的属性是什么、如何使用这种类型的矩阵以及其行列式的结果是什么。最后，您将发现这个非常特殊的矩阵的应用。

什么是单位矩阵？

单位（或单位）矩阵是一个用零 (0) 填充的方阵，但主对角线上的所有元素均为一 (1)。

这是单位矩阵或单位矩阵的定义，但是通过示例你一定会更清楚地看到它：

单位矩阵的示例

维度为 2 × 2 的单位矩阵示例

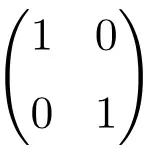
3×3 阶单位矩阵示例

大小为 4×4 的单位矩阵示例

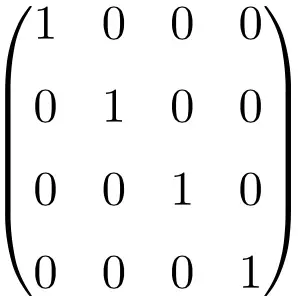
正如您所看到的，要构造单位矩阵，我们仍然需要遵循相同的过程：将 1 放在主对角线上，其余全为零 (0)。唯一改变的是表格的大小。

身份表属性

单位矩阵、单位矩阵甚至同矩阵在数学中被广泛使用，这是由于此类矩阵所具有的特性：

单位矩阵是对角矩阵的一个例子。

酉矩阵既是上三角矩阵又是下三角矩阵。

单位矩阵也是对称矩阵。

单位矩阵的副手就是它本身。

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

它是一个可逆矩阵。并且，对于伴随来说，单位矩阵的逆就是它本身：

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

任何标量矩阵都可以通过将数字乘以单位矩阵来获得：

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Identical 矩阵的所有特征值（或特征值）均为 1：

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

最后，单位矩阵也是置换矩阵的一个例子。

单位（或单位）矩阵的运算

您可能在想：这一切都很好，但是……单位矩阵有什么用？如果这是一张有 0 和 1 的表就好了！

虽然你可能还没有给出这个话题，但单位矩阵在数学中被大量使用，事实上，这种类型的方阵在线性代数中非常重要。单位矩阵的主要用途是它可以轻松地进行矩阵运算的计算。让我们看看如何使用单位矩阵：

使用单位矩阵进行加法和减法

在不更改其他元素的情况下在矩阵主对角线上添加（或减去）数字的一种方法是使用单位矩阵，因为它仅向这些数字添加（或减去）一个单位。要素：

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

您还可以通过首先将单位矩阵乘以标量来向对角线上的元素添加或减去更多单位：

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

矩阵乘以单位矩阵

将矩阵与单位矩阵相乘时，它充当中性元素，即任何矩阵与单位矩阵相乘都会得到相同的矩阵。看一下下面的例子：

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

此外，矩阵乘积的含义是无关紧要的，或者换句话说，我们将单位矩阵右乘还是左乘并不重要，因为结果总是相同的矩阵。为了证明这一点，我们重复之前的练习，但这次将单位矩阵乘以相反的一侧：

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

单位矩阵的幂

无论矩阵的指数和矩阵的维数如何，单位矩阵的幂始终会产生单位矩阵。

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

单位矩阵的行列式

正如我假设您已经想象的那样，单位（或单位）矩阵的行列式始终等于 1 ，无论矩阵的维度如何。

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

单位矩阵应用

最后，了解所有这些信息后，您可能已经知道如何回答为什么单位矩阵如此重要的典型问题？放松，我以前也问过自己这个问题。 😂

正如您所注意到的，单位矩阵有很多用途，这就是它如此有趣的原因。单位矩阵的用途之一是运算，因为正如我们所见，用它执行矩阵运算非常容易。

另一方面，单位矩阵也用于求解矩阵方程。为此，我们使用以下逆矩阵属性：将一个矩阵与其逆矩阵相乘等于单位矩阵。您可以通过单击链接了解如何用矩阵求解方程。

另外，单位矩阵还用于用高斯方法计算逆矩阵。该方法涉及在单位矩阵旁边放置一个矩阵，从而形成一个更大的矩阵。然后，必须通过对行应用初等运算将原始矩阵转换为单位矩阵。看起来很复杂，但实际上并没有那么复杂，但是必须应用整个过程，所以如果您更感兴趣，您可以在网页的搜索引擎中搜索如何反转矩阵（从上到右）。

最后，单位矩阵对于对角化矩阵并计算其特征值（或多个特征值）也很有用。因为通过一定的运算，其中单位矩阵介入，就可以得到得到特征值的特征多项式。但这已经是一个非常高级的主题，这就是为什么我们有一个完整的超级综合页面专门用于矩阵对角化，其中包含示例和解决的练习来解释它。如果您更感兴趣，可以在我们的搜索引擎（右上角）中搜索本指南。