在这里,我们解释如何导出幂(或势函数),您将找到幂导数的公式,几个示例,您甚至可以通过逐步解决的练习进行练习。
幂的导数公式
幂或势函数的导数是幂的指数乘以底数的指数减去 1 乘以底数的导数的乘积。
![]()
因此,如果基数是恒等函数,要得到幂,只需将函数乘以指数,然后从指数中减去一个单位:
![]()
事实上,恒等函数的导数等于 1。
总之,要导出势函数,有两个公式:第一个公式始终可用,第二个公式仅当底为 x 时才适用。
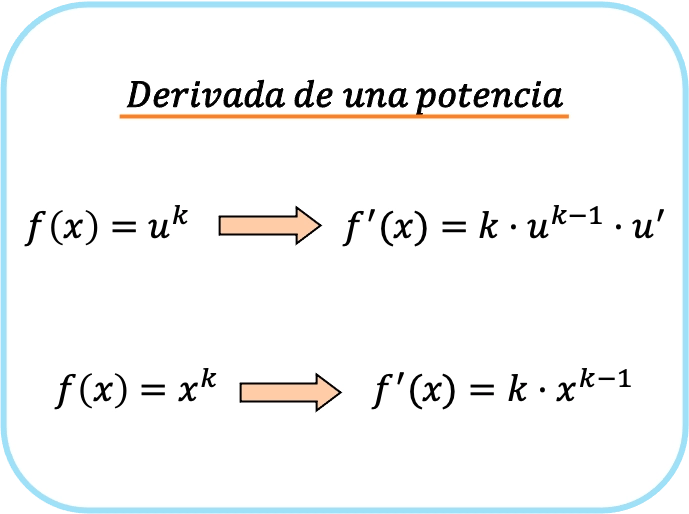
我们可以轻松验证幂导数的第一个公式与第二个公式相似,但应用了链式法则。
请注意,这些公式仅当变量是幂的底数时才能使用,如果 x 位于分母中,则必须应用指数函数导数的规则:
➤请参阅:指数函数的导数
幂导数的例子
一旦我们了解了势函数的导数公式,我们将解释此类导数的几个示例,以便您了解幂是如何导出的。
示例 1:基数 x 的导数
![]()
正如我们在上一节中所解释的,当幂的底数仅为 x 时,我们必须使用以下公式来推导该函数:
![]()
因此,x 次方 4 次方的导数为:
![]()
示例 2:带括号的幂的导数
![]()
在这个例子中,基数不是恒等函数,因此我们必须使用幂导数的通用公式:
![]()
括号中的函数是线性函数,因此它的导数为2。因此,整个势函数的导数为:
![]()
示例 3:负幂的导数
![]()
在这种情况下,我们有一个指数为负且底数为对数的势函数,因此我们将使用以下公式对该函数进行微分:
![]()
即使幂指数为负数,也必须减一。因此该函数的导数为:
![]()
如果您对解法有任何疑问,可以在这里查阅对数函数导数的公式:
➤请参阅: 对数函数的导数
示例 4:带根的幂的导数
![]()
此示例中的函数是正则表达式中的幂。然而,根式可以转换为势表达式,因此可以通过将其转换为带有分数指数的势函数来简化该函数:
![]()
现在我们应用变量幂的导数公式:
![]()
导数为:
![]()
您还可以使用根导数规则区分这些类型的函数:
➤请参见: 源自根
解答了幂导数的练习
计算以下幂的导数:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
查看解决方案
![]()
![]()
![]()
![]()
![]()
![]()
![]()
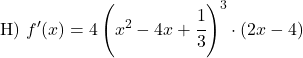
![]()