在这里您将了解正切函数是如何导出的。此外,您将能够看到切线导数的示例,甚至可以通过逐步解决的练习进行练习。最后,我们还演示了正切导数公式并向您展示反正切导数公式。
切线的导数是什么?
x 的正切值对 x 的余弦平方的导数等于 1。 x 的正切的导数也等于 x 的正割的平方,1 加上 x 的正切的平方。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfb81626a982a908c4e517b1ecb748e7_l3.png)
所有表达式都是等价的,因此正切函数具有三个可能的公式来导出它。
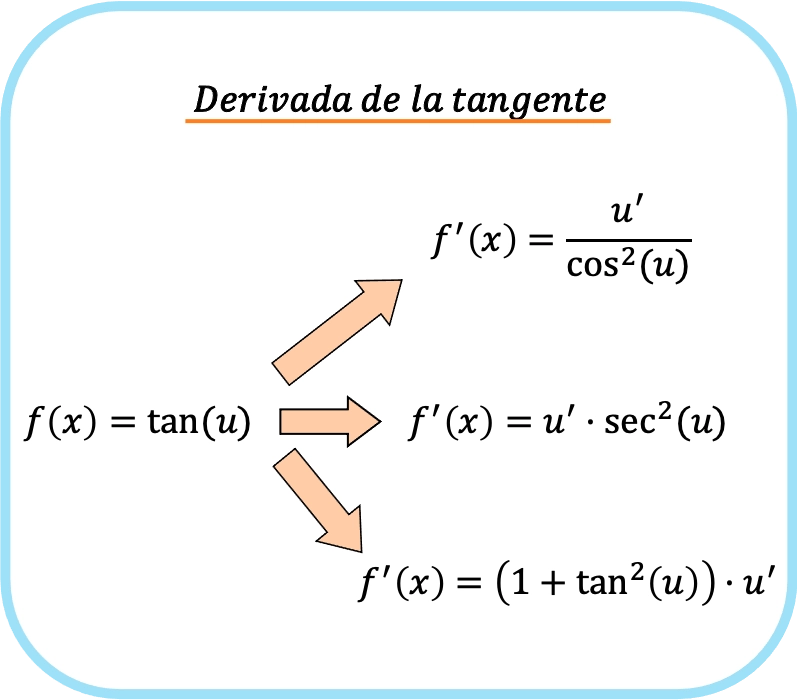
另一方面,当在正切参数中我们有一个与 x 不同的函数(我们称之为 u)时,我们必须应用链式法则。因此 u 的正切导数为:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ad272ab857ecf57ebc79e68a4370fc5_l3.png)
简而言之,正切导数规则可以概括为:
正切导数的例子
给定正切导数的公式,在本节中,我们将求解此类三角导数的几个示例,以便您了解如何推导正切函数。
示例 1:2x 的正切的导数
![]()
要计算正切的导数,您可以使用我们上面看到的三个公式之一。在这种情况下,我们将使用余弦公式:
![]()
函数 2x 是线性的,因此它的导数为 2。因此 2x 的正切对 2x 余弦平方的导数为 2:
![]()
示例 2:x 平方正切的导数
![]()
在此示例中,正切参数函数不是 x,而是具有导数的函数。这意味着我们需要应用链式法则来推导它。
![]()
x 平方的导数为 2x,因此 x 2的正切的导数为:
![]()
示例 3:立方体切线的导数
![]()
在这个问题中,我们有一个复合函数,因此我们还需要使用链式法则来微分切线。
![]()
此外,正切是 3 次方,这意味着在应用正切导数公式之前必须使用幂导数公式:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-424a7372a1d97a5c17a86d6253666164_l3.png)
反正切的导数
与任何反函数一样,正切函数也有一个反函数,即反正切函数。尽管导出它的公式与正切公式并不相似,但我们向您展示它是因为它在某些情况下很有用。
函数反正切的导数是函数的导数除以一加上该函数的平方所得的商
![]()
例如,3x 的反正切的导数为:
![]()
解决了切线导数的练习
计算以下正切函数的导数:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
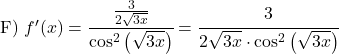
正切导数的证明
为了验证这不是一个虚构的表达式,在本节中我们将使用正切的数学定义来演示正切导数的公式。
为此,我们将从连接三个三角比率的三角恒等式开始:
![]()
如果我们使用除法的导数公式,导数将是:
![]()
![]()
![]()
但是,使用基本三角恒等式,我们知道正弦的平方加上余弦的平方是 1:
![]()
![]()
这样我们就得到了第一个正切导数公式。而且,正割是余弦的乘法逆元,因此也推导出第二个表达式:
![]()
最后,正切导数的第三条规则可以通过将上一步的分数转化为分数和来证明:
![]()
![]()
![]()