函数运算：加法、减法、乘积、除法和合成

17 9 月, 2023

在本文中，我们将解释可以使用函数执行哪些操作。您将能够看到有关函数运算的解释以及已解决的练习。最后，您将找到函数操作的属性。

什么是函数运算？

您可以使用函数执行 5 种不同类型的运算：加法、减法、乘积、除法和合成。也就是说，两个函数可以相加、相减、相乘、相除或组合。

接下来，我们将了解每种类型的操作是如何进行的、功能以及每种操作的特点。

函数总和

两个函数的总和（或相加）的值等于每个函数的值的总和。换句话说，要计算求和函数的图像，只需将参与运算的函数的图像相加即可。

$(f+g)(x)=f(x)+g(x)$

此外，两个函数之和的域是每个求和函数的域的交集。

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)$

让我们通过一个例子来看看如何添加两个函数：

$f(x)=x^2+1 \qquad g(x)=\log(x-1)$

我们首先添加两个函数：

$(f+g)(x)=f(x)+g(x)=x^2+1+\log(x-1)$

现在我们找到求和函数的域。为此，我们分别计算每个函数的域：

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=(1,+\infty)$

➤请参阅：如何计算函数的域

那么，运算结果的函数域将是：

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)=(1,+\infty)$

每个带有函数的运算都必须附有其域来完整定义结果。

函数减法

两个函数相减（或差）的图像是参与运算的每个函数的图像相减：

$(f-g)(x)=f(x)-g(x)$

与加法函数一样，两个函数的减法域相当于每个函数的域的交集。

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)$

因此，如果在自变量 x 的某个值处未定义函数，则减法所得的函数也不会被定义。

我们通过一个例子来看看两个函数是如何相减的：

$f(x)=\sqrt{x}\qquad g(x)=\cfrac{3}{x-4}$

我们首先将两个函数相减：

$(f-g)(x)=f(x)-g(x)=\sqrt{x}-\cfrac{3}{x-4}$

然后我们确定减法函数的域：

$\text{Dom}(f)=[0,+\infty)\qquad\text{Dom}(g)=\mathbb{R}-\{4\}$

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)=[0,4)\cup (4,+\infty)$

旗舰产品

要计算两个函数的乘积或（乘法） ，您只需将每个函数的表达式相乘即可。

$(f\cdot g)(x)=f(x)\cdot g(x)$

另一方面，乘积函数的域是每个乘法函数的域的交集。

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)$

例如，如果我们有以下两个函数：

$f(x)=\sqrt[3]{x^2-1}\qquad g(x)=\cfrac{2}{3x+6}$

首先我们通过两个函数来进行产品的操作：

$(f\cdot g)(x)=f(x)\cdot g(x)=\sqrt[3]{x^2-1}\cdot\cfrac{2}{3x+6}=\cfrac{2\sqrt[3]{x^2-1}}{3x+6}$

最后，我们找到运算结果的函数域：

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}-\{-2\}$

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)=(-\infty,-2)\cup (-2,+\infty)$

职能分布

两个函数相除（或商）的数值结果对应于以下等式：

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$

然而，两个函数的除域是每个函数的域的交集减去所有 x，这会取消充当除数的函数，因为否则我们将获得不确定性。

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}$

例如，我们将划分以下功能：

$f(x)=5^x \qquad g(x)=x-3$

功能分布如下：

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\cfrac{5^x}{x-3}$

另一方面，每个函数的域分别由所有实数组成

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}$

然而，由于分数的分母中不能有零，因此在结果函数的域中，我们必须删除所有抵消分母的值（x=3）。

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}=\mathbb{R}-\{3\}$

功能组成

函数的复合是最难解决的运算，因为它是最复杂的概念。

函数组合由两个函数的连续应用组成。从代数上来说，两个函数的复合表示如下：

$(g\circ f)(x)=g\Bigl(f(x)\Bigr)$

另一方面，函数的复合域

$(g\circ f)(x)$

相当于函数域内x所有值的集合

$f$

例如

$f(x)$

属于函数域

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

例如，给定以下两个函数：

$f(x)=x^2+1 \qquad g(x)=3x-4$

求复合函数

$f$

其次是

$g$

我们需要替换表达式

$f(x)$

哪里有一个

$x$

在表达中

$g(x):$

$\begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}$

在这种情况下，两个函数的域都完全由实数组成，因此复合函数的域也将由实数组成。

$\text{Dom}(g\circ f)=\mathbb{R}$

正如您所看到的，组合函数并不是一个容易理解的操作。因此，我们建议您练习以下函数组合练习：

➤参见： 已解决的函数组合练习

函数运算的性质

在所有函数运算中，和与积具有以下属性：

关联性：3个或更多函数相加或相乘的顺序无关。

$f(x)+\bigl[g(x)+h(x)\bigr]=\bigl[f(x)+g(x)\bigr]+h(x)$

$f(x)\cdot \bigl[g(x)\cdot h(x)\bigr]=\bigl[f(x)\cdot g(x)\bigr] \cdot h(x)$

交换律：两个函数相加或相乘的顺序不改变结果。

$f(x)+g(x)=g(x)+f(x)$

$f(x)\cdot g(x)=g(x)\cdot f(x)$

中性元：求和运算、乘积运算具有常数中性元函数
$f(x)=0$

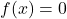
和

$f(x)=1$

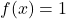
分别。

对称元素：和函数具有相反的函数
$-f(x).$

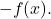
分配性质：该性质将运算的和与积联系起来，并且基于以下等式：

$f(x)\cdot \bigl[g(x)+h(x)\bigr]=f(x)\cdot g(x)+f(x)\cdot h(x)$

发表评论取消回复