函数的拐点 -

这里我们解释什么是函数的拐点以及如何找到函数的所有拐点。此外，您还将找到有关函数曲率和拐点的分步练习。

函数的拐点是什么？

函数的拐点是函数图形曲率发生变化的点，即在拐点处函数从凹变为凸，反之亦然。

如何判断函数是否有拐点

给出了拐点的定义，让我们看看如何知道某个点是否是函数的拐点。

函数在抵消其二阶导数且其三阶导数非零的点处具有拐点。

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

作为示例，我们将计算以下三次函数的拐点：

$f(x)=x^3-5x$

首先，我们计算函数的二阶和三阶导数：

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

现在我们将二阶导数设置为 0 并求解所得方程：

$6x=0$

$x=0$

那么，如果此时的三阶导数不为零，则 x=0 点将是函数的拐点。在我们的例子中，三阶导数始终等于 6。

$f'''(0)=6\neq 0$

因此，x=0 是函数的拐点。

如何研究曲率并找到函数的拐点

我们刚刚看到了一种寻找转折点的方法。然而，我们通常倾向于研究函数的曲率，即确定函数的凹凸，并由此计算拐点。

要通过函数的曲率找到函数的拐点，必须执行以下步骤：

找出不属于函数定义域的点。
计算函数的一阶导数和二阶导数。
求二阶导数的根，即通过求解计算抵消二阶导数的点
$f''(x)=0$

。
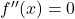
用导数的根和不属于函数定义域的点建立区间。
计算每个区间中某个点的二阶导数值。
二阶导数的符号决定了该区间内函数的凹性或凸性：
- 如果函数的二阶导数为正，则函数在此区间上是凸的。
- 如果函数的二阶导数为负，则函数在此区间上是凹函数。
拐点是函数从凸变为凹或反之亦然的点。

为了让您了解如何使用此过程计算函数的拐点，我们将在下面逐步求解示例：

研究曲率并找到以下多项式函数的拐点：

$f(x)=x^4-6x^2$

首先要做的是计算函数的定义域。它是一个多项式函数，因此函数的定义域由实数组成，也就是说它是一个连续函数：

$\text{Dom } f= \mathbb{R}$

一旦我们计算出了函数的定义域，我们就需要研究函数在哪些点上满足

$f''(x)=0$

。

因此，我们首先计算函数的一阶导数：

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

接下来，我们计算函数的二阶导数：

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

现在我们将二阶导数设置为 0 并求解方程：

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

一旦我们计算了函数的域并且

$f''(x)=0$

，我们表示在数轴上找到的所有临界点：

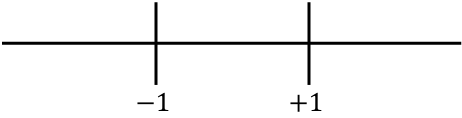
现在我们评估每个区间内的二阶导数的符号，以了解该函数是凹函数还是凸函数。因此，我们在每个区间取一个点（而不是临界点），并查看此时二阶导数的符号：

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

如果二阶导数为正，则表示该函数是凸函数。

$(\bm{\cup})$

，如果二阶导数为负，则意味着该函数是凹函数

$(\bm{\cap})$

。因此，函数的凹凸区间为：

凸面

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

凹

$(\bm{\cap})$

$\bm{(-1,1)}$

此外，在 x=-1 处，函数从凸变为凹，因此x=-1 是函数的拐点。而在x=1时，函数由凹转凸，因此x=1也是函数的拐点。

最后，我们将找到的点代入原函数，求出拐点的Y坐标：

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

因此，函数的转折点为：

转折点：

$\bm{(-1,-5)}$

和

$\bm{(1,-5)}$

下面您可以看到所研究函数的图形表示：

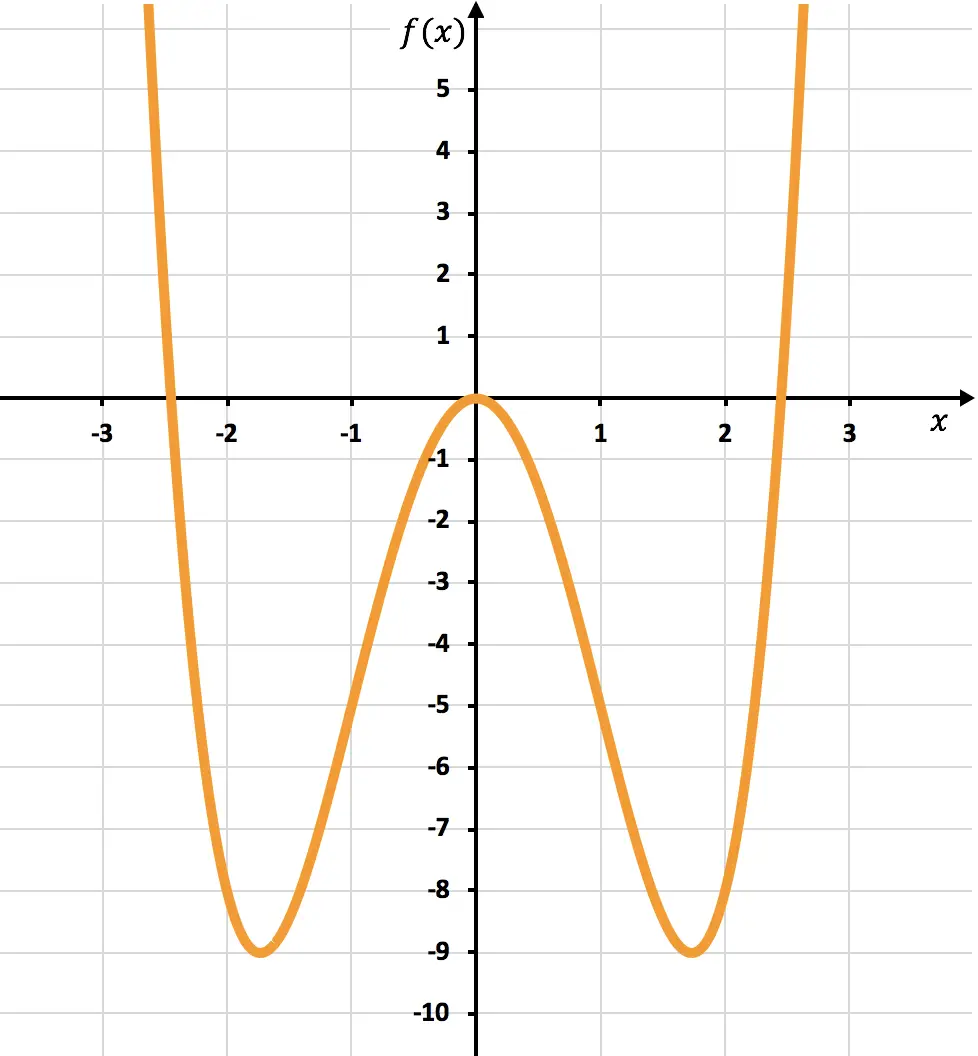
从图中可以看出，该函数从凸函数

$(\cup)$

呈凹形

$(\cap)$

关于

$(-1,-5)$

因为它的曲率发生了变化。另一方面，该函数来自凹函数

$(\cap)$

是凸的

$(\cup)$

关于

$(1,-5)$

。

解决了转弯练习

练习1

计算以下指数函数的凹凸区间以及拐点：

$f(x) = xe^x$

查看解决方案

首先要做的是计算函数的定义域。该函数由多项式函数 (x)（其定义域仅由实数组成）和指数函数 (e ^x )（其定义域也由实数组成）组成。因此，函数的域由实数组成：

$\text{Dom } f= \mathbb{R}$

现在我们来计算函数的导数。在这种情况下，该函数由两个函数的乘积组成，因此要导出该函数，我们需要应用乘积导数的公式：

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

接下来，我们计算函数的二阶导数：

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

我们将二阶导数设置为 0 并求解方程：

$f''(x)= 0$

$2e^x+xe^x= 0$

我们提取公因数：

$e^x(2+x)=0$

为了使乘法等于 0，乘法的两个元素之一必须为零。因此，我们将每个因子设置为0：

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

一个数与另一个数相乘永远不会得到 0。因此，等式

$e^x=0$

没有解决办法。

我们表示右边得到的所有奇异点：

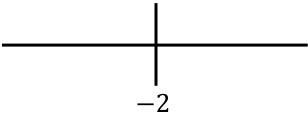
现在我们评估每个区间内的二阶导数的符号来了解该函数是凹函数还是凸函数。为此，我们在每个区间中取一个点，并查看哪个符号在该点具有二阶导数：

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

如果二阶导数为正，则表示该函数是凸函数。

$(\bm{\cup})$

，如果二阶导数为负，则意味着该函数是凹函数

$(\bm{\cap})$

。因此，凹度和凸度区间为：

凸面

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

凹

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

另外，函数在 x=-2 处从凹变为凸，因此x=-2 是函数的拐点。

最后，我们将找到的拐点代入原函数，求出该点的Y坐标：

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

总之，该函数的唯一转折点是：

转折点：

$\bm{(-2,-2e^{-2})}$

练习2

研究凹凸区间并找到以下有理函数的拐点：

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

查看解决方案

首先我们需要计算函数的域。由于这是一个有理函数，我们将分母设置为零，看看哪些数字不属于函数的域：

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

这意味着当x为-2或+2时，分母将为0。因此，该函数将不存在。因此，函数的域由除 x=-2 和 x=+2 之外的所有数字组成。

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

其次，我们计算函数的一阶导数：

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

然后我们求解二阶导数：

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

所有项均乘以

$(x^2-4)$

。因此我们可以简化分数：

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

现在我们来计算函数二阶导数的根：

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

期限

$\left(x^2-4\right)^3$

这涉及到将整个左侧除，因此我们可以将其乘以整个右侧：

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

我们提取公因数：

$x(8x^2+96)=0$

为了使乘法等于 0，乘法的两个元素之一必须为零。因此，我们将每个因子设置为0：

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

没有解，因为实数没有负根。

现在我们在线上表示所有获得的临界点，即不属于定义域的点（x=-2 和 x=+2）以及取消二阶导数的点（x=0）：

我们评估每个区间内的二阶导数的符号，以了解该函数是凹函数还是凸函数。因此，我们在每个区间中取一个点，看看该点的二阶导数的符号是什么：

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

如果二阶导数为正，则表示该函数是凸函数。

$(\bm{\cup})$

，如果二阶导数为负，则意味着该函数是凹函数

$(\bm{\cap})$

。因此，凹度和凸度区间为：

凸面

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

凹

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

该函数在三个点上改变曲率，因此有理函数原则上将具有三个拐点，即 x=-2、x=0 和 x=2。然而，虽然在 x=-2 和 x=+2 处曲率发生变化，但这些不是拐点，因为它们不属于函数的域。另一方面，在 x=0 处，曲率发生变化，这属于函数，因此x=0 是函数的唯一拐点。

剩下的就是计算拐点的 Y 坐标：

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

简而言之，有理函数的唯一拐点是坐标原点：

转折点：

$\bm{(0,0)}$

练习3

我们知道函数

$f(x)=x^3+ax^2+bx+c$

通过点

$(3,1)$

, 具有相对极值

$x=1$

，以及一个转折点

$x = 2$

。根据此信息，计算参数值

$a, b$

和

$c$

。

查看解决方案

设函数的拐点为

$x= 2$

意思是

$f''(2)=0$

。因此，我们计算函数的二阶导数

$x= 2$

我们将其设置为 0：

$f(x) = x^3+ax^2+bx+c \ \longrightarrow \ f'(x)=3x^2+2ax+b$

$f'(x)=3x^2+2ax+b \ \longrightarrow \ f''(x)= 6x+2a$

$\left. \begin{array}{l} f''(2)=6\cdot 2+2a\\[2ex] f''(2)=0\end{array} \right\} \longrightarrow 6\cdot 2+2a=0$

我们求解得到的方程来找到参数a的值：

$6\cdot 2+2a=0$

$12+2a=0$

$2a=-12$

$a=\cfrac{-12}{2}$

$\bm{a=-6}$

因此，该函数将是：

$f(x)=x^3+ax^2+bx+c \ \xrightarrow{a \ = \ -6}\ f(x)=x^3-6x^2+bx+c$

此外，该函数有一个极值

$x= 1$

，意思就是

$f'(1)=0$

。因此，我们计算函数的一阶导数

$x= 1$

我们将其设置为 0：

$f(x)=x^3-6x^2+bx+c \ \longrightarrow \ f'(x)=3x^2-12x+b$

$\left. \begin{array}{l} f'(1)=3\cdot 1^2-12\cdot 1+b\\[2ex] f'(1)=0\end{array} \right\} \longrightarrow 3\cdot 1^2-12\cdot 1+b=0$

我们求解得到的方程来找到未知数 b 的值：

$3\cdot 1^2-12\cdot 1+b=0$

$3 \cdot 1 -12 + b = 0$

$3 -12 + b = 0$

$b=+12-3$

$\bm{b=9}$

因此，该函数将是：

$f(x)=x^3-6x^2+bx+c \ \xrightarrow{b \ = \ 9} \ f(x)=x^3-6x^2+9x+c$

另一方面，它们告诉我们函数通过点 (3,1)。也就是说，

$f(3)=1$

。因此，我们可以应用这个条件来求出参数c的值：

$\left. \begin{array}{l} f(3)=3^3-6\cdot 3^2+9\cdot3+c \\[2ex] f(3)=1 \end{array} \right\} \longrightarrow 3^3-6\cdot 3^2+9\cdot 3+c = 1$

我们求解得到的方程来找到值

$b:$

$3^3-6\cdot 3^2+9\cdot 3+c = 1$

$27-6\cdot 9+27+c = 1$

$27-54+27+c = 1$

$c=1-27+54-27$

$\bm{c=1}$

因此，该函数将是：

$f(x)=x^3-6x^2+9x+c \ \xrightarrow{c \ = \ 1} \ f(x)=x^3-6x^2+9x+1$