函数与轴的交点或交点

17 9 月, 2023

本页介绍了函数与笛卡尔轴的交点（或交叉点）以及如何计算它们。此外，您还会找到几个示例来充分理解它们是如何找到的，您甚至可以通过逐步解决的练习进行练习。

函数与轴的交点（或交叉点）是什么？

在了解如何计算它们之前，让我们记住函数与轴的交点是什么。

交点或轴交点是函数表示与坐标轴相交的点，即图形上绑定到 X 轴和 l 轴的点。 Y 轴。

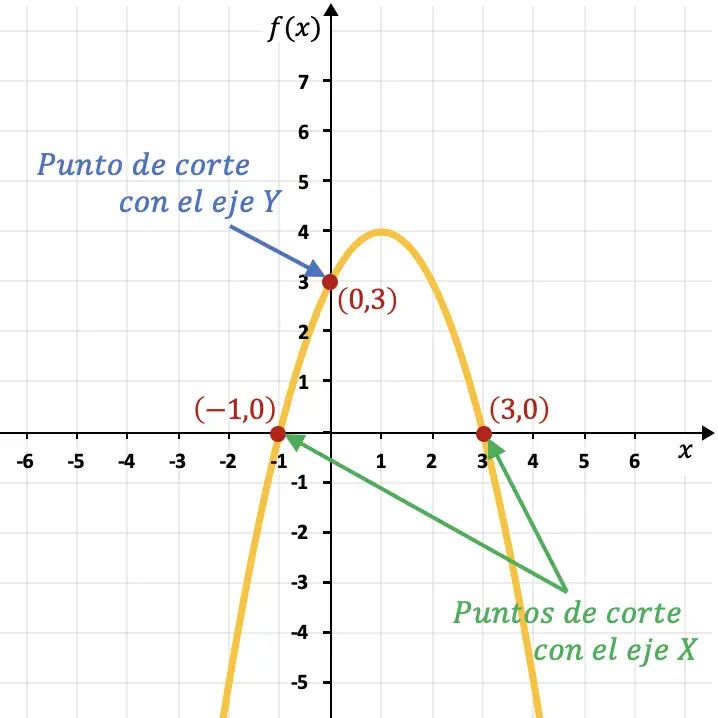
例如，下图中的抛物线与 Y 轴相交于点 (0,3)，与 X 轴相交于点 (-1,0) 和 (3,0)。

函数与轴的交点或交点

函数与 X 轴的割点

函数与 X 轴交点的第二个坐标始终为 0，因此：

任何 x 轴函数 OX 的截止点的形式为

$(a,0)$

，并且可以通过求解以下方程来计算：

$f(x)=0$

有时，在求解该方程时，我们可以得到两个（或多个）解，这意味着该函数与 X 轴相交两次（或多次）。另一方面，如果方程无解，则意味着该函数不与 X 轴相交。

函数与 Y 轴的割点

函数与 Y 轴交点的第一个坐标始终为 0，因此：

任何具有 y 轴 OY 的函数的截止点的形式为

$(0,a)$

，可以通过计算函数在 x=0 处的图像来求得：

$f(0)$

与 X 轴上的断点不同，Y 轴上只能有一个断点。

使用轴计算函数截止点的示例

为了让您没有疑问，我们将在下面看到如何使用笛卡尔轴查找函数的割点的示例：

以数字方式求出以下函数的截止点：

$f(x)=-2x+4$

我们首先计算函数与 x 轴的截止点。与 X 轴的交点的第二个分量始终等于 0，也就是说，它将属于以下类型

$(a,0)$

。因为在 OX 轴上 f(x) 始终等于 0。因此，要找到该点的另一个分量，我们需要求解方程

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

因此与 X 轴的交点为：

$\bm{(2,0)}$

现在我们将找到与 y 轴的交点。与 Y 轴的交点的第一个分量始终等于 0，也就是说，该点的类型为

$(0,a)$

。由于自变量x总是在 Y 轴上抵消。因此，要找到该点的另一个坐标，我们需要计算

$f(0):$

$f(0)=-2 \cdot 0+4=4$

因此与 Y 轴的交点为：

$\bm{(0,4)}$

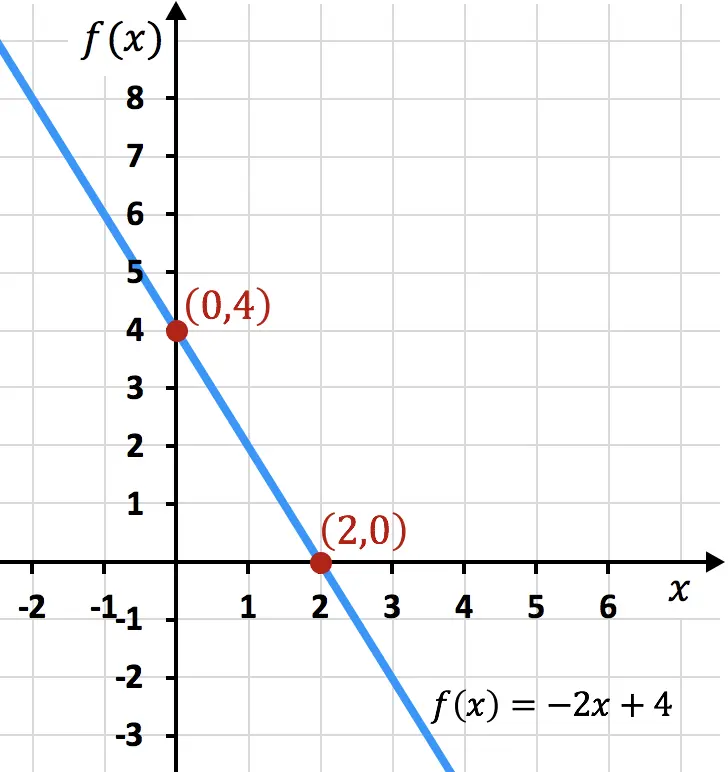
下面以图形方式显示了示例函数，您可以看到找到的阈值与图中的阈值一致：

如何找到带有轴的函数的割点

已解决带轴函数割点的练习

练习1

用下列函数的坐标轴确定切削点：

$f(x)=3x-3$

查看解决方案

X轴切削点

为了找到函数与 X 轴的交点，需要求解

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

因此，函数与 X 轴的交点为：

$\bm{(1,0)}$

Y轴切削点

要找到与 Y 轴的交点，您必须计算

$f(0):$

$f(0)=3\cdot 0 -3= -3$

因此，函数与 Y 轴的交点为：

$\bm{(0,-3)}$

练习2

找到以下仿射函数与笛卡尔轴的交点：

$f(x)=2x+8$

查看解决方案

X轴切削点

为了找到函数与 OX 轴的极限点，我们需要将函数设置为零并求解所得方程：

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

所以函数与横坐标轴的交点为：

$\bm{(-4,0)}$

Y轴切削点

为了找到 OY 轴的截止点，我们需要计算

$f(0):$

$f(0)=2\cdot 0 +8= 8$

因此，函数与计算机轴的交点为：

$\bm{(0,8)}$

练习3

使用以下二次函数的轴计算截止点：

$f(x)=x^2-3x+2$

查看解决方案

X轴切削点

为了找到函数与 X 轴的交点，需要求解

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

在这种情况下，我们需要求解二次方程，因此我们应用以下公式：

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

我们得到了二次方程的两个解，因此函数与 X 轴相交于两点：

$\bm{(1,0)} \qquad \bm{(2,0)}$

Y轴切削点

另一方面，为了确定与Y轴的交点，需要计算

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

因此，函数与 Y 轴的唯一交点是：

$\bm{(0,2)}$

练习4

找到以下有理函数的笛卡尔平面轴的交点：

$f(x)=\cfrac{5}{x}$

查看解决方案

X轴切削点

为了找到函数与 X 轴的交点，需要求解

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5 不等于 0，因此方程无解，因此函数和 X 轴之间没有交点。

Y轴切削点

要找到与 Y 轴的交点，您必须计算

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

任何数字除以零都是不确定的，会得到无穷大。因此，该函数在任何点都不会超出 Y 轴。

简而言之，练习函数与轴没有交点，即它的图形在任何点都不经过X轴或Y轴。

练习5

使用以下三次函数的轴计算截止点：

$f(x)=x^3-9x$

查看解决方案

X轴切削点

为了找到函数与 X 轴的交点，需要求解

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

方程的两项都有一个x ，我们可以用它提取一个公因子：

$x(x^2-9)=0$

为了满足前面的等式，其中一个因子必须为 0。因此，我们将每个因子设置为零，以获得所有可能的解：

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

因此，我们得到了三次方程的三个解，因此该函数将 X 轴切割为 3 个点：

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

Y轴切削点

要计算与Y轴的切割点，您需要计算

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

因此，函数与Y轴的唯一交点是坐标原点(0,0)：

$\bm{(0,0)}$

请注意，我们在计算与 X 轴的切割点时已经找到了该点，因为该函数同时与两个轴在该点进行切割。

发表评论取消回复