在本文中,我们解释如何导出函数(公式)的减法。您还将找到减法导数的示例和已解决的分步练习来练习。
减法的导数公式
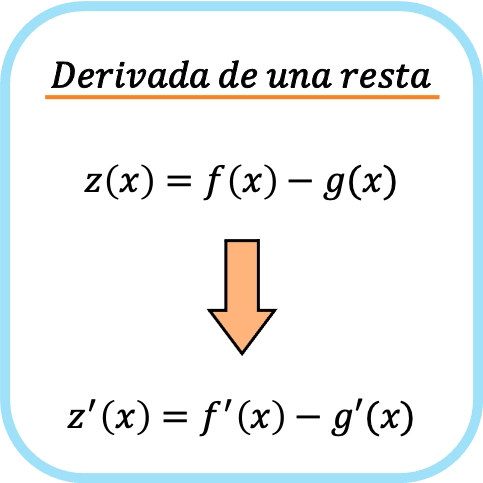
两个函数相减的导数等于分别减去每个函数的导数。
![]()
换句话说,对两个函数分别求导然后相减,相当于先将函数相减,然后求导。
同样,相同的微分规则适用于两个或多个函数的减法,因此如果我们有三个、四个、五个……函数的减法,我们需要分别对每个函数进行微分,然后将它们相减。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc282473a7f7560eebc97db66bb8f54_l3.png)
正如您所看到的,函数差的导数公式与和的导数规则非常相似。
➤请参阅:函数和的导数
减法导数的例子
一旦我们了解了减法导数的公式是什么,我们现在就继续分析此类运算的导数的几个示例,以充分理解函数的减法是如何导出的。
示例 1:势函数减法的导数
![]()
两个函数相减的导数相当于每个函数各自的导数之差。因此,我们首先分别计算每个函数的导数:
![]()
![]()
因此整个函数的导数如下:
![]()
示例 2:不同函数减法的导数
![]()
要对减法函数求导,必须首先对两个函数分别求导,然后再将它们相减。
![]()
![]()
在求出两个导数后,我们以相同的初始顺序将它们相减:
![]()
示例 3:平方减法的导数
![]()
在本例中,我们有一个复合函数,因为它是三个平方函数之间的减法。因此,我们必须使用势函数的导数公式和链式法则来计算整个函数的导数:
![]()
➤请参阅: 幂导数公式
已解决减法导数的练习
导出以下函数的减法:
![]()
![]()
![]()
![]()
![]()
查看解决方案
![]()
![]()
![]()
![]()
![]()
减法导数的证明
接下来,我们从导数的定义来演示函数减法的导数公式,即:
![]()
因此,如果 z 是两个不同函数的差:
![]()
![]()
我们将 z 替换为极限表达式中函数的减法:
![]()
![]()
我们现在将进行转换以分离分数并获得两个分数的减法:
![]()
![]()
通过应用极限定律,我们可以将上述表达式分成两个不同的极限。因为减法的极限等于极限的减法:
![]()
如果仔细观察,每个极限都对应于一个函数的导数,这意味着满足差值导数的公式:
![]()