在本页中,您将了解什么是共面向量以及如何判断 2、3、4 或更多向量是否共面。此外,您将能够看到逐步解决共面向量的示例和练习。
什么是共面向量?
在解析几何中,共面(或共面)向量的含义如下:
共面向量是属于同一平面的向量。
因此,两个向量总是共面的,因为一个平面只需 2 个向量即可形成。另一方面,当存在3个、4个或更多个矢量时,其中一个矢量可能不包含在同一平面中,因此它们不共面。
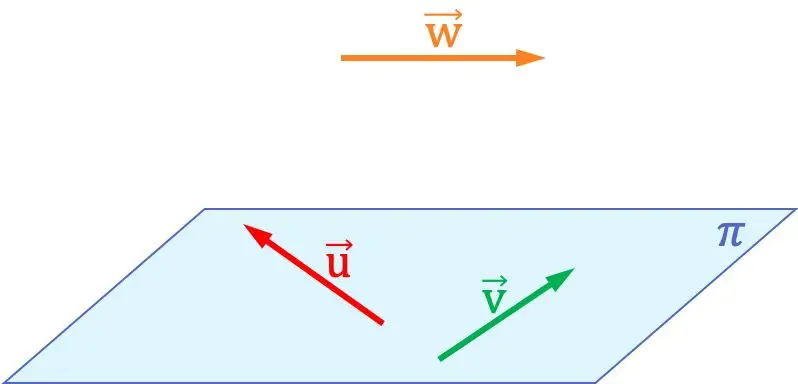
例如,在上图中您可以看到向量
![]()
和
![]()
它们彼此共面,因为它们包含在同一平面中。另一方面,这两个向量与向量不共面
![]()
,因为在包含三个向量的空间中无法形成平面。
从这个属性我们可以推断,如果 3 个或更多向量共面,则定义所述向量的点(向量的起点和终点)也是共面点。
向量什么时候共面?
正如我们在共面(或共面)向量的定义中看到的,两个向量始终共面,但两个以上的向量不必遵守共面关系。
因此,有几种方法可以确定三个或更多向量是否共面:
- 如果三个向量的混合积(或三重点积)等于零,则表示三个向量共面。如果您不太清楚这个运算是如何计算的,我建议您看一下什么是三个向量的混合积,在这里您可以找到解释以及示例和已解决的练习。
![]()
- 如果一组向量可以表示为两个向量的线性组合,则意味着它们是共面的,这意味着 3 个或更多向量当且仅当它们线性相关时才是共面的。为了表明三个或更多向量是两个向量的线性组合,所有向量形成的矩阵的秩等于2就足够了。
![]()
重要的是,您必须充分理解线性相关性和独立性的概念,即两个向量何时线性相关或线性独立以及这意味着什么。如果您不完全清楚,在链接中您会找到非常详细的解释,此外,您还可以看到逐步解决的示例和练习。
- 如果所讨论的向量是平行向量,则意味着它们也是共面的,即所有平行向量都包含在同一平面中。
![]()
解决了共面向量的问题
练习1
判断以下三个向量是否共面:
![]()
![]()
![]()
要检查这是否是 3 个共面向量,我们必须计算这三个向量之间的混合积:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a1e4b0655c0a3f0165c880f5e64cce0_l3.png)
三个向量的混合积为零,因此三个向量共面。
练习2
判断以下三个向量是否共面:
![]()
![]()
![]()
检查我们是否正在处理 3 个共面向量的一种方法是求解三个向量之间的混合积。然而,如果我们仔细观察向量的分量,我们可以看到它们是成比例的。因此,这三个向量彼此平行。
![]()
由于所有向量都是平行的,因此它们实际上是 3 个共面向量。
练习3
判断下列四个向量是否共面:
![]()
![]()
![]()
![]()
要知道四个向量是否共面,我们必须计算所有向量组成的矩阵的秩:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8384924c86edafd568505d5f80e1705d_l3.png)
在这种情况下,我们通过行列式计算所述矩阵的范围:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2778435c7f53952adf072419af8b268c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-82f278494a221879cc86da92ab4378c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-889142ac348173dd6c838633007f2d06_l3.png)
![]()
所有向量组成的矩阵的秩等于2,因此4个向量共面。
练习4
计算参数值
![]()
使得以下 4 点共面:
![]()
![]()
![]()
![]()
为了使四个点共面,由它们确定的向量必须共面。因此我们计算这些向量:
![]()
![]()
![]()
其向量矩阵为:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
为了使所得向量共面,矩阵的秩必须为 2。因此,整个 3×3 矩阵的行列式必须为 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
最后我们解决了未知的问题
![]()
![]()
![]()