在这里,您将找到关于余数定理(或余数定理)是什么以及如何将其应用于多项式的解释。您还可以查看示例,并通过逐步解决余数定理的练习进行练习。
什么是余数定理?
在数学中,余数定理表示任何多项式 P(x) 除以另一个 (xa) 形式的多项式的余数等于多项式 P(x) 的数值,其中值 x=a,换句话说,除法 P(x):(xa) 的余数等于 P(a)。

余数定理的例子
了解了余数定理是什么后,让我们看一下其应用的实际示例:
- 计算以下两个多项式除法的余数:
![]()
![]()
为了找到多项式除法的余数(或残差),我们可以利用余数定理,因为在这种情况下,除法多项式的形式为 (xa),也就是说它是一次,系数变量 x 为 1 并且有一个独立项。
因此,我们应用余数定理,该定理表明,像这样的除法的余数等于在变号除数多项式的独立项中计算的被除数多项式的数值,即 P (1)。

因此,为了找到除法的余数,我们需要计算 x=1 处的多项式:
![Rendered by QuickLaTeX.com \begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff03f53066d698ee3d76e0024f3b51ac_l3.png)
因此,多项式除法的余数为 2 。
另一方面,我们还可以用鲁菲尼多项式除法规则来检查余数是否与我们发现的结果一致:
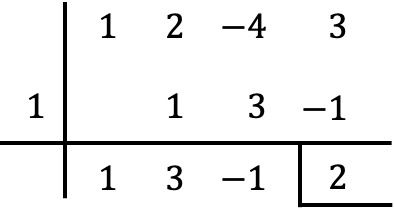
正如您所看到的,使用余数定理确定多项式除以二项式的余数比使用鲁菲尼规则更快、更容易,因为执行的计算要少得多。
余数和因数定理
从余数定理和多项式的根(或零)的定义,我们可以推导出因子定理。因此,因子定理意味着:
因子定理表明,当且仅当 P(a)=0 时,多项式 P(x) 才能被 (xa) 形式的另一个多项式整除。并且,在这种情况下,这意味着 a 是多项式 P(x) 的根或零。
此外,根据余数定理,这意味着如果一个多项式可被另一个多项式整除,则所述除法的余数为零,因为P(a)=0。
例如,如果我们有某个多项式:
![]()
该多项式可被二项式 (x-2) 整除,因为 P(2)=0:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e90c14ff06cdfa041299e016051b1dd_l3.png)
由于x=2抵消了多项式P(x),这意味着x=2是所述多项式的根。
进一步,由于 P(2)=0,根据余数定理我们可以知道除法的余数
![]()
等于 0。
余数定理的解答练习
为了完成余数定理的理解,我们准备了一些逐步解决的练习,以便您练习。我们建议您先亲自尝试一下这个练习,然后检查您是否做对了。
练习1
通过余数定理求多项式除法的余数
![]()
,是参与运算的多项式:
![]()
除数多项式仅由一次项和独立项组成,而且一次项的系数为1。因此,我们可以利用余式定理。
为了应用余数定理,用除数多项式改变符号的独立项来计算被除多项式就足够了,或者换句话说,我们必须计算P(2)。
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23790b78a8463a23a7b8202ab544ade9_l3.png)
因此,两个多项式相除的余数为 21 。
练习2
给定多项式
![]()
求除以下列各项多项式所得的余数:
由于所有除法多项式都满足余数定理的条件,因此我们可以使用该定理来确定每次除法的余数:
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8ae7d7c667bf9ca6bd7417356756447_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2a31e7c1334f8d1a24ba246d0459e4e_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e8191f6ce490a0786515d84efaf45ec_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d2e1e17bbcf91abb36d8cad24cadf0c_l3.png)
练习3
计算参数应该值多少
![]()
这样多项式除法的余数
![]()
等于 3,均为多项式:
![]()
在这种特殊情况下,除法多项式由一次单项式和一个独立项组成,而且一次单项式的系数为1。因此,我们可以使用余数定理。
要使用余数定理,只需用符号变化替换除法多项式的独立项,其中除法多项式中有 x,因此我们必须求解 P(-3)。
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-693cd65a618f884d0dd1be2f20594229_l3.png)
但显然我们得到的结果是基于未知数
![]()
然而,问题陈述告诉我们余数必须等于 3,因此我们必须将找到的余数设置为等于 3:
![]()
最后,我们求解方程:
![]()
![]()
![]()
![]()
练习4
用因子和余数定理确定多项式是否
![]()
可被多项式整除
![]()
![]()
使得多项式
![]()
可被多项式整除
![]()
这两个多项式之间的除法必须精确,因此余数必须为零。
那么,由于除数多项式是
![]()
由因子定理和余数定理,我们知道多项式
![]()
将被多项式整除
![]()
如果已满
![]()
因此,我们必须看看这个等式是否得到验证:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e8793835809000092b15eaec3877c18_l3.png)
事实上,该部门的其余部分
![]()
等于 0,所以多项式
![]()
是的,它可以被另一个多项式整除
![]()
你觉得这个解释怎么样?你喜欢它吗?希望如此!不要忘记您可以在评论中给我们留下您的建议或问题。 ⬇⬇⬇ 我们读了你们全部! 😁😁