在本文中,我们解释什么是函数的周期性。此外,您还将看到几个周期函数的示例。最后,我们将分析三角函数的周期,因为它是三角函数最重要的特征之一。
什么是函数的周期性?
函数的周期性是函数周期性地重复其值的特征,也就是说,如果一个函数的图形每隔一定的时间间隔重复一次,那么该函数就是周期性的。这个间隔称为周期。
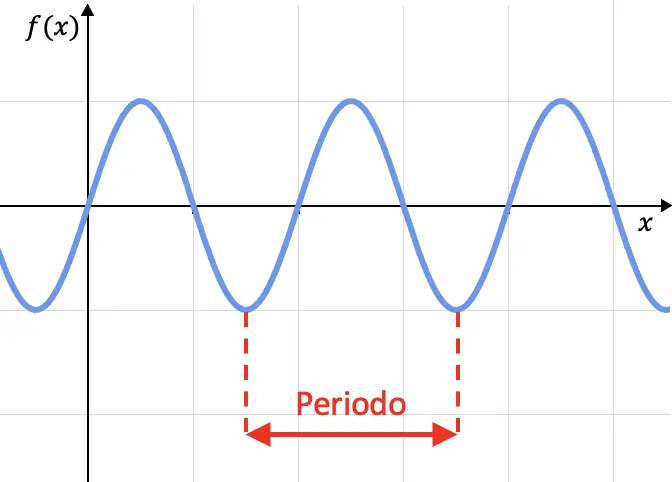
数学上,如果函数仅满足,则定义为周期性函数
![]()
对于自变量 x 的任意值。
![]()
其中T是周期函数 i k的整数周期。
函数周期性的示例
一旦我们了解了函数周期性的概念,我们就会看到几个如何计算函数周期性的示例。
实施例1
判断下列函数是否是周期函数:
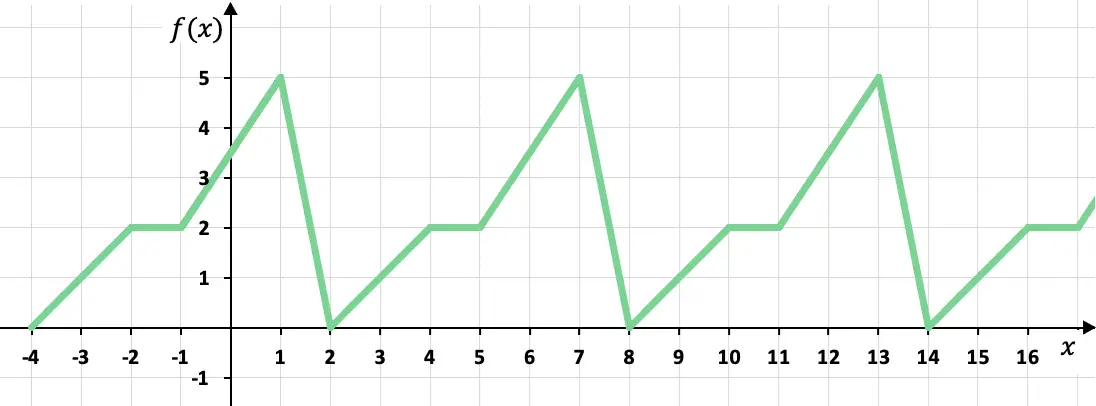
这个分段定义的函数是周期函数,因为其图的值循环重复。更准确地说,该函数每 6 个 x 取相同的值,因此该函数的周期等于 6。
![]()
实施例2
求以下函数的周期性:
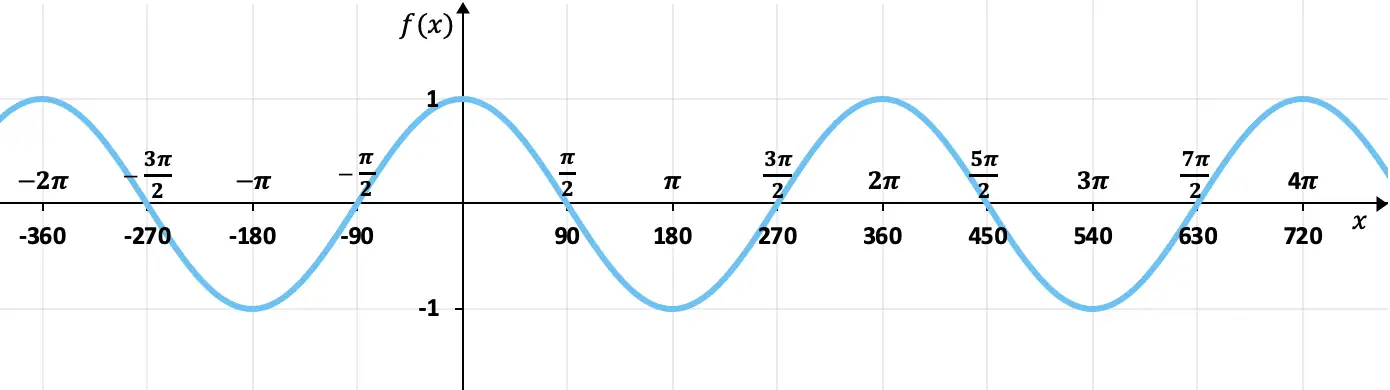
该函数对应于三角函数的图形表示,更准确地说是余弦函数。
从图中我们可以看出,该函数周期性地重复其值,因此它是一个周期函数。此外,波峰与波峰之间有 2π(或 360°)的间隔,因此这就是函数的周期。
![]()
三角函数的周期性
周期性与三角函数密切相关,事实上,此类函数的主要特征之一是大多数三角函数都是周期性的。
接下来,我们将研究 3 个主要三角函数的周期性:正弦、余弦和正切。
正弦函数周期
正弦函数的表达式如下:
![]()
在这种情况下,不需要绘制函数图像来查找其周期,而是可以简单地通过应用以下公式来计算:
![]()
此外,正弦函数还有一个特殊性:如果我们改变它的周期,我们也会改变它的图形的形状。您可以在以下链接中查看周期值如何影响其图形表示:
➤请参阅:正弦函数图
余弦函数的周期
余弦函数的代数表达式如下:
![]()
与正弦一样,余弦函数的周期可以直接使用以下公式求得:
![]()
余弦周期的值完全决定了它的图形,请点击以下链接并找出原因:
➤请参阅:余弦函数图
正切函数的周期
正切函数用数学方式描述:
![]()
正切函数周期的计算公式与正弦和余弦相同:
![]()
然而,正切函数图与正弦和余弦不同,因为它也有周期性重复的渐近线。您可以通过以下链接查看此三角函数的此功能和其他功能:
➤请参阅:正切函数的图形