什么是向量的分量以及如何计算向量的分量

在此页面上，您将找到向量的分量（或坐标）的解释。此外，您还可以看到它们是如何从两点计算出来的，甚至是如何通过模块和角度进行分解的。此外，您还会发现逐步解决的示例和练习。

向量由哪些部分组成？

矢量的分量是矢量在笛卡尔轴上的投影。因此，向量在 x 轴上的投影是向量的 X 分量，类似地，向量在 y 轴上的投影是向量的 Y 分量。

向量的分量也可以称为向量的坐标。

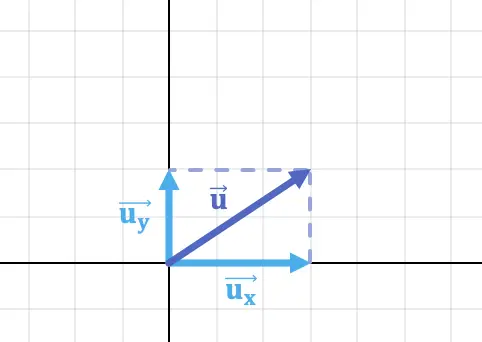
例如，上图中向量的水平分量和垂直分量为：

所以向量是：

因此，向量的分量也可以定义为向量在坐标系中的表示。显然，如果它是二维系统（在 r2 中），则向量将具有两个分量，另一方面，如果它是三维基（在 r3 中），则向量将由三个分量组成。

向量的笛卡尔分量非常重要，因为通过它们我们可以知道向量的特征，主要是向量的方向、方向和模（或幅度）。此外，它们还用于执行向量运算。

如何从两点计算向量的分量

我们刚刚了解了如何以图形方式查找矢量图的坐标，但是，我们也可以通过数字方式确定其分量。

为了对向量的分量进行数值计算，我们需要知道两点：它的原点和终点，或者换句话说，它的起点和终点。由于向量的分量是我们通过减去其末端减去其原点获得的坐标。

例如，我们将计算原点为 A(3,1)、终点为 B(5,4) 的向量：

正如您所看到的，确定向量的分量并不是很困难，但是非常重要。例如，最常用的矢量类型之一是垂直（或正交）矢量；好吧，如果您了解向量的坐标是什么，那么计算垂直向量就非常容易。您可以在正交向量的解释中了解它是如何完成的。

如何根据向量的模数和角度计算向量的分量

您还可以根据向量的大小以及它与 X 轴形成的角度找到向量的分量。这个过程称为向量分解。

因此，矢量的 X 和 Y 分量可以通过余弦和正弦的三角比来计算：

如图所示，向量的模及其分量构成一个直角三角形，因此可以应用三角学的初等公式。

如果你不记得向量的模是如何计算的，你可以查一下向量的模是多少。在这里，您将找到向量大小的公式、示例、逐步解决的练习以及向量大小的所有属性。这是一个非常完整的解释，所以你会完全理解它。 ✅

与始终为正的向量的大小不同，它的分量可以为负，因为正弦和余弦可以取负值。

例如，我们将对模数和与 OX 轴的角度为的向量进行向量分解：

向量的 X 分量等于模乘以角度的余弦：

向量的 Y 分量等于模与角度正弦的乘积：

所以向量的坐标为：