在此页面上,您将找到二项式是什么的解释,此外,您还可以看到每种类型二项式的示例。此外,我们还向您展示用于解决二项式运算的公式:二项式乘法、二项式平方、二项式立方……
什么是一对?
在代数中,二项式的定义是:
二项式是仅由两个单项式组成的多项式。换句话说,二项式由一个代数表达式组成,该代数表达式仅包含由加号 (+) 或减号 (-) 连接的 2 个不同项。

二项式一词来自希腊语,由两个词汇成分( bi和nomos )组成,含义如下:
- bi : 前缀,意思是 2。
- nomos :意思是部分。
因此,我们可以推导出二项式的含义:具有两部分(或2个单项式)的多项式。
另一方面,“配对”的概念还有数学意义之外的另一种含义,即“配对”还可以指在政治生活、某些体育学科甚至娱乐领域中起主导作用的一组两个人物。 。但是,显然,我们在这里将重点关注二项式的数学定义。
二项式的例子
为了完成对二项式概念的理解,我们将看到此类多项式的几个示例:
- 二次二项式的示例:
![]()
- 三阶二项式的示例:
![]()
- 四次二项式的示例:
![]()
现在我们知道什么是二项式,我们将了解二项式的不同类型以及如何解决二项式运算。
二项式平方
平方二项式是显着恒等式,也称为显着乘积或显着等式。求解二项式 2 的幂取决于它是和二项式还是差二项式。
二项式和是指两项均为正的二项式,也就是说二项式平方和为:
![]()
另一方面,差(或减)二项式是加法二项式的共轭,也就是说,它的一个单项式具有负号。因此,二项式差平方的代数表达式为:
![]()
要计算平方二项式,您必须应用一个公式,正如我们所见,该公式根据是加法还是减法而变化。了解这是如何在显着等式的公式中完成的,您可以在其中看到所有分步解释以及示例和已解决的练习,并且不仅是这两个显着等式,而是所有这些等式。
二项式立方
尽管不太常用,立方二项式也被认为是著名的产品。或者换句话说,有一些数学规则可以让您快速找到二项式的立方(您可以在上面著名的恒等式公式的链接中看到它们)。
和之前一样,这个增强的结果取决于它是否是总和的立方:
![]()
或者相反,如果幂由差值或减法的立方构成:
![]()
从逻辑上讲,平方二项式和立方二项式之间的主要区别在于幂指数。然而,三次二项式的公式比平方二项式的公式复杂得多。
值得注意的协议
特别是某些类型的二项式由于其特征而有些特殊,因为它们对应于鲜为人知的显着身份(或显着产品)。
- 平方和:
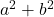
- 平方差(或减法):
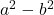
- 立方和:
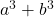
- 立方的差(或减):
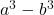
金子
![]()
和
![]()
是任意两个单项式。
虽然这些二项式表达式看起来很像我们上面看到的那些(二项式平方和二项式立方),但如果仔细观察它们是不同的。从这个意义上说,您还可以通过单击上面的链接 ⬆ 显着恒等式的公式来查看显着二项式的公式及其推导。⬆
二项式乘法
二项式最常见的运算之一是乘法。接下来我们将看到一个如何计算二项式之间的乘法的示例。
![]()
要计算二项式乘法,我们必须首先将第一个二项式中的每一项乘以第二项式中的每一项:
![]()
![]()
接下来,我们将相似的术语分组,即它们具有相同的字面部分:
![]()
通过这种方式,我们设法找到了两对之间的乘积的结果。
具有共同项的两个二项式的乘积
当参与乘法的二项式以变量作为公项时
![]()
有一个公式可以快速计算这个二项式运算:
![]()
在这里,我们向您展示一个已解决的练习,以便您了解如何应用此公式:
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
牛顿二项式
牛顿二项式,也称为二项式定理,是用于计算二项式幂的公式。
牛顿二项式的数学公式如下:
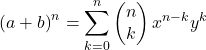
或同等学历:
![]()
正如您所看到的,这个公式理解起来有点复杂。这就是为什么我们将最低次二项式的幂制作如下,以便您更好地理解:

这个公式对于计算二项式的平方或立方可能有点乏味,因为正如我们上面看到的,有更简单的公式。然而,牛顿二项式对于求更高次方的幂非常有用,例如,它被广泛用于确定四次二项式。
但要应用这个公式,你必须知道如何计算组合数,即类型的代数表达式
![]()
,计算并不容易。 🔍这就是为什么我们建议您在右上角的搜索引擎中搜索这是如何完成的🔎,您会找到我们的文章,我们将逐步向您解释此操作。