本页解释了什么是二次函数及其所有特征:曲率、顶点、与轴的交点等。您还将学习如何在图形上表示二次函数。最后,您可以通过示例、分步练习和二次函数问题进行练习。
什么是二次函数?
二次函数的定义如下:
在数学中,二次(或抛物线)函数是 2 次多项式函数,即最高次项为二次的函数。因此,二次函数的公式为:
![]()
金子:
-
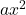
是二次项。
-
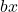
是线性项。
-

是独立项。
二次函数的域始终由实数组成。
![]()
二次函数的凹性和凸性
分析二次函数或抛物线函数的曲率非常简单,因为它仅取决于二次系数。
- 如果系数

为正,二次函数是凸函数(形式为

)。因此,登顶是最低限度。
- 如果系数

为负,二次函数是凹的(形状像

)。因此峰值是最大值。


注意:数学界仍然没有完全同意,因此,一些教授提出了相反的说法:他们将形状为 a 的函数称为凹函数
![]()
,以及一个凸函数,其形式为
![]()
。无论如何,重要的是什么形式具有功能,无论名称如何。
二次函数的顶点
要绘制二次函数的图形,必须知道抛物线顶点的坐标。
为了找到二次函数的顶点,我们需要使用以下公式计算该点的 X 坐标:
![]()
然后我们可以通过计算该点函数的图像来找到另一个顶点坐标:
![]()
因此,二次函数(或抛物线)的顶点坐标为:
![]()
用二次函数的轴切割点
抛物线总是与 y 轴(Y 轴)相交,这种情况发生在
![]()
因此,要计算二次函数与 Y 轴的截止点,必须求解
![]()
例如,以下二次函数与 OY 轴的交点为:
![]()
![]()
![]()
另一方面,二次函数与 x 轴(X 轴)的截止点出现在
![]()
因此,要计算与 X 轴的交点,您必须求解方程
![]()
作为例子,下面是同一个二次函数的 OX 轴截止点的计算:
![]()
![]()
我们用一般公式求解二次方程:
![]()
![]()
因此,二次函数与 X 轴的交点为:
![]()
在这种情况下,我们只能得到二次方程的一个解,但我们可以得到两个解。在这种情况下,这意味着二次函数在两个不同的点处与 X 轴相交。
二次函数或抛物线函数的表示示例
让我们通过示例了解如何在图形上表示二次函数。
- 绘制以下函数的图形:
![]()
首先要做的是计算抛物线的顶点。为此,我们使用上面看到的公式:
![]()
一旦我们知道顶点在哪里,我们就需要构建一个值表: 我们计算顶点及其周围点的函数值:
![]()
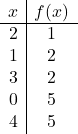
您还可以计算二次函数与笛卡尔轴的割点,以更好地绘制抛物线,但这并不是绝对必要的。
我们现在在图表上表示获得的点:
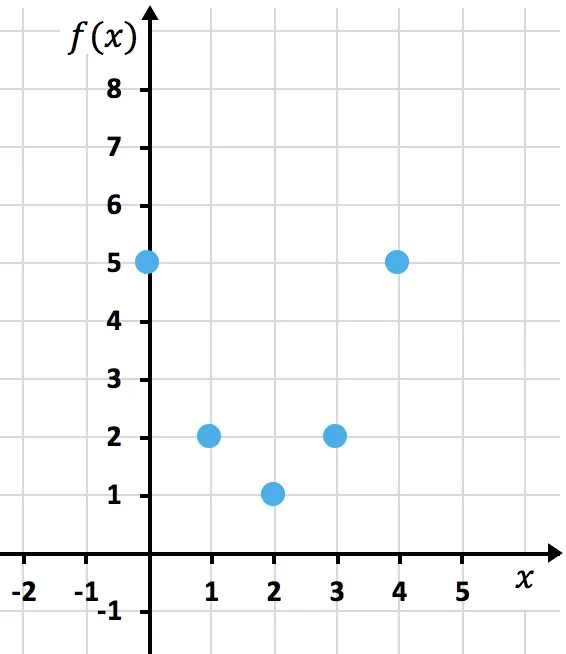
最后,我们将形成抛物线的点连接起来。然后我们拉长抛物线的分支以表明它继续向上:

解决了二次函数的练习
练习1
找到以下二次函数的顶点:
![]()
我们首先使用以下公式计算顶点的 X 坐标:
![]()
现在我们通过计算该点的函数来计算另一个坐标:
![Rendered by QuickLaTeX.com \begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6067325564a5af06f7384d76157f3aa_l3.png)
因此,二次函数的顶点为:
![]()
练习2
找到以下函数与轴的分界点:
![]()
为了计算Y轴的切点,我们需要计算
![]()
![]()
因此,该函数在以下点穿过 Y 轴:
![]()
为了找到 X 轴的切点,我们需要解决
![]()
![]()
![]()
我们用以下公式计算二次方程的根:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d909ba6581faf5916f0b1c0df7e471f_l3.png)
因此,该函数在两个点处切割 X 轴:
![]()
练习3
绘制以下二次函数的图形:
![]()
这是一个二次函数。因此,要表示它,您必须首先使用以下公式计算抛物线顶点的横坐标:
![]()
现在我们创建值表。为此,我们计算
![]()
在顶部和顶部周围:
![]()
![]()
![]()
![]()
![]()
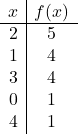
最后,我们在图表上绘制点并绘制抛物线:

练习4
绘制以下二次函数的图形:
![]()
这是二阶函数。因此,要表示它,您必须首先使用以下公式找到抛物线顶点的横坐标:
![]()
现在我们构建值表。为此,我们计算
![]()
在顶部和顶部周围:
![]()
![]()
![]()
![]()
![]()

最后,我们在图上绘制点并绘制抛物线:

练习5
在图上绘制以下不完全二次函数:
![]()
它是二次多项式函数。因此,要表示它,您必须首先使用以下公式计算抛物线顶点的横坐标:
![]()
在这种情况下,该函数是不完整的,因为它没有一次项。为了那个原因
![]()
现在我们制作值表。为此,我们计算
![]()
在顶部和顶部周围:
![]()
![]()
![]()
![]()
![]()

最后,我们在图上绘制点并绘制抛物线:

练习6
解决以下与二次函数相关的问题:
生产产品的成本由以下函数定义:
![]()
金子
![]()
是生产的单位(以千为单位)和
![]()
是单位的生产成本(以千欧元为单位)。
- 用图表表示生产成本函数。
- 确定应生产多少万件才能最大限度地降低成本。
这是一个二次函数。因此,要表示它,您必须首先使用以下公式找到抛物线顶点的横坐标:
![]()
现在我们制作值表。为此,我们计算
![]()
在顶部和顶部周围:
![]()
![]()
![]()
![]()
![]()
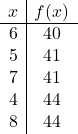
现在我们在图上绘制点并绘制抛物线:
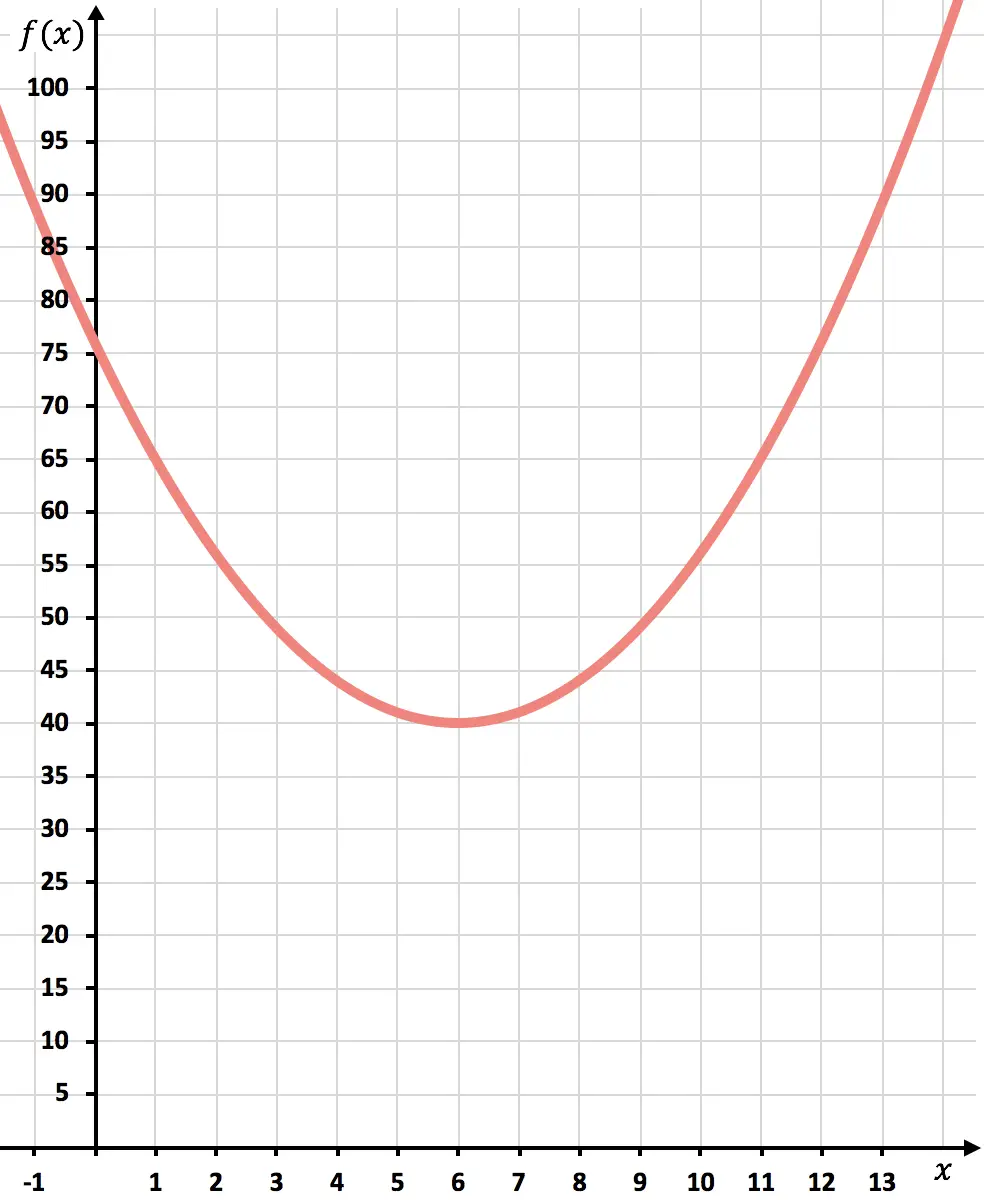
一旦函数被表示出来,我们就会看到成本被最小化了多少。
如图所示,在抛物线的顶部将达到最低成本。因为那是函数取最小值的地方。
总之,生产 6,000 件可将成本降至最低。
练习7
解决以下二次函数问题:
运动员进行标枪投掷,其轨迹可以用以下函数表示:
![]()
金子
![]()
标枪覆盖的米数是
![]()
它的高度(也以米为单位)。
标枪的最大高度是多少?
这是一个二次函数,因此标枪的轨迹将是一条抛物线。
另外,由于二次项的系数为负(-0.025),因此抛物线将呈倒U形,并且其分支将向下。因此,标枪将在顶部达到最大高度,因为这将是抛物线的最高点。
因此,我们用以下公式计算抛物线顶点的横坐标:
![]()
然后我们通过评估函数来计算此时标枪的高度
![]()
![]()
因此,标枪可以达到的最大高度为 42 米。
练习8
解决以下有关二次函数的问题:
公司的生产成本(以欧元为单位)由以下函数定义:
![]()
金子
![]()
是生产的单位。
每套售价为 520 欧元。
- 如果销售 150 台,公司将获得多少利润?
- 应该出售多少单位才能获得最大利润?
该公司每售出一件产品即可赚取 520 欧元。因此,定义收入的函数为:
![]()
金子
![]()
是已售出的单位。
但他们问我们利润,即收入减去成本。因此,我们减去收入减去成本以获得描述公司利润的函数:
![]()
![]()
![]()
![]()
一旦我们知道了描述公司利润的函数,只需将 150 代入函数表达式即可计算公司出售 150 单位将获得的利润:
![Rendered by QuickLaTeX.com \begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f5e6f3101145bcf1a2ece4db3e07c4e_l3.png)
因此,通过销售 150 台,公司将获得 12,500 欧元的利润。
该声明还要求我们计算获得最大利润的单位数。
描述利润的函数是二次函数,因此它将具有抛物线的形状。由于二次项的系数为负(-1),因此抛物线将呈倒 U 形,并且其分支将向下。因此,最大收益将在顶部获得,因为这是抛物线的最高点。
因此,我们用以下公式计算抛物线顶点的横坐标:
![]()
因此,公司将通过销售 250 台获得最大利润。
另一方面,即使新闻稿没有要求,我们也可以确定出售这 250 单位将获得的利润:
![]()
欧元