在本文中,我们将解释如何导出两个函数(公式)的乘积。此外,您将能够看到函数乘积导数的几个示例,甚至可以练习乘法导数的已解决练习。
乘积的导数公式
两个不同函数的乘积的导数等于第一个函数的导数与第二个未微分函数的导数的乘积加上第一个未微分函数与第二个函数的导数的乘积。
换句话说,如果f(x)和g(x)是两个不同的函数,则两个函数相乘的导数公式如下:
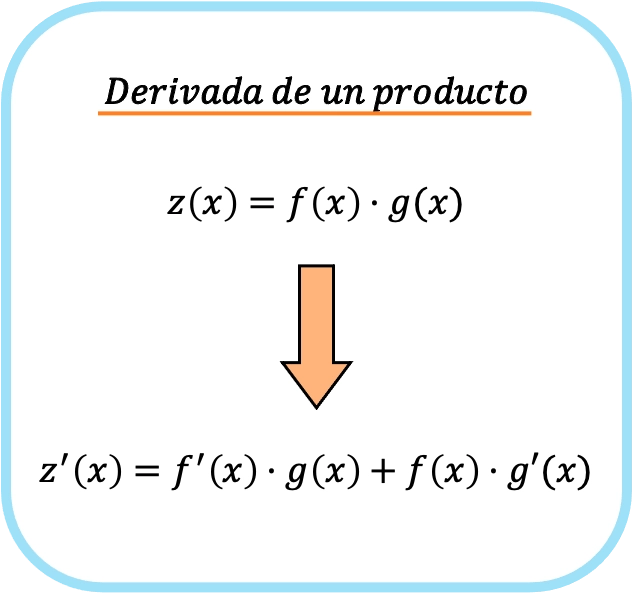
因此,通过应用乘积导数的规则,我们从简单的乘法变为两个不同的乘积。
产品衍生品的示例
一旦我们知道乘积(或乘法)的导数公式是什么,我们将解决此类导数的几个例子。这将使您更容易理解如何导出两个函数的乘积。
实施例1
在此示例中,我们将通过乘法求解两个势函数的导数:
![]()
正如我们在上一节中看到的,乘法导数的公式为:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
因此,我们首先要分别计算每个函数的导数:
![]()
![]()
一旦我们知道了每个函数的导数,我们就可以应用两个函数乘积的导数公式。也就是说,我们将第一个因子的导数与第二个因子不求微分相乘,然后将第一个因子的乘积不求微分地与第二个因子的导数相加:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00f424cf1f72c1d3822c14d49873253e_l3.png)
最后,我们对得到的结果进行简化操作:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-48b8d455b68b87932ca3a437f5ffe3a3_l3.png)
实施例2
在这种情况下,我们将通过函数导出常数的乘积:
![]()
乘积的导数规则如下:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
因此,我们分别导出产品中的每个函数:
![]()
![]()
然后我们应用乘法导数的规则:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c2d81edaa002aeb66ca6eec22bec001_l3.png)
请注意,常数的导数始终为零,因此我们可以推断,常数乘以函数的导数等于常数与函数的导数的乘积。
![]()
实施例3
让我们求解指数函数和自然对数之间的乘积:
![]()
两个函数相乘的导数公式为:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-775fe6e5ac196e5a44c840866e35062d_l3.png)
因此,我们必须首先分别对形成乘积的每个函数求导,如下所示:
![]()
![]()
因此,函数的导出积为:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e1cb417a69252fe05883f7963bcb8db_l3.png)
解决了产品导数的练习
导出以下函数产品:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f46e303cda3be6c3781f7ee4c46c1680_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5dbaa6f333ff27c717b6478d26154025_l3.png)
源自三功能产品
接下来,我们为您提供 3 个函数相乘的导数公式,因为它与 2 个函数的导数公式非常相似,并且在某些情况下很有用。
三个函数乘积的导数等于第一个函数和其他两个函数的导数的乘积,加上第二个函数和其他两个函数的导数的乘积,再加上第一个函数的导数的乘积第三个函数。函数由另外两个函数组成。
![]()
例如,如果我们想导出以下三个不同函数的乘法:
![]()
为了求解导数,我们必须应用三个函数的乘积的导数规则,因此:
![]()
乘积导数公式的演示
最后,我们将演示乘法导数的公式。您不必记住它,但了解公式的来源总是有好处的。 🙂
根据导数的数学定义:
![]()
令函数z为两个不同函数的乘积:
![]()
那么根据定义z的导数将是:
![]()
![]()
我们知道,如果我们通过加减法来添加一项,只要两者是同一项,就不会影响结果。因此,我们可以继续下一步:
![]()
我们现在使用边界属性将先前的边界分成两个不同的边界:
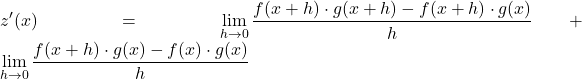
我们提取两个分数分子中的公因数:
![]()
另一方面,我们知道以下极限的结果:
![]()
因此我们可以简化限制:
![]()
![]()
最后,看看剩下的两个极限,每个极限都对应于函数导数的定义。因此,平等可以简化为:
![]()
或同等学历:
![]()