▷ 计算两个向量的叉积（示例）

本页解释了什么是两个向量的叉积以及如何计算它。您还将了解如何使用右手定则（或螺旋形）找到叉积的方向和方向。更重要的是，您会发现此类操作的用途，以及逐步解决的示例、练习和问题。

两个向量的叉积是多少？

在数学中，叉积是三维空间（在 R3 中）中两个向量之间的运算。该向量运算的结果是一个向量，其方向垂直于两个相乘向量，并且其模等于乘数向量的模与它们形成的角度的正弦的乘积。换句话说，它的公式是：

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

正如您在前面的公式中看到的，叉积表示为

$\bm{\times}$

，这就是为什么它也被称为叉积。它有时也被称为吉布斯矢量积，因为他发明了它。

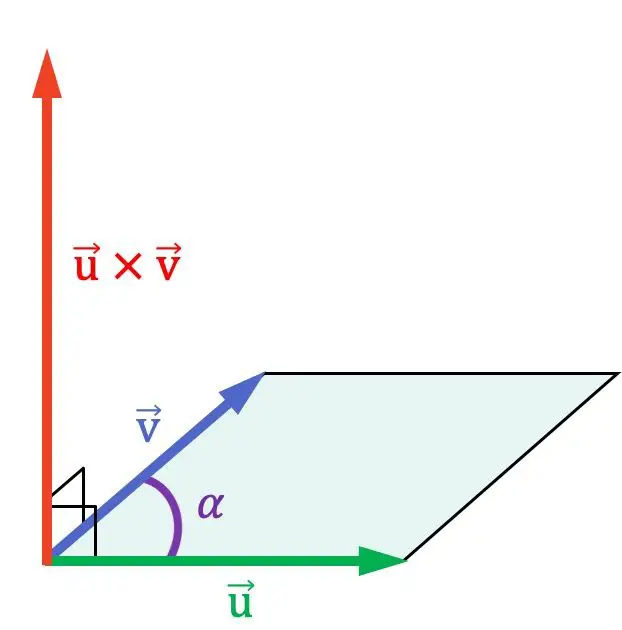
正如您在前面的图形表示中所看到的，叉积垂直于它们相乘的两个向量，因此，它垂直于包含它们的平面。

计算两个向量叉积的公式

如果我们知道向量的笛卡尔坐标，计算它们的叉积的最简单方法是求解 3×3 行列式。观察它是如何完成的：

考虑任意两个向量：

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

其向量积为：

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

其中向量

$\vv{i}, \vv{j},\vv{k}$

这些分别是 X、Y 和 Z 轴方向的单位向量。

让我们看一个如何计算两个向量之间的叉积的示例：

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

为了确定向量之间的向量积，我们必须做出以下 3 阶行列式：

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

在这种情况下，我们将通过佐剂或辅因子来求解行列式（也可以使用 Sarrus 规则）：

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

因此，两个向量的向量积的结果是：

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

确定叉积的方向和方向

有时我们不需要知道叉积得到的向量的分量，但只要找到它的模、它的方向和它的方向就足够了。这在物理学中经常发生，尤其是在力的计算中。

因此，求向量乘积的方向和方向有多种规则，最著名的是右手定则（用三个手指或用整只手）和螺旋定则（或螺丝） 。您可以使用其中任何一个，因此您无需了解所有规则，我们仍会向您解释这三个规则，以便您可以坚持使用您最喜欢的一个。 😉

右手定则（3指）

右手规则或定律的三指版本涉及执行以下步骤：

将右手的食指放在叉积的第一个向量上
$(\vv{\text{u}}).$
将右手的中指（或中指）朝向叉积的第二个向量
$(\vv{\text{v}}).$
生成的拇指位置表示叉积的方向和方向
$(\vv{\text{u}}\times\vv{\text{v}}).$

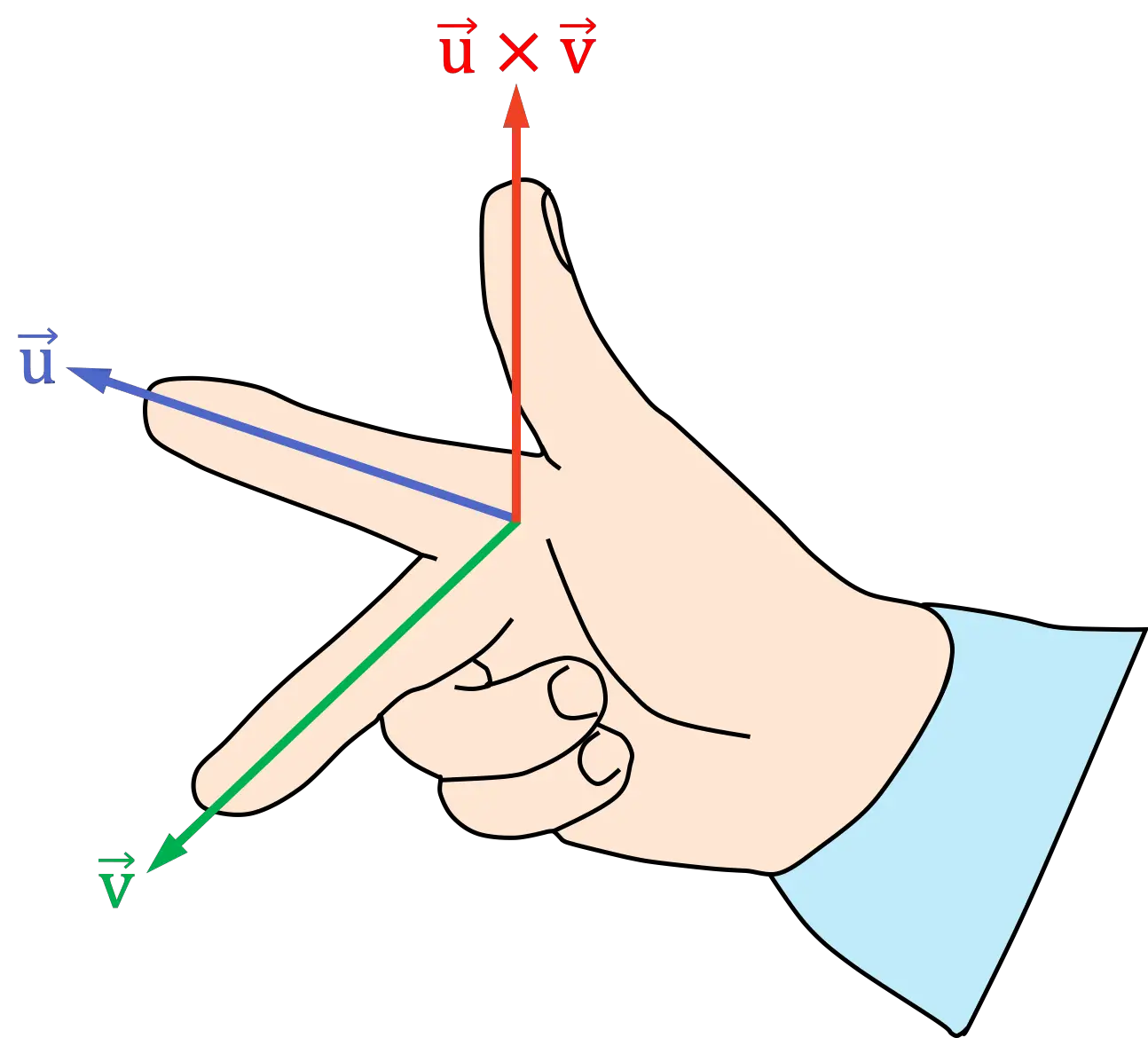
右手定则（手掌）

手掌版本的右手规则或法则与之前的规则非常相似。要应用它，您必须执行以下步骤：

将右手的手指指向与叉积的第一个向量相同的方向
$(\vv{\text{u}}).$
将手指移向叉积的第二个向量，合上右手
$(\vv{\text{v}}).$

您需要将手放在矢量之间的角度（或距离）较小的一侧。
拇指的最终位置决定了叉积的方向
$(\vv{\text{u}}\times\vv{\text{v}}).$

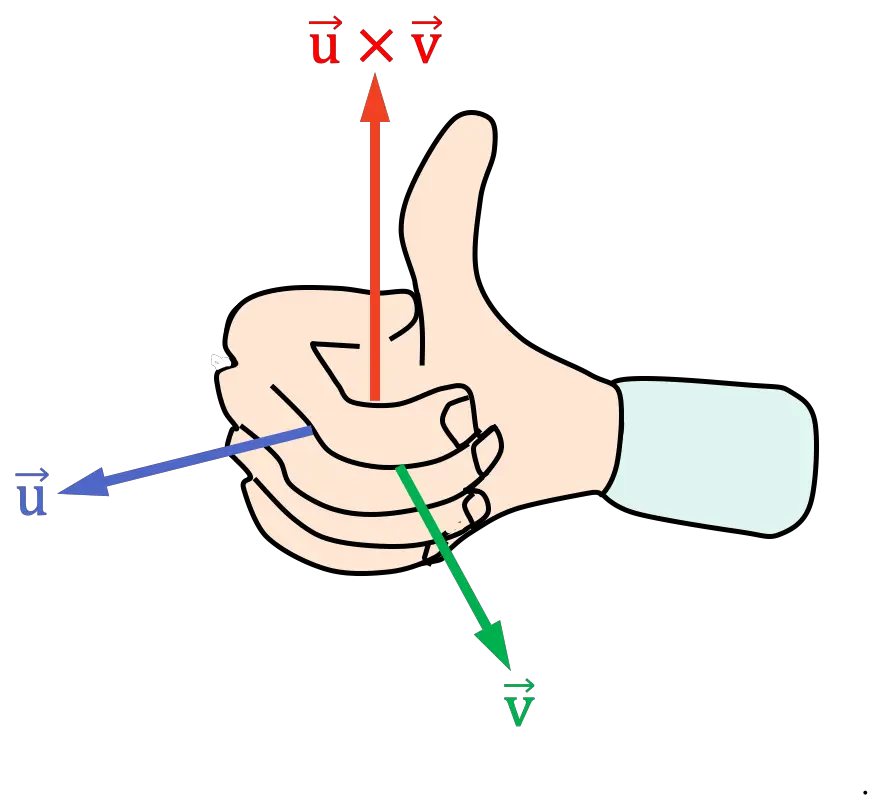
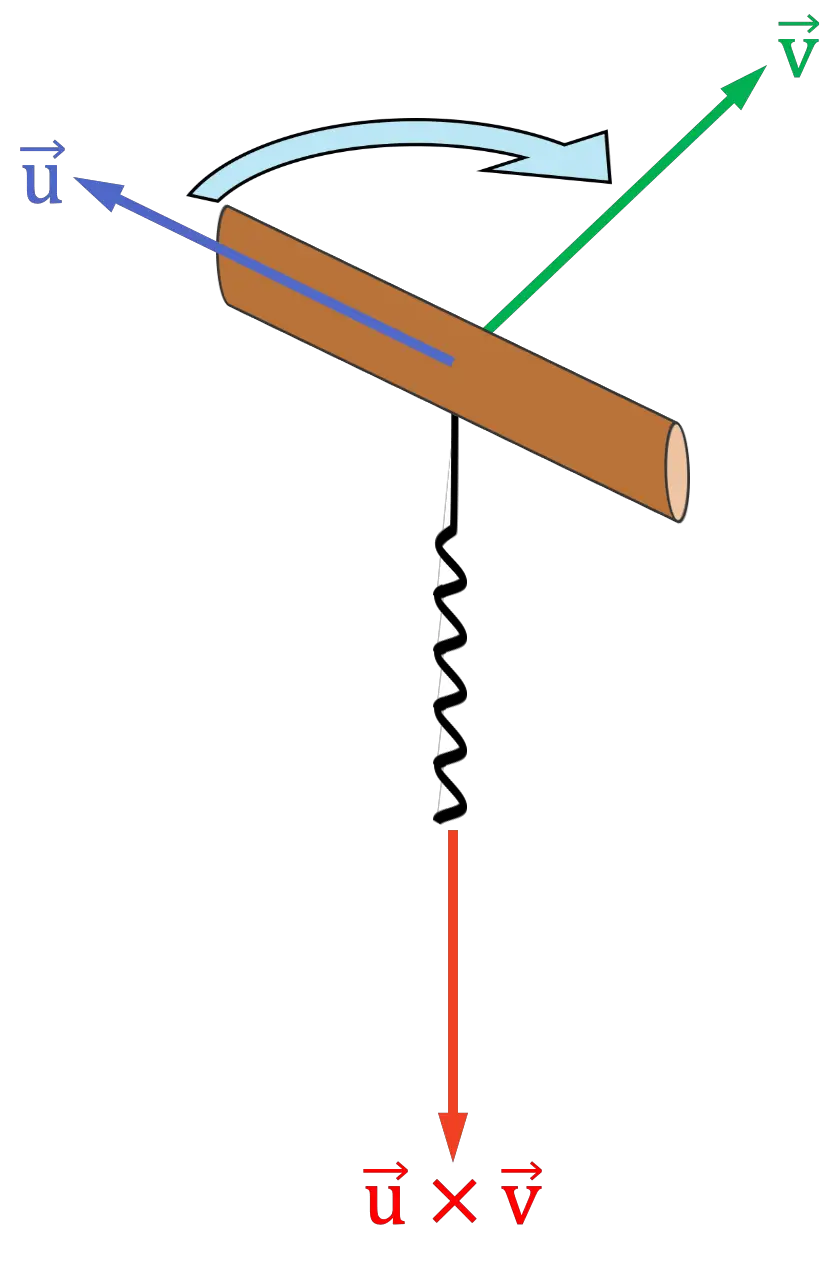
开瓶器规则

螺旋尺或螺旋尺类似于使用整个手掌的右手尺。程序如下：

发挥你的想象力，放置一个开瓶器（或螺钉），其手柄指向与叉积的第一个向量相同的方向。
$(\vv{\text{u}}).$
然后将开瓶器转向叉积的第二个向量
$(\vv{\text{v}})$

就好像你要把它放进软木塞里一样。您需要将开瓶器转到向量之间距离最短的一侧。
开瓶器螺旋指向的方向将是向量乘积的方向和方向
$(\vv{\text{u}}\times\vv{\text{v}}).$

两个向量叉积的性质

两个向量的叉积具有以下特征：

反交换性：向量积中涉及的向量的顺序并不是无关紧要的，因为符号根据它而变化。

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

关于向量加法和减法的分配律：

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

齐次性：将叉积的向量乘以标量（实数）相当于将叉积的结果乘以所述标量。

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

向量积产生的向量垂直于运算中涉及的两个向量。

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

此外，如果两个向量正交，则满足以下方程：

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

两个平行向量的叉积等于零向量（或零）。

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

如果我们不知道两个向量形成的角度，也可以使用以下表达式计算它们的向量乘积的模：

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

使用叉积计算平行四边形或三角形的面积

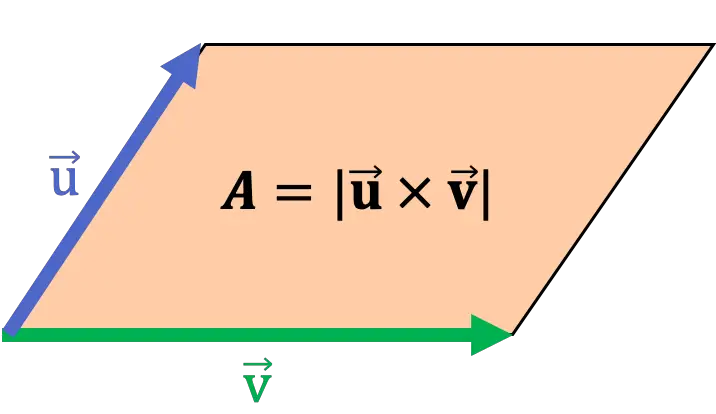
在几何上，两个向量叉积的模与以这两个向量为边的平行四边形的面积一致。因此，叉积可以用来计算平行四边形的面积。

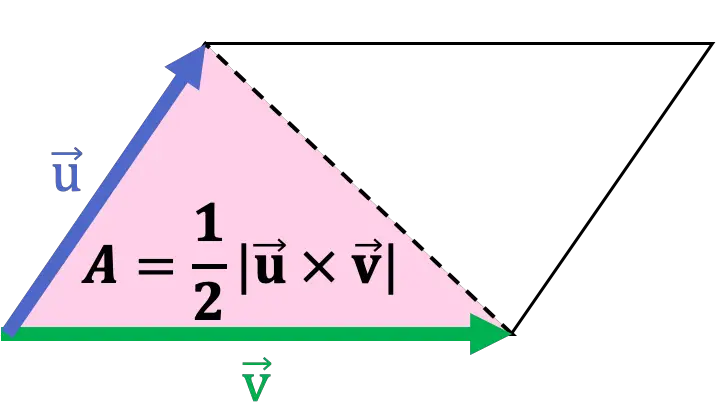
另外，平行四边形的对角线将其分成两个三角形，或者换句话说，三角形是平行四边形的一半。因此，三角形的面积是以它的两条边为向量的叉积的模数的一半。

回想一下，3 维空间中向量的模是其坐标平方和的根：

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

这是两个向量叉积在数学领域的两个应用。然而，它还有其他用途，例如在物理学中它用于计算磁场。

解决了向量的向量积的练习

练习1

计算以下两个向量之间的叉积：

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

查看解决方案

为了确定向量之间的向量积，我们必须求解以下维度为 3×3 的行列式：

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

在这种情况下，我们将通过佐剂或辅因子来求解行列式（但也可以使用萨勒斯规则）：

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

因此，两个向量的向量积的结果是：

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

练习2

求以下两个向量之间的叉积：

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

查看解决方案

为了找到两个向量之间的向量积，我们必须求解以下 3×3 行列式：

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

在这种情况下，我们将通过伴随或辅因子求解行列式（尽管萨鲁斯规则可以互换使用）：

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

因此，两个向量之间的向量积的结果是：

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

练习3

知道两个向量的模及其形成的角度：

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

确定两个向量叉积的大小。

查看解决方案

我们可以通过应用以下公式轻松计算两个向量之间的向量积的模：

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

练习4

来自屏幕平面中包含的以下向量：

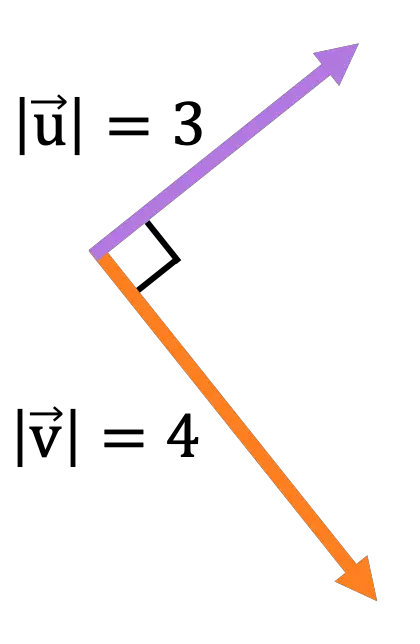
计算由以下向量运算产生的向量的大小、方向和方向：

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

查看解决方案

这两个向量是垂直的，因此向量积的范数为：

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

另一方面，矢量乘积得到的矢量垂直于参与运算的两个矢量，因此其方向将垂直于屏幕。

最后，使用直线（或螺旋）规则，我们可以推断出结果向量的方向将朝向屏幕内部。

练习5

计算以下列向量作为其两条边的平行四边形的面积：

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

查看解决方案

平行四边形的面积与形成它的向量叉积的模重合。因此，我们计算向量的向量积：

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

然后是你的模块：

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

练习6

求以下列点为顶点的三角形的面积：

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

查看解决方案

首先，我们必须计算形成三角形边的向量：

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

三角形的面积是构成它的向量的向量乘积的一半。因此，我们计算向量的向量积：

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

在你的模块之后：

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

最后，三角形的面积将是模块的一半：

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

两个向量的叉积（或叉积）

两个向量的叉积是多少？

计算两个向量叉积的公式