在这里您将了解存在哪些类型的不连续性。此外,您将能够看到所有类型的不连续性的示例,并且能够通过已解决的函数类型的不连续性练习进行练习。
什么是所有类型的不连续性?
不连续性分为三种类型,即:
- 可避免的不连续性:函数在一点处的横向极限与函数的值不重合。
- 不可避免的有限跳跃不连续性:函数在一点处的横向极限是不同的。
- 不可避免的无限跳跃不连续性:函数的横向极限之一给出无穷大或不存在。
为了完成对这些概念的理解,我们将更详细地解释每种类型的不连续性,并且我们将看到具有三种类型的不连续性的函数示例。
可避免的不连续性
可避免的不连续性是一种不连续性,如果该点存在边界但与函数的值不重合或函数的图像不存在,则该点具有函数。

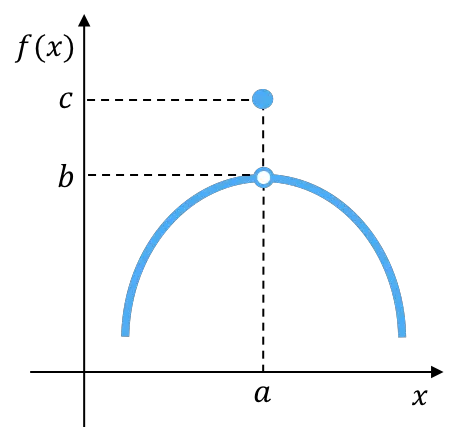
该函数的横向极限彼此相等,但与函数在该点的值不同。因此,该函数呈现出可避免的不连续性。
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
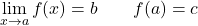
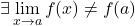

上例中的函数具有可避免的不连续性,因为 x=a 处的横向极限具有相同的值,但此时函数的图像不存在。
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
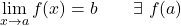
➤请参见:函数的横向极限
有限跳跃不可避免的不连续性
不可避免的有限跳跃不连续性是一种不连续性,当函数在该点的横向极限不相等时,该点呈现函数。
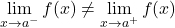
例如,下一个分段定义的函数在定义改变点处的横向极限是不同的,因此该函数在该点处具有不可避免的有限跳跃不连续性。
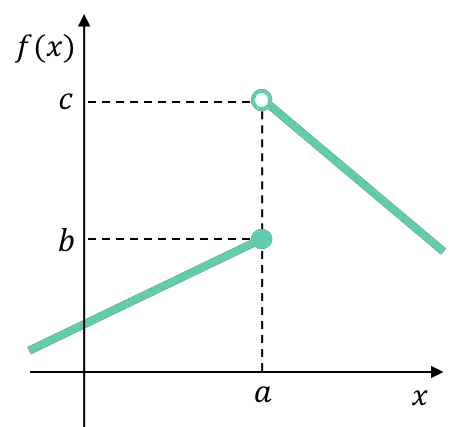

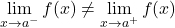
这种类型的不连续性通常出现在分段(或分段)定义的函数中。
➤请参阅:分段函数的连续性
无限跳跃 不可避免的不连续性
不可避免的无限跳跃不连续性是一种不连续性,如果该点的横向极限之一是无限的或不存在,有时它会起作用。

以下函数的左极限给出实数,但右极限给出无穷大。因此,该函数呈现出不可避免的无限跳跃不连续性。
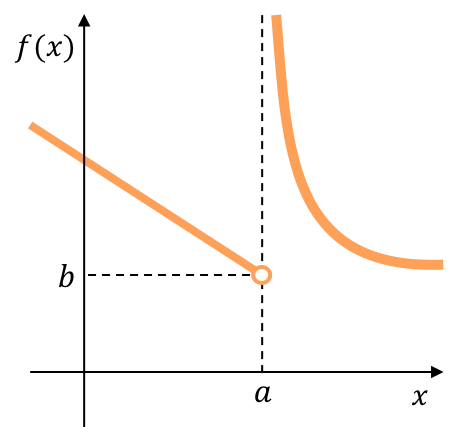
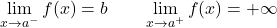
下面您可以看到一个图形函数,其两侧极限为无穷大,因此该函数具有不可避免的无限跳跃不连续性。


这种类型的不连续性通常发生在有理(或分数)函数中。
解决了有关不连续性类型的练习
练习1
确定以下分段函数在点 x=3 处的不连续类型:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”232″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-8185827ad36ab3921bb96eb5a6da21a9_l3.png)
查看解决方案
函数第一个元素的定义域,
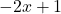
和第二段一样,
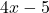
,都是实数,因为它们是多项式函数。
因此,函数可能不连续的唯一点是分段函数的停止点。因此,我们将在此阶段计算横向限制:
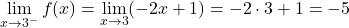
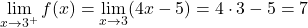
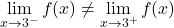
x=3 处的两个横向极限给出了不同的结果。因此,x=3点是不可避免的有限跳跃不连续点。
练习2
找出以下有理函数在不属于其定义域的点处呈现哪种类型的不连续性:
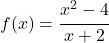
从逻辑上讲,要解决此练习,您必须首先找到函数的域。因此,由于这是一个有理函数,我们将分母设置为 0 并求解所得方程:
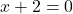
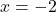
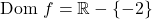
因此,除了 x=-2 之外,该函数在所有点上都是连续的,所以让我们看看 x=-2 点是什么类型的不连续性。为此,我们计算函数在该点的极限:
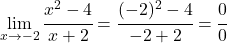
但是我们在零之间获得零不确定性,因此我们对分子和分母的多项式进行因式分解并简化:
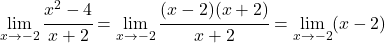
现在我们解决极限:
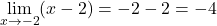
因此,函数在点 x=-2 处的极限确实存在并给出 -4。现在我们检查一下它是否存在
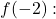
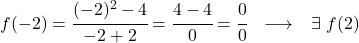
在计算函数的图像时,不定式0/0无法简化且无解。所以
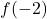
不存在。
总之,函数在 x=-2 处的极限存在,但是
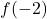
不会。因此,x=-2 是可以避免的不连续性。
练习3
分析以下有理函数的连续性:
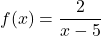
要判断它是否是连续函数,我们必须首先计算它的定义域。因此,我们将有理函数的分母设置为零,以查看哪些点不属于该域:
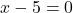
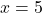
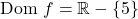
因此,除了 x=5 之外,该函数在所有点上都是连续的。那么我们通过计算此时的极限来看看 x=5 是什么类型的不连续:
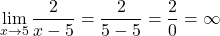
我们发现数字除以 0 具有不确定性。因此,我们计算函数在 x=5 处的横向极限:
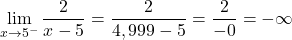
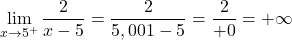
x=5 处函数的左极限给出负无穷大,右极限给出正无穷大。因此,该函数在 x = 5 处具有不可避免的无限跳跃不连续性,因为此时至少有一个横向极限趋于无穷大。
练习4
确定下图中所示分段函数的所有不连续点:
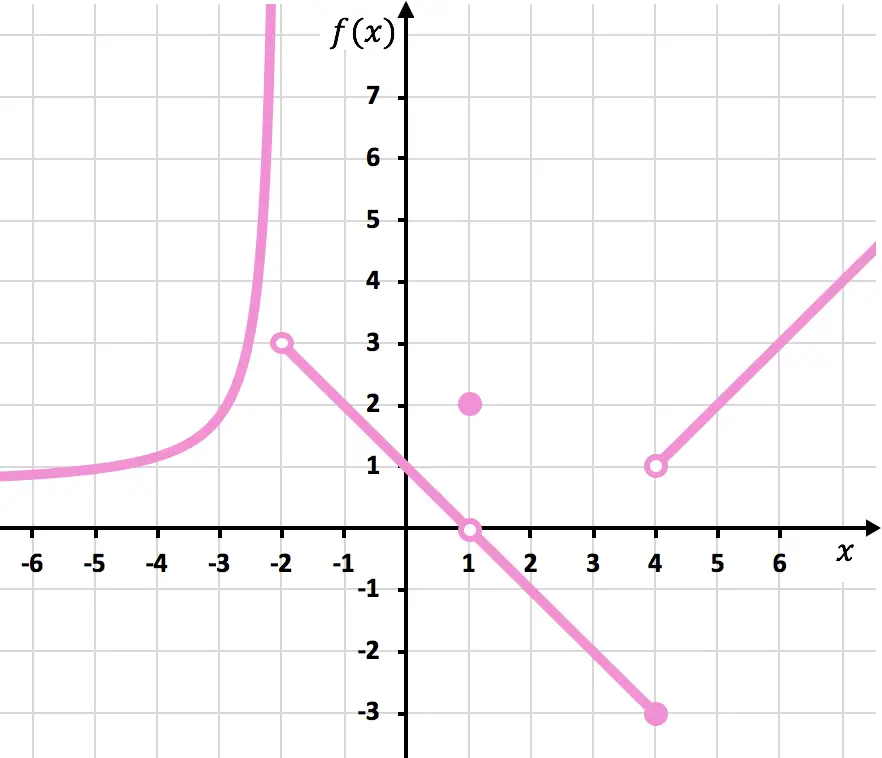
要绘制该函数,您必须在 x=-2、x=1 和 x=4 处举起铅笔。因此该函数在这三个点处是不连续的。
在 x=-2 处,左侧极限为 +∞,右侧极限为 3。因此,由于一侧极限为无穷大,因此该函数在 x=-2 处不可避免地存在无限跳跃不连续性。
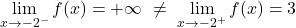
x=1 处函数的极限为 0,另一方面,x=1 处函数的值等于 2。因此,该函数在 x=1 处呈现可避免的不连续性。
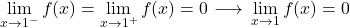
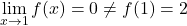
当 x = 4 时,左侧极限为 -3,右侧极限为 1。因此,由于两侧极限不同且均不给出无穷大,因此该函数在 x = 4 处不可避免地存在有限跳跃不连续性。
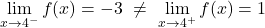
练习5
找出下图中表示的函数的所有渐近线和不连续点:
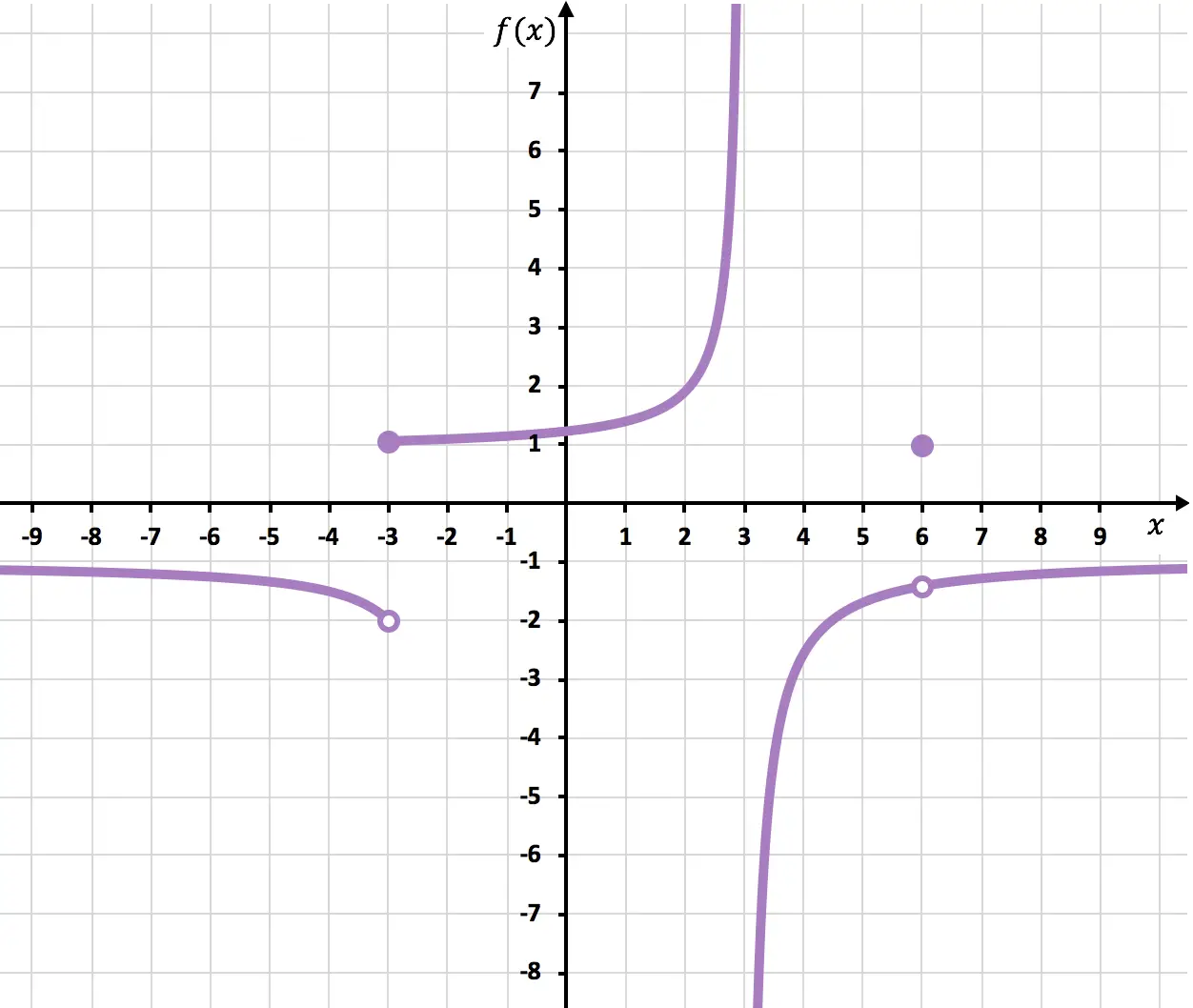
渐近线
该函数非常接近垂直线 x=3,但从未触及它。另外,x=3 处的左侧极限为+∞,右侧极限为-∞。因此,x=3 是垂直渐近线。

同样的情况也发生在水平线 y=-1 上,函数非常接近 y=-1,但从未穿过它。此外,当 x 接近 + 无穷大和 – 无穷大时,函数的极限为 -1。因此,y=-1 是水平渐近线。

不连续性
当 x=6 时,函数因存在开路点而中断。 x 接近 6 时的极限是 -1.4,但 f(6)=1。因此,该函数在 x=6 处具有可避免的不连续性,因为极限值与函数值不一致:
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)
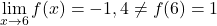
当 x=-3 时,横向极限不重合,并且没有给出无穷大。因此,该函数在 x=-3 处具有不可避免的有限跳跃不连续性。
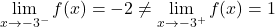
最后,该函数在 x = 3 处存在不可避免的无限跳跃不连续性,因为此时至少有一个横向极限会导致无穷大。

![]()

![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
![]()
![]()

![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
![]()
![]()

![]()
![]()
![]()

![]()

![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”232″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-8185827ad36ab3921bb96eb5a6da21a9_l3.png)


![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)