在本文中，我们将解释如何解决无穷负无穷 (∞-∞) 不确定性。您将找到具有不同类型函数的这种不确定性的示例，此外，您将能够通过逐步解决不确定性无限减无穷的练习进行练习。
解决不确定性无穷减无穷
当函数的极限给出无穷大减无穷大时，就意味着它是不定性（或不定形式）。也就是说，给出不确定性减去无穷大的函数的极限不能通过执行直接计算来确定，而是必须执行初步程序。
因此，要解决无穷减无穷的不确定性，我们必须首先应用取决于函数类型的程序：如果是多项式函数，则可以通过比较来计算，如果是有理函数，则必须将分数简化为公分母，如果是无理函数，则必须乘以共轭。
接下来，我们将通过示例了解在每种类型的函数中如何解决不确定性无穷大减去无穷大的问题。
多项式函数中的无穷减无穷不确定性
在多项式中，不确定性无穷大减去无穷大等于最高阶无穷大，即最高阶项决定无穷大的正号或负号。
例如，看看以下多项式函数的极限，它给出了不确定形式无穷大减去无穷大：
在这种情况下，项 x 2是二次项，项 3x 是一次项，因此单项式 x 2占主导地位，因为它是更高阶的。因此，极限的结果是从这项得到的无穷大。
看看这些其他例子：
![\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bfb5cd294a19de382f74738af6be724_l3.png "Rendered by QuickLaTeX.com")
简而言之，当我们对多项式函数 中的无穷大进行限制时，我们必须简单地将无穷大代入最高次项，而忽略所有其他项。
不确定性 无限减无穷 带分数
当代数分数的加法或减法中出现无穷大减无穷大的不确定性时，必须先进行分数的加法或减法，然后计算极限。
让我们通过逐步求解示例来了解如何计算带分数函数中的不确定性无穷大减去无穷大：
我们先尝试计算极限：
但我们得到了不确定性 ∞-∞。
所以首先我们需要进行分数减法。为此，我们将分数简化为一个公分母，即将一个分数的分子和分母乘以另一个分数的分母：
![\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68e489c5833478cb20929ea07ae2971d_l3.png "Rendered by QuickLaTeX.com")
现在两个分数具有相同的分母，我们可以将它们合并为一个分数：
我们用分子和分母进行运算：
最后，我们再次计算极限：
在这种情况下，无穷大之间的无限不确定性给出+∞，因为分子的次数大于分母的次数。
➤看： 无穷大之间的无穷大是什么？
不确定性 无限减无穷 有根
当根式加法或根式减法中出现无穷大减无穷大的不确定性时，必须先将函数乘以和除以共轭根式表达式，然后求解极限。
我们将通过逐步示例了解如何求解无理函数中的不确定性无穷大减无穷大：
我们首先尝试解决带有根式的函数的极限：
然而，我们得到了不定形式 ∞-∞。因此，要知道无穷大减去无穷大有多少不确定性，我们需要应用所解释的过程。
由于函数有根式，我们将整个函数乘以和除以共轭无理表达式：
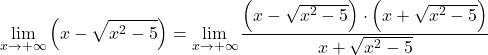
分子的代数表达式对应于和与差的乘积的显着恒等式，因此我们可以简化该表达式：
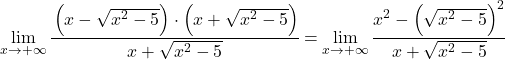
现在我们简化极限的根，因为它是平方的：
我们对分数的分子进行运算：
最后，我们重新计算极限：
因此极限的结果是 0，因为任何数字除以无穷大都等于 0。
解决了无穷负无穷不确定性问题
练习1
当 x 接近无穷大时，求解以下极限：
在这个极限中，最高阶项是三次，所以我们关注从这项得到的无穷大。
练习2
当 x 接近负无穷大时，计算以下多项式函数的极限：
负无穷大的立方仍为负，但平方后变为正。后来虽然他们的符号被前面的系数修改了：
![\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-172f2927f65e61079b13abd02234f1c7_l3.png "Rendered by QuickLaTeX.com")
然后，不定形式无穷大减无穷大由最高阶项 (-5x 3 ) 定义，从中我们获得正无穷大：
练习3
确定以下有理函数的无穷大极限：
首先，我们尝试通过替换函数中的无穷大来计算极限：
但我们最终得到不确定性 ∞ – ∞。因此，我们将分数减少到一个公分母：
![\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e2820674bc86d085f6deec7fdf9adf8_l3.png "Rendered by QuickLaTeX.com")
由于两个分数现在具有相同的分母，我们可以将它们合并为一个分数：
我们把分子放在括号里：
最后，我们确定限制：
在这种情况下，不确定性 ∞/∞ 给出 +∞，因为分子的次数大于分母的次数。
练习4
当 x 接近 0 时，求解以下分数函数的极限：
我们首先像往常一样尝试计算极限：
但我们得到了不定形式 ∞-∞。因此，我们需要将函数的分数减少到一个公分母。
在这种情况下， x 4是 x 2的倍数，因此只需将第二个分数的分子和分母乘以 x 2我们将得到两个分数具有相同的分母：
![\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-876115dc1fb49e81373d70be5fdcfb5e_l3.png "Rendered by QuickLaTeX.com")
我们现在可以减去两个分数：
我们再次尝试解决限制：
但我们最终得到了常数除以零的不确定性。因此有必要计算函数的横向极限。
总之，由于函数在点 x=0 处的两个横向极限为 -∞，因此该极限的解为 -∞：
练习5
求解以下有根函数的无穷大极限：
尝试求解极限，我们得到不确定性无穷大减去无穷大：
因此，由于函数中有根式，我们需要将其乘以和除以共轭根式表达式：
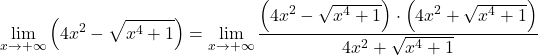
在分子中，我们有一个和与差的显着乘积，它等于平方差。然而：
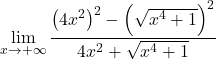
我们将根式简化为平方：
我们用分子来运算：
最后，我们找到极限：
在这种情况下，无限不确定性除以无穷大更加无限，因为分子的次数大于分母的次数（回想一下，平方根将次数减少了二：
）。
练习6
当 x 接近无穷大时，求解以下无理函数的极限：
首先，我们尝试照常计算极限：
但它最终给我们带来了无穷大之差的不确定性。因此，由于函数有根，我们需要将表达式与共轭根式相乘和相除：
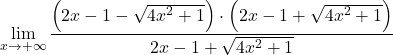
我们将分数分子的显着相等性分组：
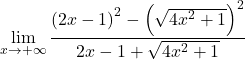
我们求解平方根：
我们求解差平方的显着恒等式：
我们用分子来运算：
最后，我们计算无穷大的极限值：
尽管分母中有一个 x 平方，但它的次数实际上是 1，因为它位于根内部：
因此，由于分子的次数与分母的次数相同，因此不确定性-∞/+∞的结果是较高次数x的系数的除法。
请注意，由于分母中有两个一级项
和
，为了解决不确定性-∞/+∞，需要取一次项的所有系数，也就是说
的
和
的
练习7
计算当 x 接近以下带有分数的函数的 1 时的极限：
尝试求极限，我们得到无穷大减去无穷大的不确定极限：
因此，我们必须将分数化简为一个公分母，或者换句话说，我们必须将一个分数的分子和分母乘以另一个分数的分母：
![\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-75bf3ffa177f32711c5509ce5fe5992d_l3.png "Rendered by QuickLaTeX.com")
由于这两个分数现在具有相同的分母，我们可以将它们放在一起：
我们经营：
我们再次尝试解决极限：
但我们发现不确定性为零除以零。因此，我们必须对分子和分母多项式进行因式分解：
现在我们通过删除分子和分母中重复的因子来简化分数：
最后，我们解决了限制：
