在此页面上，您将了解什么是三角矩阵以及不同类型的三角矩阵以及示例。此外，您还将了解如何计算三角矩阵的行列式以及这个非常有趣的矩阵的属性是什么。最后，我们还解释一下什么是 Hessenberg 矩阵，因为它是与三角矩阵相关的矩阵。
什么是三角矩阵？
三角矩阵的定义：
三角矩阵是一种方阵，其中主对角线上方或下方的所有元素均为零 (0)。
三角矩阵广泛用于线性代数计算，因为用这种类型的矩阵求逆三角矩阵、计算其行列式、甚至求解线性方程组都比使用所有位置上元素均不为 0 的矩阵容易得多。 。
上三角矩阵
上三角矩阵是主对角线以下元素为零（0）的方阵。
上三角矩阵示例：
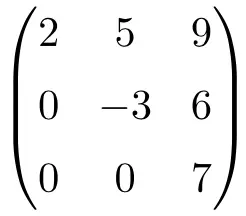
下三角矩阵
下三角矩阵是一个方阵，主对角线上方的每个元素都有一个零 (0)。
下三角矩阵的示例：
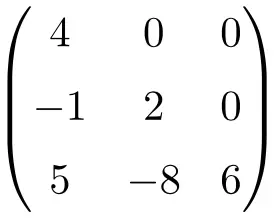
有时，这些矩阵也用字母 U 表示上三角矩阵，用字母 L 表示下三角矩阵。虽然这个命名法主要用在英语中，但实际上 U 代表上三角矩阵，L 代表下三角矩阵。
三角矩阵的示例
2 × 2 维三角矩阵
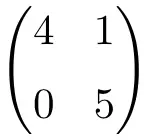
3×3 阶三角矩阵
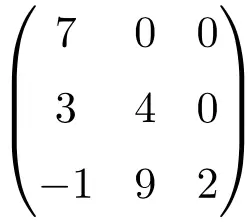
大小为 4×4 的三角矩阵
三角矩阵的行列式
三角矩阵 的行列式，无论是上三角矩阵还是下三角矩阵，都是主对角线上元素的乘积。
看一下下面的练习，它解决了如何计算三角矩阵主对角线元素的乘法来找到其行列式：
![\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7503e88c4eaabd74347a4f79461a3ebe_l3.png "Rendered by QuickLaTeX.com")
这个定理很容易证明：只需通过块（或辅因子）计算三角矩阵的行列式。下面使用通用三角矩阵详细介绍了该演示：
![\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91281c322af35f07cfbfd6fe61fc3c58_l3.png "Rendered by QuickLaTeX.com")
另一方面，我们知道，如果一个矩阵的行列式不为0，则它是可逆的。因此，如果主对角线上没有元素为0，则三角矩阵也将是可逆的，因此，它将是一个正则矩阵矩阵。
三角矩阵的性质
现在让我们看看三角矩阵有什么性质：
- 两个上三角矩阵的乘积等于一个上三角矩阵。反之亦然：两个下三角矩阵相乘得到另一个下三角矩阵。
![\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfd46e0ab8070d1c4c544d384fcf0f84_l3.png "Rendered by QuickLaTeX.com")
- 上三角矩阵的转置是下三角矩阵，反之亦然：下三角矩阵的转置是上三角矩阵。
![\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ca1b4a07e3136aa75d1a8026e5e7c1ae_l3.png "Rendered by QuickLaTeX.com")
- 如果三角矩阵主对角线上的所有元素都非零，即不为零，则该三角矩阵是可逆的。在这种情况下，上（下）三角矩阵的逆也是上（下）三角矩阵。
![\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-adafaa535a161d29c9bcb8a31a572dc2_l3.png "Rendered by QuickLaTeX.com")
此外，逆矩阵的主对角线将始终包含原始三角矩阵主对角线的元素的逆。
- 任何对角矩阵既是上三角矩阵又是下三角矩阵，例如：
![\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-497726e030cc2af2c07b16fdf3544024_l3.png "Rendered by QuickLaTeX.com")
- 所以标量矩阵也是一个上三角矩阵和下三角矩阵。例如单位矩阵：
![\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png "Rendered by QuickLaTeX.com")
- 显然，零矩阵也是一个上下三角矩阵，因为主对角线上方和下方的元素均为0：
![\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png "Rendered by QuickLaTeX.com")
- 三角矩阵的特征值（或特征值）是主对角线的元素。
![\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5](https://mathority.org/wp-content/ql-cache/quicklatex.com-272d0e156e1f27c20348b171c984e390_l3.png "Rendered by QuickLaTeX.com")
- 上三角矩阵或下三角矩阵始终能够在特征向量（或特征向量）的基础上进行对角化。
- 任何矩阵都可以分解为下三角矩阵和上三角矩阵的乘积。即任意矩阵都可以转化为三角矩阵乘法。此外，如果矩阵是可逆的，则这种变换是唯一的。为了对矩阵进行因式分解，通常使用 LU 分解方法。
将矩阵三角化
有几个关于可以通过改变底数来三角化的矩阵的定理。然而，在这里我们将看到如何通过对线 进行初等变换来对矩阵进行三角剖分，如高斯方法一样。
例如：
![\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f66a4f370b37168439de204c1b0b401c_l3.png "Rendered by QuickLaTeX.com")
这样，我们就已经对原始矩阵进行了三角化。
回想一下，高斯方法中线之间授权的基本变换是：
- 将一条线替换为其他线的线性组合。
- 将一行中的所有项乘以或除以 0 以外的数字。
- 编辑订单行。
海森伯格矩阵
Hessenberg矩阵的定义如下：
Hessenberg矩阵是一个“几乎”三角矩阵，也就是说从第一个下对角线（上Hessenberg矩阵）或第一个上对角线（下Hessenberg矩阵）开始，它的所有元素都为零。
我确信通过上 Hessenberg 矩阵示例和另一个下 Hessenberg 矩阵示例可以最好地理解它：
上赫森伯格矩阵
![\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e76ad0fae8a28b5e5f31535683e63df5_l3.png "Rendered by QuickLaTeX.com")
下赫森伯格矩阵
![\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9b13730483eaf930193baeb953d1d3c_l3.png "Rendered by QuickLaTeX.com")
既是上Hessenberg矩阵又是下Hessenberg矩阵的矩阵是三对角矩阵。
这个矩阵以20世纪德国著名工程师和数学家Karl Hessenberg的名字命名。
最后，这种类型的矩阵有一个特殊性，如果它乘以三角矩阵，结果总是Hessenberg矩阵。