角度的三角比是从直角三角形的三条边获得的比率。换句话说,这些是使用商(除法)比较其三边而得到的值。但需要注意的是,这些原因只存在于直角三角形(角为 90° 的三角形)中。
直角三角形中的三角比
六个最重要的三角比是:正弦、余弦、正切、余割、正割和余切。接下来,我们将详细解释如何定义这些原因,并讨论表征它们的公式。为了理解以下解释,我们将考虑以下直角三角形:

胸部
角度(sin 或 sin)的正弦值等于对边 a 与斜边 c 的商,因此,正弦公式为: sin (α) = a / c 。了解正弦的定义非常重要,因为它是所有三角学的基础,以及我们将在本节中介绍的其他原因。
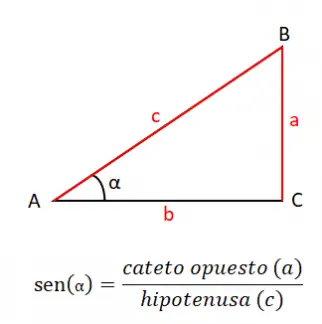
特拉夫根据正弦定理,我们可以计算三角形的任何一条边,我们可以通过连接其相应边之间某个角度的商来实现这一点。例如,如果我们要计算边a,并且我们有角度A和B的边值,我们可以使用公式: a / sin (A) = b / sin (B) 。通过求解这个简单的方程,我们得到了与我们想要计算的变量相对应的值。
余弦
角度的余弦(cos)等于相邻边(b)与斜边(c)的商,因此,余弦公式为: cos(α)= b / c 。在本例中,该公式由与我们要研究的角度(在本例中为角度 A 或 α)相接触的三角形的两条边组成。
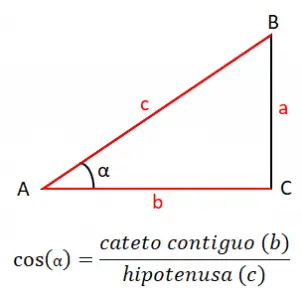
有了余弦,我们还有一种方法来计算三角形的边,这来自于余弦定理。这使我们能够将边与角连接起来,并给出以下三个表达式:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
切线
第三个最重要的原因是切线(tan 或 tg),我们将用它来结束原始原因集。这是通过将相对边 (a) 和相邻边 (b) 相除来计算的,因此正切公式为: tan (α) = a / b 。您可以在下面以图形方式查看它:
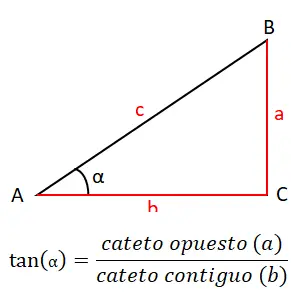
正切也有自己的定理,称为正切定理。这使我们能够将三角形两条边的长度与角的正切联系起来。陈述如下:“两条边相减所得的商等于与这两条边相对的两个角的平均值的正切与这些边之差的一半的正切之间的商”。
导出的三角比率
从我们刚才讨论的三个三角比,我们可以得到其他导出的三角比。这些是通过取正弦、余弦和正切的反比来获得的。
- 余割:是正弦的反比,计算公式为:cosec (α) = c / a 和 cosec (α) = 1 / sin (α)。
- 正割:是余弦的反比,计算公式为:sec (α) = c / b 和 sec (α) = 1 / cos (α)。
- 余切:是正切的反比,计算公式为:cotg (α) = b / a 和 cotg (α) = 1 / tan (α)。
三角比率表
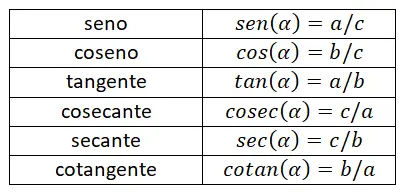
您可以在下面看到一个表格,其中总结了迄今为止解释的所有原因。有了这张表,您将能够有效地记住所有公式,因为它可以让您轻松区分每个数学表达式之间的差异。
圆内的三角比
研究三角学的另一种方法是通过测角圆周或单位圆,该圆周的半径等于 1,其原点是点 (0, 0)。该图由一个圆和圆内描绘的直角三角形组成,更准确地说,我们要研究的角度必须与原点相接触。
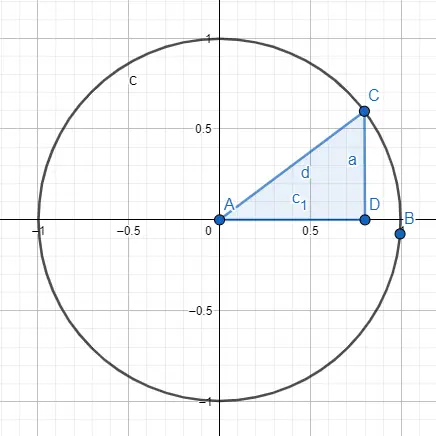
当我们有了这张图像时,我们知道半径等于斜边,即等于1。因此,如果我们要计算正弦和余弦,我们将使用半径的值和其他边的值三角形。为了计算正弦,我们将进行以下计算: sin (A) = CD / AC = CD / radius = CD / 1 = CD ,因此 A 的正弦为 a。另一方面,要计算余弦,我们将进行以下计算: cos (A) = AD / AC = AD / radius = AD / 1 = AD ,因此 A 的余弦为 c1。
记住两件事非常重要。首先,在三角比的研究中使用这个圆是因为需要处理比三角形可以研究的角度更大的角度。例如,150°的角不能通过简单的三角形来研究,因为它太大了。第二个要记住的事情是,正弦和余弦永远不能采用大于 1 且小于 -1 的值。
三角比率的符号
正如我们之前所说,为了处理大于三角形允许我们处理的角度,我们使用测角周长。为此,我们在划分圆周的四个象限之一中准确地表示圆内的三角形,在下图中您可以看到所表示的四个象限。
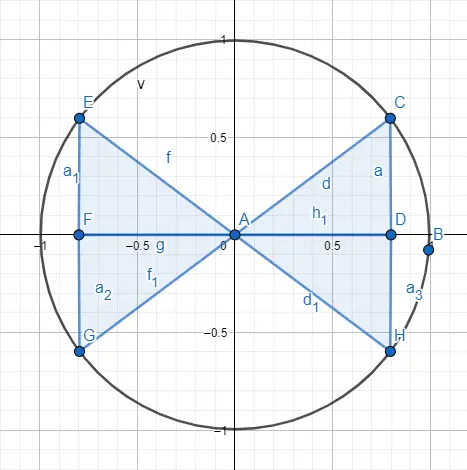
因此,要区分 30 度角和 210 度角,它们变得相同关于三角形内的分布,我们将根据三角形所在的象限使用符号分布。下面您可以看到每个象限对应的标志和绘制的示例。
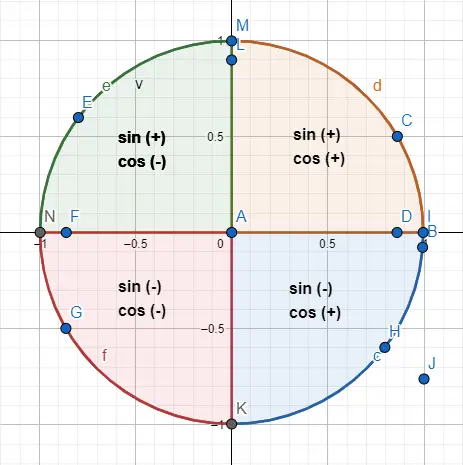
例如,角度 30° 和 210° 具有相同的数值,但它们的正弦和余弦具有相反的符号。因此:sin(30) = 1/2 且 cos(30) = √3/2,而 sin(210) = -1/2 且 cos(210) = -√3/2。为了达到这个结果,我们在圆周上表示两个角度(下图),并遵循符号的指示。
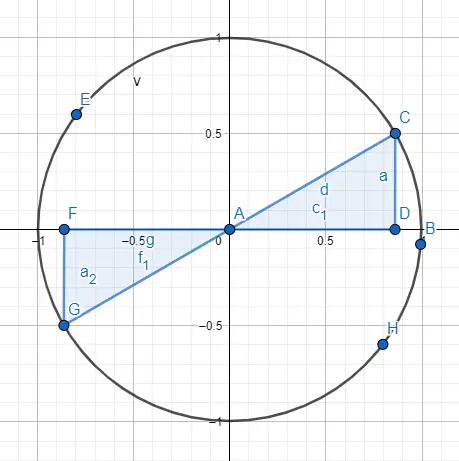
最后,如何可以有大于 360° 的角度,尽管看起来可能不像,因为圆周只有 360°。但是,如果我们想要求解 750° 的角度,我们可以减少到 0° 到 360° 之间的角度。只需将 750° 除以 360,余数就是剩余的角度,在 750° 的情况下,我们得到 30° 的角度。
角度类型取决于象限
不同角度之间存在关系,这使我们能够计算比率属于圆的所有角度的三角值。让我们了解这些原因减少到第一象限。这意味着我们从某个角度到第一象限进行简化,然后应用相应的符号。下面您将找到不同程序的解释(取决于象限):
第一象限
在第一个象限(0° – 90°)中,我们只需用给定的角度求解三角比即可。如果我们看一下我们之前解释过的符号的图片,正弦和余弦前面都有一个正值(我们得到的结果不会受到符号的影响)。
从第二象限减少到第一象限
在第二象限 (90° – 180°)中,我们处理补角,这意味着两个角度之和为 180°。因此,我们需要从第二象限减少到第一象限,我们用公式 180 – α = β来完成,其中 α 是第一象限的角度, β是原始角度。
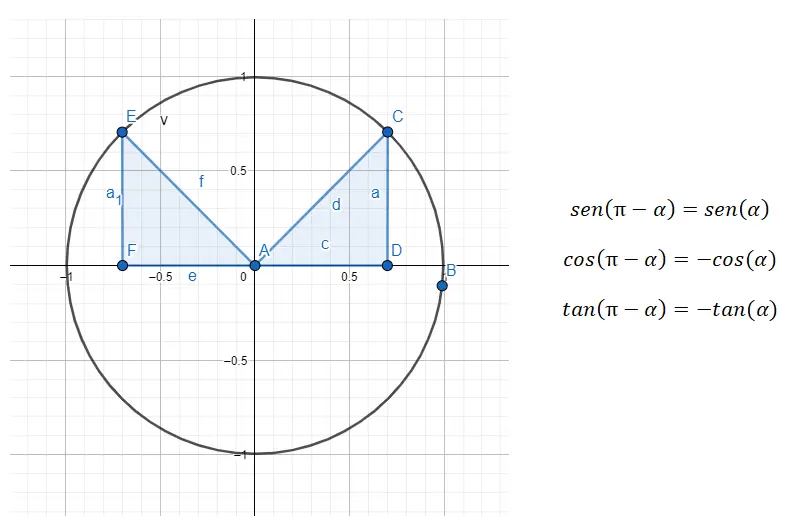
例如,如果给定角度 135°(属于第二象限),我们需要首先找到与此相关的第一象限的角度。在此示例中,我们要查找的角度 (α) 为 45°,因为 180 – 45 = 135。因此,这将是正确的:sin (135) = sin (180 – 45) = sin (45), cos (135 ) = cos (180 – 45) = -cos (45) 且 tan (135) = tan (180 – 45) = -tan (45)。
将第三象限缩小到第一象限
在第三象限 (180° – 270°)中,我们处理相差 80° 的角度,这意味着角度相距 180°。所以如果我们想从第三象限减少到第一象限,我们需要使用公式 180 + α = β ,其中 α 是第一象限的角度, β是原始角度。
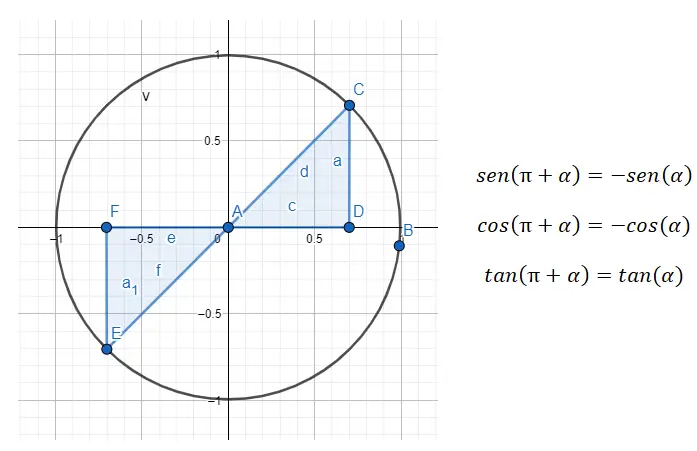
例如,如果给定角度 225°(属于第三象限),我们需要找到与其对应的第一象限的角度。在 225° 的情况下,我们要查找的角度 (α) 又是 45°,因为 180 + 45 = 225。因此,sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) 且 tan (225) = tan (180 + 45) = tan (45) 将得到满足。 )。
将第四象限缩小到第一象限
在第四象限(270° – 360°),我们处理相反的角度,这意味着角度在数值上相等,但符号相反,例如 30° 和 -30°(相当于 330°,因为 360° – 30° = 330°) 。重要的是要记住,对角可以写为正角和负角或两个正角(在我们刚刚讨论的示例中,我们解释了差异)。
因此,如果我们想要从第四象限减少到第一象限,我们需要使用公式 360 – α = β ,其中 α 是第一象限的角度, β是原始角度。
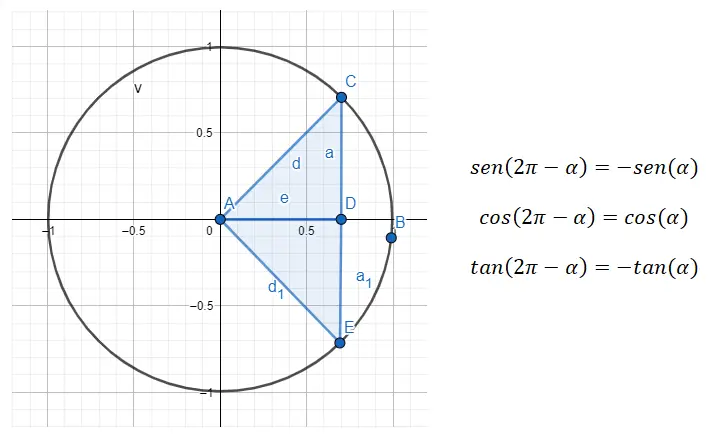
例如,如果给定角度 315°(属于第四象限),我们需要首先找到与此相关的第一象限的角度。对于我们正在寻找的角度 (α),它仍然是 45°,因为 360 – 45 = 315。因此,sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) 且 tan (315) = tan (360 – 45) = -tan (45)。总之,我们已经看到了从所有象限的 45° 导出的角度。
最重要角度的三角比
有许多角度,称为显角,在三角学中最常见。强烈建议熟记三角比率。因此,下面我们创建了一个表格,其中包含这些角度及其导数的三角比(相同的角度,但相差 90、180 或 270 度):
| 角度(°) | 角度(弧度) | 胸部 | 余弦 | 切线 |
| 0° | 0 拉德 | 0 | 1 | 0 |
| 30度 | 1/6π弧度 | 1/2 | √3/2 | √3/3 |
| 45° | 1/4π弧度 | √2/2 | √2/2 | 1 |
| 60° | 1/3π弧度 | √3/2 | 1/2 | √3 |
| 90° | 1/2πrad | 1 | 0 | 无穷大 |
| 120度 | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135° | 3/4π弧度 | √2/2 | -√2/2 | -1 |
| 150度 | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180° | π弧度 | 0 | -1 | 0 |
| 225° | 5/4π弧度 | -√2/2 | -√2/2 | 1 |
| 270度 | 3/2πrad | -1 | 0 | 无穷大 |
| 315° | 7/4π弧度 | -√2/2 | √2/2 | -1 |
三角比之间的关系
有多种方法可以关联不同的三角比率。从这些关系中,我们获得了不同三角函数之间的一种等式,我们称之为三角恒等式。由于这种类型的身份,我们可以根据任何其他身份来计算比率。应该注意的是,三角恒等式有许多不同类型,它们是根据支持表达式本身的关系类型进行分类的。
三角比解决的问题
接下来,我们为您提供一系列练习,您可以将本文中解释的所有理论付诸实践。请记住,如果您在任何时候遇到困难或有疑问,您可以重读这篇文章,并且通过第二次阅读,您肯定会更好地理解所有内容。也就是说,你可以开始练习:
练习1
计算 225° 的六个三角比:
我们首先计算角度 (α),它等于:180 + α = 225°,因此 α = 45°。
正弦(225) = 正弦(180 + 45) = -正弦(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
tan(225) = tan(180 + 45) = tan(45) = 1
练习2
计算 120° 角的六个三角比:
我们首先计算角度 (α),它等于:180 – α = 120°,因此 α = 60°。
正弦(120) = 正弦(180 – 60) = 正弦(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
练习3
计算 510° 角的六个三角比:
开始之前,必须减少角度:510 / 360 = 1 圈,剩余角度为 150。接下来,我们计算角度 (α),它等于:180 – α = 150,因此 α = 30°。
正弦(150) = 正弦(180 – 30) = 正弦(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3