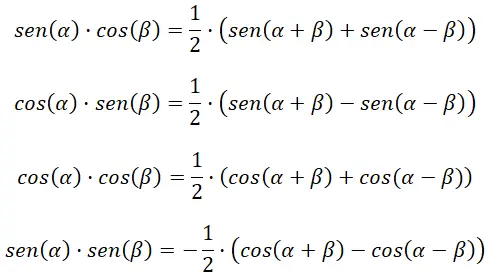三角恒等式是不同三角函数之间的等式。由于这些三角等价,我们可以根据任何其他三角比推导出某个三角比。因此,为了理解三角恒等式的公式,有必要知道这些比率的公式。如果您不知道您的情况,我们建议您访问最后一个链接。
三角恒等式表
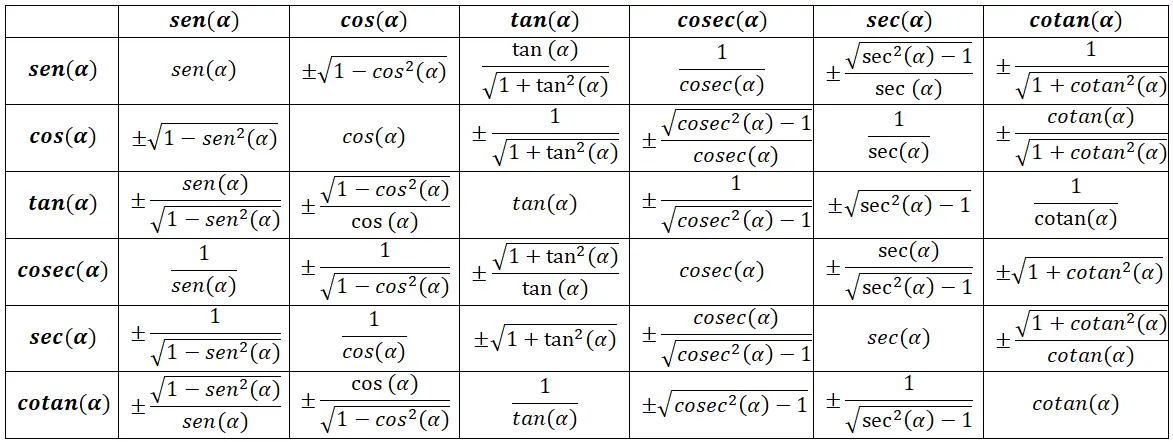
基本三角恒等式
有一系列基本三角恒等式被认为是最重要的,因为它们为其他三角恒等式提供了理论基础。这些是最常见的,也可能是最容易记住的,因为它们非常直观。请记住,所有公式都将基于下图:

基本三角恒等式
第一个恒等式是所谓的基本三角恒等式,也称为正弦和余弦之间的关系。下面是其数学证明:sin² (α) + cos² (α) = 1。
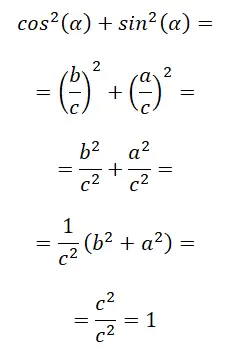
在最后一步中,我们基本上应用毕达哥拉斯定理,因为 c² = a² + b²,所以我们剩下 c² / c² 等于 1。总之,我们可以说: sin² (α) + cos² (α) = 1。
割线和正切的关系(割线平方)
其次,我们有一个将正切与正切联系起来的三角恒等式,其表达式如下: sec² (α) = 1 + tan² (α) 。在下图中,您可以看到一些构成此恒等式的提醒公式,以及得出最终公式所需遵循的过程:
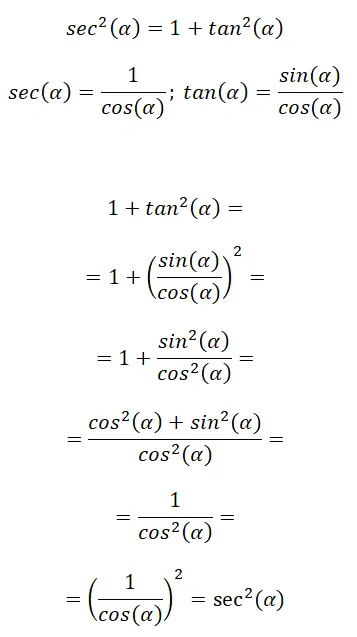
在这种情况下,我们使用三角比率公式来查找其他比率。总之,我们可以说:sec²(α) = 1 + tan²(α)。
余割和余切之间的关系(余割平方)
从余割和余切的定义我们可以找到正切公式的联系,由此我们可以推导出另一个三角恒等式: cosec² (α) = 1 + cotg² (α) 。
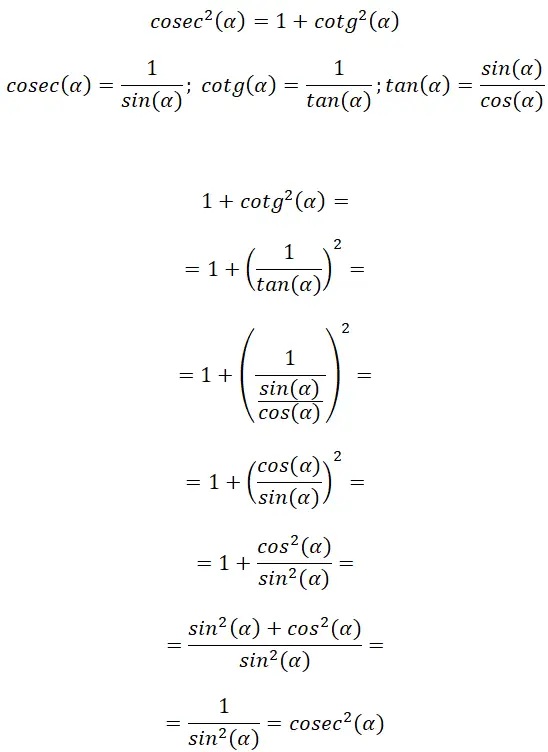
通过这个演示,我们可以验证:cosec² (α) = 1 + cotg² (α)。此外,我们可以看到这种关系与前一种关系有一些相似之处,这是由于正切和余切之间的相似性。
和角与减角的三角比
角和或角减比是通过计算两个角度相加或相减的三角比而获得的一种恒等式。例如,如果我们要计算 90 + 60 的正弦,有一系列公式可以使这个计算变得更容易。下面列出了这种类型的三角恒等式的所有公式:
角度和的正弦: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
角度减法的正弦:sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
角度和的余弦: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
角余弦减法: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
角度和的正切: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
角正切减法: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
显然,计算 150° 的正弦比使用我们刚才解释的公式计算 (90° + 60°) 的正弦要容易。那么为什么这些公式很重要呢?答案是,这些恒等式使我们能够从更简单的角度计算复杂角度的三角比。因此,如果我们记住了值得注意的(最相关的)角度的比率,我们就不需要使用计算器来计算更复杂的角度(例如 150°)的比率。
双角三角比
当我们想要计算双角 (2α) 的三角比时,我们可以通过一系列恒等式来实现。更准确地说,我们可以通过与上一节讨论的公式非常相似的公式来做到这一点。因为,如果我们将β更改为 α,则在前面的表达式中,我们剩下 (α + α),这相当于 (2α)。考虑到这一点,我们可以得出以下恒等式:
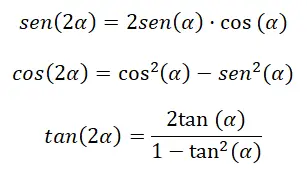
您可以看到下面的演示:
双角的正弦:sin(2α)=sin(α)cos(α)+cos(α)sin(α)=2sin(α)cos(α)
双角余弦: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
双切线角: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
半角的三角比
此外,还有一些恒等式可以让我们计算半角的三角比 (α/2) :
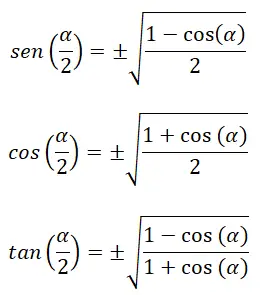
以下是已知的公式:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
如果我们使β = α/2,那么我们可以通过将正弦情况下的两个表达式相减,在余弦情况下将它们相加,然后将得到的两个公式(正弦公式和余弦公式)相除来证明这些恒等式在切线的情况下。然而,仍然需要在下面获得的公式中分离出我们想要计算的比率:
半正弦角:1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
半角余弦:1+cos(α)=2cos²(α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
三角的三角比
在具有三角(3α)的情况下,我们还可以使用某些恒等式来计算它们的三角比。这些恒等式来自以下已经解释过的公式:双角恒等式、和角恒等式以及三角学的基本恒等式。
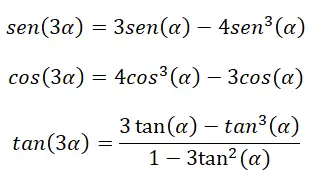
为了证明这些恒等式,我们必须使用角和公式:
角度和的正弦:sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
角度和的余弦: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
因此,如果我们应用刚才讨论的表达式中的双角公式并应用三角学的基本恒等式,我们就可以证明恒等式。值得一提的是,使用基本三角恒等式允许我们将表达式中的所有比率转换为一个。这就是为什么三角的正弦公式仅由正弦组成,而余弦的公式仅包含余弦。下面您可以看到完整的过程:
三角的正弦:sin(3α)=sin(α+2α)=sin(α)cos(2α)+sin(2α)cos(α)=
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin3 (α) – sin3 (α) + 2 sin (α) – 2 sin3 (α) =
= 3 sin (α) – 4 sin³ (α)
三角余弦: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos3 (α) – 3 cos (α) + 3 cos3 (α) =
= 4 cos³ (α) – 3 cos (α)
最后,三角的正切可以通过两种方式计算:第一种是将正弦公式除以余弦公式,第二种是将三角的正切表达式代入以下公式来计算和角:tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α))。
根据角度类型的三角恒等式
对一系列公式进行评论很重要,这些公式在某种程度上是允许直接快速计算三角比率的规则。事实上,它们也可以被认为是三角恒等式,因为它们与我们刚才讨论的所有表达式具有相同的特征。更准确地说,这些公式使我们能够根据一个角度与另一个角度的关系来确定该角度的三角关系。
互补角
互补角(α 和β )的总和等于 90°,因此当我们将它们相加时,我们会得到一个直角。要确定α是β的余角,我们必须解一个非常简单的方程:α = 90 – β ,如果这个等价的结果一致,那么我们就可以断定它们是互补的。由于这些恒等式,我们可以推导出一个角度与另一个角度的三角比。
余角的正弦:sin (90° – α) = cos (α)
余角余弦:cos (90° – α) = sin (α)
余角正切:tan (90° – α) = cotan (α)
余角的余割: cosec (90° – α) = sec (α)
余角正割:sec (90° – α) = cosec (α)
余角的余切:cotan (90° – α) = tan (α)
附加角度
补角(α 和β )的总和等于 180° 或 π 弧度,因此我们可以推导出公式 α + β = 180°。或者换句话说,如果 α 的补角为β ,则必须满足以下表达式β = 180 – α 。然后你可以看到我们可以从这些角度推断出的身份列表:
补角的正弦:sin (180° – α) = sin (α)
附加角的余弦:cos (180° – α) = -cos (α)
补角正切:tan (180° – α) = -tan (α)
附加角的余割: cosec (180° – α) = cosec (α)
补角正割:sec (180° – α) = -sec (α)
补角余切:cotan (180° – α) = -cotan (α)
共轭角
共轭角(α 和β )是那些总和等于 360° 或 2π 弧度的角,这就是为什么我们可以推导出公式 α + β = 360°。根据第一个公式,我们可以将其中一个角度用另一个角度表示如下:α = 360° – β或β = 360° – α。现在我们将向您展示共轭角的相等性:
共轭角的正弦:sin (360° – α) = – sin (α)
共轭角的余弦:cos (360° – α) = cos (α)
共轭角正切:tan (360° – α) = – tan (α)
共轭角的余割: cosec (360° – α) = – cosec (α)
共轭角的正割:sec (360° – α) = sec (α)
共轭角的余切:cotan (360° – α) = – cotan (α)
对角
对角或负角(α 和β )是具有相同数值但符号不同的角,此类角的示例为 30° 和 -30°。应该记住,负号表示顺时针旋转,而正号表示逆时针旋转。
对角的正弦:sin (-α) = – sin (α)
对角余弦:cos(-α) = cos(α)
对角正切: tan (-α) = – tan (α)
对角余割: cosec (-α) = – cosec (α)
对角正割:sec (-α) = sec (α)
对角余切:cotan (-α) = – cotan (α)
与 90° 不同的角度或正/负 π/2 的角度
相差 90° 的角度或角度加/减 π/2 (α 和β )是相差 90° 的角度。因此,它们可以表示为β – α = 90°,其中β比α大 90°。这些角度还有一系列与两个角度的三角比相关的公式。
与 90° 不同的角度的正弦:sin (90° + α) = cos (α)
与 90° 不同的角度的余弦: cos (90° + α) = -sin (α)
与 90° 不同的角度的正切: tan (90° + α) = – cotan (α)
与 90° 不同的角度的余割: cosec (90° + α) = sec (α)
与 90° 不同的角度的正割: sec (90° + α) = -cosec (α)
与 90° 不同的角度的余切: cotan (90° + α) = -cotan (α)
不同于 180° 的角度或正/负 π 的角度
正/负角 π (α 和β )相当于相差 180° 的角度。因此,它们可以使用以下公式表示: β – α = 180°,其中β 180° 大于α 。接下来,我们向您展示与这些角度的三角比相关的三角恒等式:
与 180° 不同的角度的正弦:sin (180° + α ) = -sin ( α )
与 180° 不同的角度的余弦: cos (180° + α ) = -cos ( α )
与 180° 不同的角度的正切: tan (180° + α ) = tan ( α )
与 180° 不同的角度的余割: cosec (180° + α ) = -cosec ( α )
与 180° 不同的角度的正割: sec (180° + α ) = -sec ( α )
与 180° 不同的角度的余切: cotan (180° + α ) = cotan ( α )
三角比的变换
最后,三角恒等式允许我们通过其他运算来表达一定的三角比。因此,如果我们有比率之和并且希望将其表示为乘积,则可以诉诸这些公式。不幸的是,虽然没有针对每个算术运算的表达式,但您只能从加法或减法到乘积,反之亦然。
将加法或减法转换为乘积
下面四个公式帮助我们计算三角函数的加法和减法:
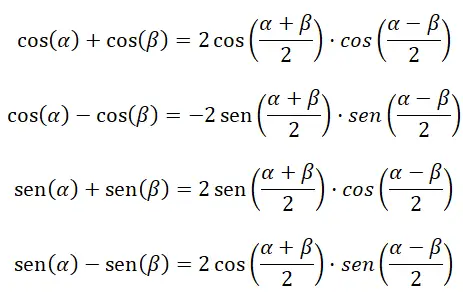
将乘积转化为加法或减法
以下四个公式帮助我们计算三角函数的乘积: