在此页面上,我们解释什么是三个向量的混合积(或三重点积)以及它的计算方法。您还将看到有关向量之间此类运算的示例、练习和已解决的问题。此外,您还会发现混合产品的特性和应用。
三个向量的混合积是多少?
三个向量的混合积,也称为三重点积,是三个向量之间的连续乘法,涉及两种不同类型的运算: 点积和向量积。因此,两个向量运算的组合给出一个标量(实数)。
具体地,混合乘积包括计算两个向量的向量乘积,并且随后将所获得的结果与第三向量相乘。这样写看起来可能很复杂,但实际上并没有那么复杂,看一下三点积公式:
![]()
正如您在其公式中看到的,三个向量的混合乘积由两个方括号表示。
如何计算三个向量的混合积?
三点积公式是我们在上一节中看到的公式,但是,它通常不用于确定三个向量的混合积,因为还有另一种更简单、更快的方法:
设任意 3 个向量为:
![]()
要计算三个向量之间的混合积,只需求解由向量分量形成的 3×3 行列式:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
所以你可以看一个如何计算的例子,我们将找到以下三个向量的混合乘积:
![]()
为了确定混合乘积,我们通过将向量放置在矩阵的行中来构造 3 阶行列式:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
现在我们只需要求解矩阵的行列式,为此你可以使用任何方法。在这种情况下,我们将应用 Sarrus 规则(但这也可以通过添加或辅助因子来完成):
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
为了证明这两个过程是等价的,我们将根据它们的定义来计算相同向量的混合积:
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
我们建议通过向量的行列式来计算混合乘积,因为它更快并且出错的机会更少。但是,正如您所看到的,无论您使用哪种方法,结果都是相同的,因此请使用您喜欢的方法。 👍
混合产品的几何解释
一旦您知道如何求三个向量的混合积,您可能会想……混合积的用途是什么?嗯,在数学中它有两个主要用途:计算平行六面体的体积和四面体的体积。
平行六面体的体积等于标记几何场的 3 个维度的向量的混合乘积的绝对值。
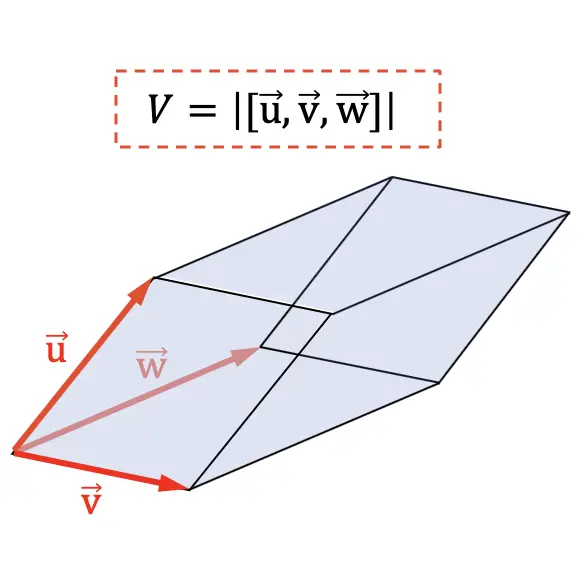
混合乘积的另一个应用是确定四面体的体积。因为在几何上,混合乘积绝对值的第六部分代表四面体的体积:
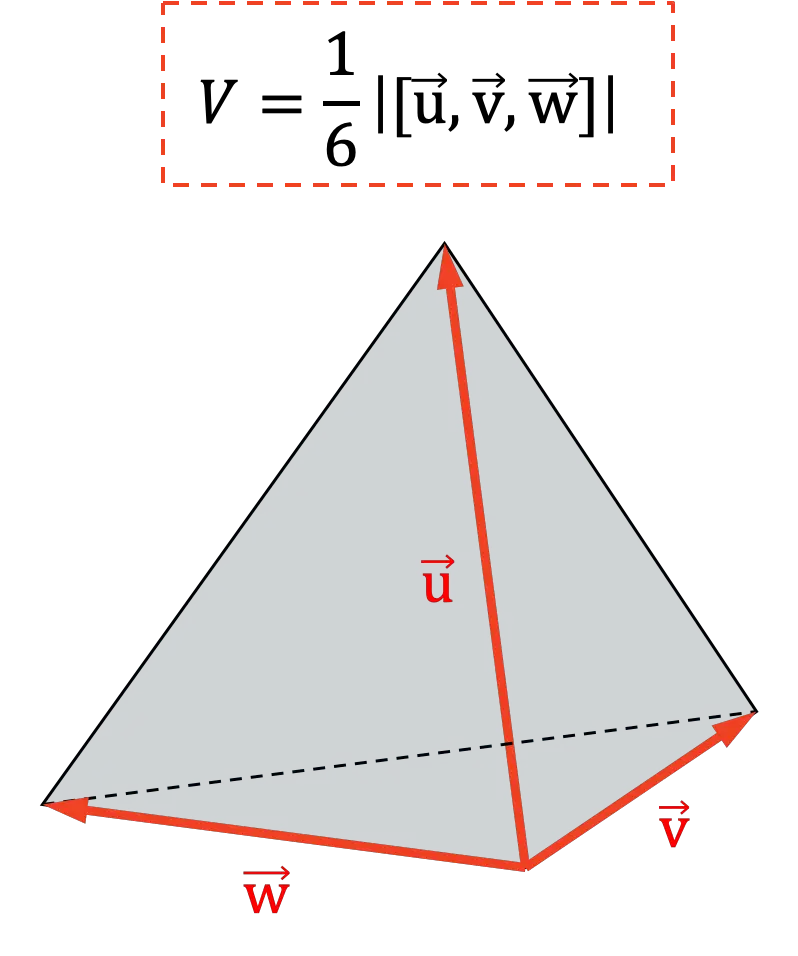
混合积或三点积的性质
混合乘积或三标量乘积具有以下特征:
- 一般来说,混合乘积向量顺序的变化也意味着符号的变化。因此,混合乘积向量的顺序很重要。
![]()
- 然而,如果我们循环改变顺序,符号不会改变:
![]()
- 在三维空间(R3 中)中,三个线性相关或共面向量(属于同一平面)的混合积等于 0。
修复了混合产品问题
练习1
给定 3 个向量:
![]()
计算三个向量的混合积:
![]()
为了找到它的混合积,我们必须求解由向量坐标组成的行列式:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
练习2
给定 3 个向量:
![]()
确定三个向量之间的混合积:
![]()
为了找到它的混合乘积,我们需要求解具有线性形式向量的笛卡尔坐标的行列式:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
练习3
计算 3 条边为以下向量的平行六面体的体积:
![]()
平行六面体的体积等于其作为边的 3 个向量的混合乘积的绝对值。因此,我们首先计算向量的三重叉积:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
这样平行六面体的体积就是混合乘积结果的绝对值:
![]()
练习4
计算顶点为以下点的四面体的体积:
![]()
首先,我们计算代表四面体边缘的向量:
![]()
![]()
![]()
四面体的体积等于其 3 个边向量的混合乘积绝对值的六分之一。因此,我们首先计算找到的向量的混合积:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
因此,四面体的体积将是混合乘积绝对值的六分之一:
![]()