在本页中,我们解释了酉矩阵是什么,此外,我们还通过几个练习对其进行了说明,以便更好地理解它。您还将发现这种类型的矩阵的所有属性对于线性代数如此重要。
什么是酉矩阵?
酉矩阵的定义如下:
因此,这个条件意味着单位矩阵的逆是其共轭转置,因为根据逆矩阵的定义,如果一个矩阵的乘积等于矩阵 d’identify,则该矩阵就是另一个矩阵的逆。
![Rendered by QuickLaTeX.com \left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8f035ef94e00b67acffd2881944642f_l3.png)
因此,酉矩阵将始终是正则矩阵或非简并矩阵,因为它始终具有逆矩阵。
另一方面,实数环境中酉矩阵的类似物是正交矩阵,在这种情况下,酉矩阵乘以其转置等于单位矩阵。
![]()
因此,在这种情况下,U 的逆矩阵将直接是其转置(或转置)矩阵。
单位矩阵示例
维度为 2×2 的单位矩阵示例
一旦我们了解了单位矩阵的概念,我们将通过一个 2×2 单位矩阵的示例来更好地理解它:
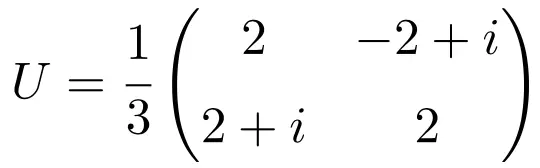
该矩阵是酉矩阵,因为其自身与其共轭矩阵相乘得到单位(或单位)矩阵:
![Rendered by QuickLaTeX.com \displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11df575022f8a50881fedc994f4f12af_l3.png)
而且,正如我们之前所看到的,任何酉矩阵都可以与其共轭转置交换:
![Rendered by QuickLaTeX.com \displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4848f3eab836be0996049e221bb8a8c3_l3.png)
单位对角矩阵示例
仅由复数i组成的对角矩阵也是酉矩阵的一个示例,与矩阵的维度无关。下面有一个已解决的练习,用尺寸为 3 × 3 的单位矩阵说明了这一点:
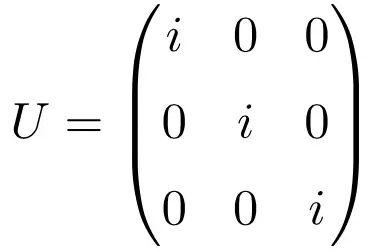
请注意,如果我们通过共轭转置求解矩阵的乘积,则会给出单位矩阵作为解:
![Rendered by QuickLaTeX.com \displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61bc73f95b9c2515595fe3ed2e18df3f_l3.png)
如果我们将矩阵反向相乘,也会发生同样的事情:
![Rendered by QuickLaTeX.com \displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cdf7b15d442ec89fde613ba2fd3fe45_l3.png)
这个矩阵的特点是它可以作为任意维度酉矩阵的一个例子,因为每次矩阵都是由主对角线上的虚数i构成,其余元素为零(0 )它将是一个酉矩阵。
酉矩阵的性质
单位矩阵的性质如下:
- 显然,任何酉矩阵都是正规矩阵。尽管并非所有正规矩阵都是酉矩阵。
- 酉矩阵始终是方阵。
- 所有单位矩阵都是可对角化的,即可以变换为对角矩阵。
- 单位矩阵的行列式的绝对值始终等于1。
![]()
- 相同的矩阵是酉矩阵。
- 对全部

,所有单位矩阵的集合
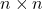
通过矩阵乘积运算,它们形成一个群,称为单位群。
- 使得两个同阶单位矩阵相乘得到另一个单位矩阵。
- 单位矩阵的所有特征值(或特征值)的模始终等于1。
![]()
- 此类矩阵的特征空间是正交的。